Biotensegrity
The mechanics of fascia
Introduction
Fascia is the fabric of the body; not the vestments covering the corpus, but the warp and weft of the material. The other tissues, muscle and bone, liver and lung, gut and urinary, brain and endocrine, are embroidered into the fascial fabric. Remove all other tissues from their fascial bed and the structure and form of the corpus remains, ghostlike, but clearly defined. The fascial system is a continuum, a structure that evolved hierarchically from the one cell embryo to the organism, and it is constantly adapting to new stresses to meet the structural demands of the organism (Guimberteau et al. 2007). Fascia without stiffeners would be as limp as a rag doll; remove the hydroxyapatite crystals from bone, and the form of bones remains, but soft, as if the starch has been removed from a stiff shirt. Wolff recognized that bone is stiffened in response to compression stress and what must happen is that the support structure of the body, the fascia with its enmeshed bony stiffeners, evolves in accordance to physical laws (Wolff & Wessinghage 1892).
Fascia is a tension network, with all the collagen inherently stressed, the so-called “pre-stress” of biologic tissues. Where does the compression arise? It is easy to see in an archer’s bow. The bowstring pulls the limbs of the bow towards the center belly of the bow, compressing it, and bending the bow into its characteristic shape. Now imagine the “bow” being compressed toward its belly by multiple bowstrings that encircle the bow and are all pulled at once. If the forces were balanced, the bow would not bend, but merely compress. Tension elements at each end that compress toward the center can balance to create a pure compression force, and in a tensioned fascial network bone will be laid down, according to Wolff’s law.
The origins of biotensegrity
For this to happen, there must be some evolutionary structural process that is governed by the rules of physics and influenced by the genome. In 1981, a structural model was proposed that incorporated the physical laws related to triangulated (and therefore inherently stable) structural forms, “closest packing”, and foams, and the “tensegrity” structures as conceived by Kenneth Snelson (Snelson 2009) and Buckminster Fuller (Fuller & Applewhite 1975) into a biologic model that would appropriately model organisms from viruses to vertebrates, their systems and subsystems: biotensegrity (Levin 1981). Biotensegrity reverses the centuries-old concept that the skeleton is the frame upon which the soft tissue is draped, and replaces it with an integrated fascial fabric with “floating” compression elements (bones in vertebrates), enmeshed within the interstices of the tensioned elements.
For a structure to be stable with flexible joints, it must be triangulated, as only triangles are stable with flexible joints. Biologic structures, their elements joined by surface tension, and flexible soft tissues, must be triangulated structures for them to exist. If not triangulated, it would require stiff joints, or constant, unobtainable, muscle forces to keep from collapsing. Of the three fully triangulated structures, the tetrahedron, octahedron and icosahedron, the icosahedron is the most suitable for biologic modeling. It has the largest volume for surface area, is omnidirectional, has the closest packing capabilities, and endo- and exoskeletal configurations, where the compression elements are either in its outer shell, or incorporated into the innards of the structure (Fig. 3.5.1). The internally vectored icosahedron is a tensegrity structure, simply defined as “floating compression” elements enmeshed in a continuous tension network. The compression elements are isolated from one another and the load is carried through the network, and not a compression-loaded “column of blocks”, governed by gravity-oriented levers, as is the norm in most familiar structures. The tensegrity icosahedron can be linked in an infinite array, hierarchically and as fractals (Mandelbrot 1982; see Fig. 3.5.2). It is a low-energy structure, using minimal materials to enclose space and give maximum strength. Because of triangulation, it has flexible joints but is stable and adaptable. Its mechanics are nonlinear, which is consistent with biologic materials and structures. Columns depend on gravity to hold them together; without gravity, columns and structures that depend on columns for support would fall apart. Tensegrities are self-contained structures and do not rely on gravity as a cohesive force. Table 3.5.1 compares biologic structure properties with the properties of standard, lever mechanics and tensegrity icosahedral mechanics.
Table 3.5.1
Comparison of properties of biologic systems, lever mechanics and tensegrity icosahedral mechanics
| Biologic systems | Lever systems | Tensegrity icosahedron |
| Nonlinear | Linear | Nonlinear |
| Global | Local | Global |
| Structurally continuous | Discontinuous | Structurally continuous |
| Gravity independent | Gravity dependent | Gravity independent |
| Omnidirectional | Unidirectional | Omnidirectional |
| Low energy | High energy | Low energy |
| Flexible joints | Rigid joints | Flexible joints |
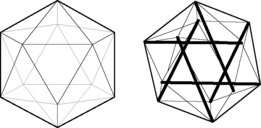
Fig. 3.5.1 • “Exoskeletal” icosahedron, with 20 triangulated faces, 12 vertices, 30 edges, and its “endoskeletal” icosahedron counterpart. In the endoskeletal icosahedron, the triangulated outer shell is under tension and the internalized compression struts are “floating” within the tension shell. The compression struts span to opposite vertices; they do not touch one another, and do not pass through the center of the icosahedron.
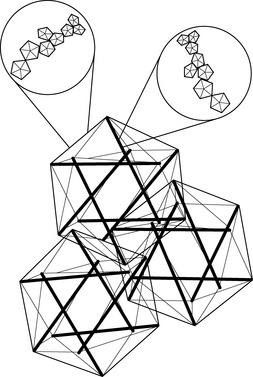
Fig. 3.5.2 • Hierarchical tensegrity icosahedrons. The pattern is repeated at every organizational level, from subcellular to organism.
It is obvious that lever systems, the standard for over three centuries, do not match the qualities needed for biologic modeling, and tensegrity icosahedral systems are a perfect match.
Like coins crowded together on a tabletop, bubbles in foam, cells in a beehive, biologic cells must conform and adjust to the pressures surrounding them. The individual cell must keep from being crushed by external forces. From the standpoint of efficiency and conservation of energy, crowded objects on a two-dimensional plane will pack closest as hexagons. Three-dimensional cells will conform to what has been known about foams for over 100 years; they will pack closest with three edges meeting at 120° and four edges meeting at a corner. Icosahedrons will pack closest around a central, smaller, icosahedron, following these rules. Fuller has described the closest packing of icosahedrons as the closest relationship of energy efficient, symmetrical, stable structures in three dimensions (Fuller & Applewhite 1975). In the past, cells were thought of as bags of fluid and the incompressibility of fluid kept them from being crushed. In the early 1930s, an internal cell skeleton (the cytoskeleton) was suspected, but it took another two decades to demonstrate it using the electron microscope. Ingber proposed that the cytoskeleton is a tensegrity structure with a mechanical structural framework to support cell integrity and he models these tensegrities as icosahedrons (Ingber et al. 1981). Following Wolff’s law, the cytoskeleton will align itself in such a way as to resist the crushing compressive load, and the rigid tubulin of the cytoskeleton becomes its “bones”. Levin proposed that the same mechanism created a hierarchical evolution of the musculoskeletal system, a hierarchical tensegrity (Levin 1982, 1986, 1988, 1990). Kroto, the Nobel Prize winner for his work on C60, the icosahedral form of carbon, demonstrates the self-organizing properties of icosahedrons into sphere-like structures and “icosaspirals”, helical structures of stacking icosahedrons (Kroto 1988). Icosahedrons and icosaspirals are ubiquitous in biologic structures, as demonstrated at every scale level: from 10−12 m (e.g., the fullerene molecule C60 and some amino acids) to 10−9 m (viruses, microtubules), to 10−6 m (red blood cells, pollen grains), to 10−4 m and 10−3 m (radiolarians), all the way up to organisms such as pufferfish at 10− 2 m, and greater. This hierarchy of structure development results in a fascial continuum, from subcellular to total organism.
Myofascia as the tensioner in the biotensegrity model
Central to this concept is the understanding that the fascia imparts a continuous tension to the system. Fascia displays the nonlinearity characteristic of all biologic tissues. In nonlinear tissues, the stress/strain relationship never reaches zero (a characteristic of linear materials); and there is always tension inherent in the system. It gives the “continuous tension”, an essential component of tensegrity, that helps set the tone of the organism. There are active contractile elements in fascia (Schleip et al. 2005) and the fascial network is intimately bound to muscle (Passerieux et al. 2007). Muscle also has intrinsic “tone” and is never completely lax, and the entire fascial network is continually tensed, by both intrinsic tension and active contractions that can be “tuned”. The mechanics of tensegrity structures are quite different than the lever mechanics that have been applied to biologic structures since Borelli’s treatise (Borelli 1680). Contrary to lever mechanics, hierarchical tensegrity structures have only tension and compression members. There is no shear or torque, nor are there bending moments. Orientation in space has no effect on how the structure functions. Forces are distributed throughout the system rather than locally concentrated as they are in lever systems. The system functions as a single unit. All this makes for a more energy efficient system. Movement is not bending of hinges, but expansion, repositioning and contraction of tensegrities. An instant repositioning of tensegrities allows for freely moving joints while the triangulation imparts stability of form and function. Biotensegrity is the unifying mechanical structural concept that bridges the islands of information that we now have about fascia and its role in body functions, and makes them a unified archipelago for understanding fascia’s role in anatomy and physiology.
Fascial training
The concept of biotensegrity not only offers a theoretical foundation to body mechanics and dynamics, it is also appropriate for establishing a concrete base to develop a process that can be seen as an internal fascial training. We propose mental motor imagery involving visual representation and kinesthetic awareness suggested by the principle of biotensegrity to support movement.
The stability of a tensegrity structure is due to the equilibrium between outward pushing of the rigid elements that tense the tension network, and inward pulling of the tension continuum that compresses the rigid elements without letting them touch each other: tensegrity structures can be seen as restrained expansion. Expansion (or space) creates tension. An increase of tension in a tensegrity structure lets it resist and become stronger. The training consists in using mental processes to generate a tangible feeling of the bones as space-makers and of the space between them. As a result, we can develop the perception of a tensional internal support. Once having found this internal support, it becomes possible to “relax” within it. “Relaxation”, far from being a simple “letting-go”, with its well-known effect of collapsing and weakening, is a redistribution of tension within the tensile fascial network with the qualities of space and strength, and a balance of tension. Space, tension, resistance, strength, internal support, and relaxation are concomitant, even equivalent, characteristics.
Poles of movement
A further step of the training is to include these qualities in movement. While moving a tensegrity structure, we can make several observations. To move it, we grasp it at its two ends (Fig. 3.5.3) and impart a rotational movement in them, one in relation to each other, or move one end, stabilizing the other, which creates a relative opposite movement of the stable end. Movement has an intrinsically polar quality and we call those areas where movement is initiated, “poles of movement”. Movement curves the structure, but the elements within respond by a new spatial organization without bending. Tension remains throughout the structure, on its concave side as well as on its convex side, and none of the rigid elements compress one another (Fig. 3.5.3). By focusing on the rotation of each pole separately, and letting each thumb follow a spiral whose direction is chosen to maintain tension on the concave side of the curve, we get a homogeneous curve, with all the elements involved relative to each other in a global movement (Fig. 3.5.3). If, instead, we focus on moving the poles toward each other in the space external to the structure, as is usually done in the movement instructions, the result will be an externally shorter distance between the poles and a sharp angle in the structure (Fig. 3.5.3). In this case, only a few elements of the structure have moved internally, the movement is local, and the tension is easily lost on the concave side.
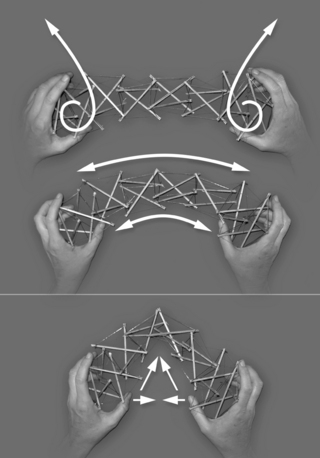
Fig. 3.5.3 • Taking a tensegrity structure at the poles of movement and rotating them following the spirals maintains tension throughout the structure, also on its concave side (thumbs side). The movement is evenly distributed, the curve homogeneous. Moving the poles while focusing on the distance between them results in an unevenly distributed movement with a sharp angle in the structure.
In the body, poles of movement can be the two bone ends building a joint, the tensegrity structure between being the interarticular space. Poles can also be chosen as any two remote bones, like two vertebrae, the intervening tensegrity structure the considered segment of the spine, or head and foot, the tensegrity structure between being the whole body.
We may move one pole of a chosen body part, following the spiral that helps to maintain the tension on the concave side, while maintaining the other pole stable. The cervical curve and its poles, the head (occiput) and the first thoracic vertebra, can be taken as an example. If, when flexing the head slightly, we maintain awareness of the occiput moving along a spiral line directed upward and posterior, (Fig. 3.5.4, upper bold spiral), it will prevent the head from “falling” forward and downward and it gives support to the front of the neck.

Fig. 3.5.4 • Possible poles of movement in the spine. The text refers to the two upper poles comprising the cervical curve. The upper pole (occiput) follows the bold spiral directed upward and posterior in flexion, and the dashed spiral upward and posterior in extension. The bold spirals show the direction of the spirals according to the global mobilization of the spinal curves out of their more or less rigid shape.
Integrating the myofascial–skeletal system
Although the movement is subtle, one can feel the underlying vertebrae being carried along through the activated tension network around the neck. Perhaps one can also feel this movement spread over the spine and the whole body, since the body parts with their poles are all interconnected, as shown in Fig. 3.5.4 for the spine. The movement is slight, slow, employing minimal muscular force, and one can relax in the internally supported structure. If one takes one vertebra after the other as a pole and moves them in turn in the described manner, a complete flexion of the curve is achieved. Each movement is slight, but every part moves. The movement is well distributed, occurring at every vertebral level, and the throat is not compressed. We can also change the direction and execute an extension following the dashed spiral (Fig. 3.5.4). Flexion moves the cervical curve evenly out of the lordosis, and extension moves it into the lordosis, but evenly and with the internal support that controls the movements that might disrupt the curve. This way, a body part that was rigid can be gently brought to life. If we now consider one joint the moving structure, awareness of the internal support, especially on the side of flexion, will prevent a closing or compression in the hollow of the curve.
In addition to the direction of movement given by the spiral, we also include the resisting quality of the tensioned elements. By training the kinesthetic perception of the subtle resistance that accompanies the movement (which is an adaptation from a mental technique used in a Chinese martial art), we enhance all the qualities already mentioned. It is also interesting to consider the resistance the result of two opposite movements: the movement actually performed and the counter-movement that slows it down. It is mentally challenging to perceive both simultaneously, but it is this training of the nervous system that results in a profound improvement of fluidity, strength, and elasticity of movement.
Summary
By internalizing these qualities, we can play with all the directions in space, connecting the spirals continuously in alternatively small or large movements, in slow or fast rhythms, which more overtly addresses the omnidirectionality of the fascial network, its elasticity, and its ability to react to different impulses such as stretch or vibration.
A characteristic of this training is the use of minimal muscular strength. Studies have shown that, whether a movement is mentally or physically performed, the nervous system tends to react similarly (Malouin et al. 2003) and muscle strength is developed (Ranganathan et al. 2004). It means that mental imagery allows us the use of muscular work in a remarkably economical manner to achieve optimal movement efficiency and ease.
With time, movements become naturally supported by the internalized principles of biotensegrity: the perception of internal space as well as the feeling of the ubiquitous tension that governs the mechanics of the body can lead to a maximal recruitment of the structure under optimally balanced tension. Consequently, movements become freer and more efficient, be it in movement disciplines, in daily activities, or in a therapeutic setting. An additional consequence of this approach to body structure and movement is to create a useful relationship to gravity. Instead of being a force that compresses our organism and makes us small and bent, gravity becomes a force that initiates space and strength in our structure.
References
Borelli G. De motu animalium. Apud Petrum Gosse; 1680.
Fuller R.B., Applewhite E.J. Synergetics: explorations in the geometry of thinking. New York: Macmillan; 1975.
Guimberteau J.C., Bakhach J., Panconi B., et al. A fresh look at vascularized flexor tendon transfers: concept, technical aspects and results. J. Plast. Reconstr. Aesthet. Surg.. 2007;60(7):793–810.
Ingber D.E., Madri J.A., Jamieson J.D. Role of basal lamina in neoplastic disorganization of tissue architecture. Proc. Natl. Acad. Sci. U. S. A.. 1981;78(6):3901–3905.
Kroto H. Space, stars, C60, and soot. Science. 1988;242(4882):1139–1145.
Levin S.M. The icosahedron as a biologic support system. 34th Annual Conference Alliance for Engineering in Medicine and Biology. Bethesda: Alliance for Engineering in Medicine and Biology; 1981:404. Houston
Levin S.M. The Ida P. Rolf Library of Structural Integration. Bulletin of Structural Integration. 1982;8(1):31–33.
Levin S.M. The icosahedron as the 3-D model for biological support. 30th Annual Meeting of the Society for General Systems Research. USA: Intersystems Publications; 1986:G14–G26.
Levin S.M. Space truss: A systems approach to cervical spine mechanics. IOP Publishing, San Antonio; 1988.
Levin S.M. The primordial structure. 34th Meeting of The International Society for the Systems Sciences. Pomona: International Society for the Systems Sciences; 1990:716–720. Portland,
Malouin F., Richards C.L., Jackson P.L., et al. Brain activations during motor imagery of locomotor-related tasks: a PET study. Hum. Brain Mapp.. 2003;19(1):47–62.
Mandelbrot B.B. The fractal geometry of nature. New York, NY: Freeman; 1982.
Passerieux E., Rossignol R., Letellier T., et al. Physical continuity of the perimysium from myofibers to tendons: involvement in lateral force transmission in skeletal muscle. J. Struct. Biol.. 2007;159(1):19–28.
Ranganathan V.K., Siemionow V., Liu J.Z., et al. From mental power to muscle power–gaining strength by using the mind. Neuropsychologia. 2004;42(7):944–956.
Schleip R., Klingler W., Lehmann-Horn F. Active fascial contractility: Fascia may be able to contract in a smooth muscle-like manner and thereby influence musculoskeletal dynamics. Med. Hypotheses. 2005;65(2):273–277.
Snelson K. Available from http://www.kennethsnelson.net, 2009. (accessed 10.08.11.)
Wolff J., Wessinghage D. Das Gesetz der Transformation der Knochen. Berlin: Hirschwald; 1892.