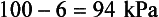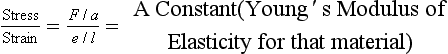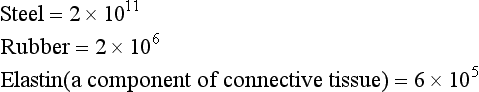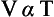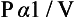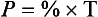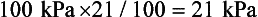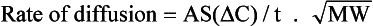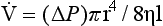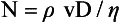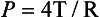SOME BASIC SCIENCE
States of matter
The matter in the world around us can be considered to be made up of particles (molecules) which exist in three states: solids, liquids and gases. The respiratory system involves all three.
In solids
The molecules are strongly attached to each other and are very tightly packed. Their movement within the solid is highly constrained. Very few molecules escape from the surface of a solid.
In liquids
The molecules are freer to move within the bulk of the liquid, and the most rapidly moving may escape into the space above the liquid to form a gas which exerts a vapour pressure. Molecules in a liquid are, however, quite powerfully attracted to each other and those on the surface of a liquid are attracted into the bulk of the liquid by those underneath. This effect forms a skin which has surface tension (Fig. A1).This is why drops of rain form spheres and drops of liquid on a surface that is not wetted by the liquid do not spread out to form a thin film. Of particular interest to us is the situation when a liquid forms a bubble or lines the tiny bubbles (alveoli) of the lungs (see Surface tension and bubbles below).
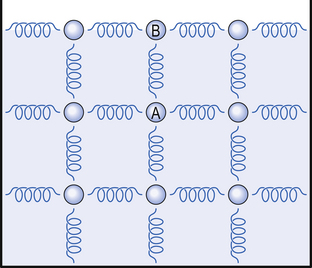
Fig. A1 The origin of surface tension. Molecules attract each other. In a liquid they have freedom to move in any direction within the bulk of the liquid. Molecule A is equally attracted in all directions so any slight imbalance will cause it to move. Molecule B, on the surface, is attracted only below and to the sides which retains it on the surface of the liquid. The forces in the horizontal plane give the surface tension like a sheet being pulled at all corners.
In gases
Molecules are free to move throughout the vessel containing them (they do this at considerable speed, molecules of room air are moving at about 500 ms−1, the speed of a respectable revolver bullet; we do not feel their impact because they are so light). Because they are so far apart, the attraction between gas molecules is relatively weak. The impact of these molecules on the walls of the vessel containing the gas exerts a pressure which depends on the temperature (which determines the velocity of the molecules) and the number of molecules present.
An interesting fact is that in a mixture of gases each of the constituents of the mixture behaves entirely independently of the other gases, it exerts its pressure as if the others were not there. This partial pressure that a particular gas in a mixture exerts is part of the total pressure exerted by the mixture and is numerically proportional to the amount of the gas present. For example it is intuitively obvious that in a cylinder containing only O2 (100% O2) 100% of the pressure is due to O2. It is not so obvious that in a cylinder containing, say, 25% O2, 25% of the total pressure, whatever that may be, is due to O2 (see Dalton’s Law, p. 155).
The molecules of a liquid that escape into the space above the liquid exert a partial pressure. This pressure is proportional to temperature because the higher the temperature the more molecules have enough energy to escape; but unlike the partial pressure of gases, this vapour pressure is independent of the total pressure over the liquid. This effect is particularly important in terms of the effects of water and volatile anaesthetics. Water at body temperature exerts a partial pressure of 6 kPa. That means within the lungs, where the air is saturated with water, if the atmospheric pressure is 100 kPa (about normal at sea level) there is only
remaining to be made up by the other gases of the atmosphere. This is no problem at sea level but when you go to altitude the temperature inside the lungs stays the same so water in the lungs still exerts 6 kPa but the total pressure falls so that the component due to water has a bigger effect (being unaffected by the total pressure). This is particularly important in terms of O2 supplies to the body. Similarly, the vapour of substances used as anaesthetics (e.g. chloroform) can exert partial pressures which dangerously reduce the pressure remaining to be occupied by O2.
Elasticity – and scarred lungs
One of the properties of solids which it is important, in understanding how the respiratory system works, is that of elasticity. The definition of an elastic material or object is one which returns to its original shape when a distorting force is removed. Perfectly elastic bodies obey Hook’s Law, that the force (F) applied to a body is directly proportional to its extension (x) (or compression).
An important concept is that energy is stored in a distorted elastic body and is released to return it to its original shape.
Stress is the force (F) per unit area (a) applied to the body (and has the units Nm−2).
Strain is the increase in length per unit length produced by a stress (as both increase in length (e) and unit length (l) have the same dimensions strain is dimensionless).
Hook’s Law can be expressed in a different way for a body made of a particular material:
Be careful not to confuse the terms elastic and elasticity. A material is said to be perfectly elastic if it gives up all the energy put into it by distorting forces to return to its original shape, without sequestering any as heat. A high modulus of elasticity on the other hand is frequently a property of materials that in everyday speech we do not usually refer to as elastic.
Thus Young’s Modulus (in Nm−2) for:
The highly elastic nature of steel is clearly seen if a steel ball is dropped on a steel plate. The ball returns to nearly the height from which it was dropped, showing it has given up almost all the kinetic energy which was used to distort it on impact with the plate in returning to its original shape. That is one of the reasons why the balls in the ‘Newton’s Cradle’ executive desk-top toy are made of steel not putty.
It is the elasticity of the respiratory system that brings about normal quiet expiration by restoring the lungs and chest wall to the end-expiratory position. This elasticity is reduced in fibrosing lung diseases where the lungs are scarred and stiff: this makes breathing more difficult. In emphysema elasticity changes to make the lungs more ‘floppy’, which causes them to collapse, trapping air in the lungs.
The gas laws
Just as the elastic properties of solids can be mathematically defined, the pressure volume and temperature of a fixed mass of gas are related with mathematical precision by what are known as the gas laws. It is these laws by which we measure loss of lung function in disease:
Charles’ Law. The volume (V) of a mass of gas at constant pressure varies directly with its absolute temperature:
Boyle’s Law. The pressure (P) of a mass of gas at constant temperature is inversely proportional to its volume (V):
These two laws can be combined to describe the relationship between pressure, temperature and volume of a mass of gas under different conditions. This is called The General Gas Equation:
where 1 and 2 are the two different conditions being considered.
The General Gas Equation is invaluable when we wish to take into account of what happens to the volume of inhaled cold air when it is warmed in the lungs. This correction is essential when measuring the amount of gas breathed in lung function tests (see Chapter 11) because the temperature and pressure at which the exhaled gas was measured will vary depending on the temperature of the room and the barometric pressure on that day. The temperature of the gas within the lungs, on the other hand, will be a fairly constant body temperature of 32°C. The general gas equation is also used when we wish to calculate what is happening in a plethysmograph (pp. 46, 145), which is an instrument used to record pattern of breathing.
Dalton’s Law of Partial Pressure. Each gas in a mixture of gases exerts the same pressure as it would if it alone occupied the same volume as the mixture. This is another way of saying that gases in a mixture have no effect on one another; they ‘ignore’ each other. Another way of expressing the partial pressure (P) of a gas which makes up a % of a mixture which exerts a total pressure (T) is:
Thus if the atmosphere exerts 100 kPa and contains 21% O2 the partial pressure of O2 is:
This law is absolutely fundamental to understanding the monitoring of patients in intensive care, patients being anaesthetised or in diagnosing many lung diseases. Composition of gases administered to patients and the composition of gases sampled from patients’ lungs is frequently reported in terms of partial pressures.
Graham’s Law of Diffusion. Describing the fact that lighter molecules travel faster than heavier ones, Graham’s Law states: the rates of diffusion (D) of two gases at the same temperature and pressure are inversely proportional to the square roots of their molecular weights (MW).
where 1 and 2 refer to the two gases.
Because the molecular weights of the three main gases in the air (O2, N2, and CO2) are about 32, 28 and 44 daltons respectively, their rates of diffusion in the gases in the alveoli of the lungs are not very different. This does not mean that the ease with which the respiratory gases are taken up and released by the blood is about the same because other factors are involved (see below).
Fick’s Law of Diffusion. The rate of diffusion of a substance through a membrane is proportional to the area of the membrane (A), the solubility (S) of the substance in the membrane, the concentration gradient ΔC, and inversely proportional to the thickness of the membrane (t) and the square root of the substance’s molecular weight:
Evolution has resulted in the lung exploiting Fick’s law by evolving a thin wall of large area between air and gas and a system of ventilation and perfusion that ensures a steep concentration gradient. Carbon dioxide is 23 times more soluble in tissue fluid than O2 and even though it has a greater molecular weight, it will diffuse 20 times more rapidly down the same concentration gradient. This is why, when the respiratory membrane across which diffusion takes place in the lungs is reduced or damaged by disease, uptake of O2 is usually impeded before loss of CO2.
Henry’s Law. This describes diffusion across a gas–liquid interface. It states that at equilibrium the amount of a gas dissolved in a given volume of the liquid at a given temperature is proportional to the partial pressure of that gas in the gas phase above the liquid.
The situation under physiological situations is slightly more complicated because, although the amount of a single gas dissolved is always proportional to its partial pressure, obeying Henry’s Law, different gases have different solubility coefficients and therefore different absolute amounts dissolve at the same partial pressure (more CO2 than O2 for example).
Also complicating the situation is the fact that a gas taken up in chemical combination with other substances in the solution is ‘locked away’ and not involved in the equilibrium, only that in free solution is considered. For example O2 must dissolve in blood plasma before it can reach its most important carrier in the blood haemoglobin. The solubility coefficient for O2 in blood without haemoglobin is very much lower than with haemoglobin. This storage phenomenon alters the amount carried. It does not alter the partial pressures involved and at equilibrium the partial pressure of a gas dissolved in a solution is the same as the partial pressure of the gas above the solution.
The flow of gases (which may be impeded in disease)
Flow of fluids (liquids and gases) takes place from a region of high pressure to a region of low pressure. During this flow pressure falls because energy is being used up in producing the flow. This using up of energy is the result of viscosity, which Sir Isaac Newton described as a ‘lack of slipperiness’ between concentric layers of the fluid. Flow can be generally considered as one of two types lamina or turbulent. In laminar flow the fluid moves parallel with the walls of the conducting tube in organized layers called laminae. The action is something like closing of an old fashioned telescope where the tubes slide one within the other. It is the sort of flow you see in a gently flowing river. The ‘lack of slipperiness’ means there is a resistance to flow which depends on the rate of flow (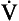
), the viscosity of the fluid (η) the length of the tube containing the fluid (l) and the radius of the tube (r).
Poiseuille’s Law states that in such a situation where the tube is relatively long and smooth a pressure difference (ΔP) between its ends will produce a flow-
This law strictly applies to straight circular rigid tubes of considerable length with smooth walls in which flow is constant. This does not apply to many tubes in the body. However, it makes a good approximation of what is happening under many circumstances, such as flow in the airways of the lungs and blood vessels and does not have the disadvantage of the intimidating mathematics associated with turbulent flow. This law is of outstanding importance to understanding what is happening to asthmatic patients where, during an attack, smooth muscle constricts their airways, reduces their radius and so has a profound effect on the air-flow through them.
Lamina flow becomes turbulent in the long straight smooth tube mentioned above when the flow exceeds a certain rate. In this perfect tube it is possible to calculate when this will happen by calculating Reynolds’ number (N):
where ρ is the density of the fluid, v is the velocity of flow and D is the diameter of the tube. When N exceeds 2000, flow is more likely than not to be turbulent.
Long straight round smooth tubes do not exist in the body and turbulent flow does occur. In turbulent flow a significant percentage of the movement of the fluid is not along the axis of the conducting tube, eddies take place with flow moving at all angles, even backward, against the general direction of flow. Turbulent flow is what you see in a rushing mountain stream. It is more difficult to propel a turbulent stream of fluid than a laminar one. If all other things are kept the same, to double a lamina flow you need to double the driving pressure; to double a turbulent flow you need to square the pressure. Turbulence is very important in causing particles to be deposited in the nose, and so protecting the lungs from pollution.
Surface tension and bubbles: why lungs tend to collapse in premature babies
The respiratory surfaces our lungs are moist – they are lined with a film of liquid which exhibits the properties of surface tension. The tubes and surfaces are curved (the major respiratory surface, the alveoli, are roughly spherical). This causes them to behave like bubbles. A bubble remains as a sphere because the air pressure inside it is greater than the pressure outside. This excess pressure resists the tendency of the bubble to collapse due to surface tension. In the case of a bubble, unlike the flat liquid surface considered in Figure A2, the attraction between the molecules is resolved in toward the centre of curvature.
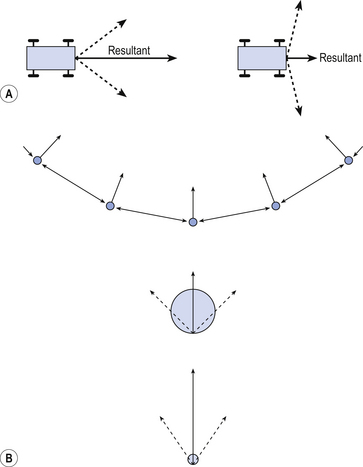
Fig. A2 Pressure in a bubble. If two people are pulling a cart with ropes (A), part of the tension in the ropes is exerted in the direction in which they want the cart to move. This is called the resultant of the two tensions or forces. The nearer they are to the required direction, the greater the effect (no-one would attempt to move something by pulling at right angles to the direction you want it to go). The same effect exists in a bubble (B) where the pull between molecules at its surface would cause the molecules to move in, collapsing the bubble if it was not for an excess pressure inside the bubble resisting the movement. You can see there is a bigger resultant (pressure) in a smaller bubble.
Laplace’s Law states that the pressure (P) inside a sphere of liquid of surface tension T is inversely proportional to the radius (R) of the sphere:
The excess pressure (P) inside a bubble is:
because there are two air/liquid surfaces to a bubble.
For a cylinder, like the airways of the lungs, where the surface only curves in one dimension and has only one air liquid surface:
The relationship between pressure and surface tension has important consequences for compliance of the lung (see Chapter 3) and is of particular importance in the treatment of premature babies whose lungs tend to collapse because they are not yet making sufficient of a surfactant which reduces surface tension.
Measuring gas volumes: to measure the extent of disease
The air around us is relatively cool and dry compared with the air in our lungs. From the laws we have listed we can expect the temperature and/or pressure of a volume of gas we inhale to change when it passes into the conditions inside our lungs. This creates difficulties when we are accurately measuring the size of a breath (it has a different volume before and after you have breathed it in than when it is inside you).
As with most measurements it doesn’t matter much which measuring system you use so long as you make it quite clear which you are using. The two most usual systems of expressing volume in respiratory physiology are: BTPS (Body Temperature and Pressure, Saturated with water vapour) which is the condition of air within the lungs or immediately leaving them; and STPD (Standard Temperature and Pressure Dry), which refers to the condition when the gas has all water vapour removed and is measured at 0°C (273° Kelvin) and 100 kPa (1 atmosphere, 1 bar, 760 mmHg). Although expressing the properties of a fixed amount of gas using these two systems would result in very different figures, this difference does not affect the systems described in this book. Therefore we do not mention it further except to repeat the warning that if you are carrying out quantitative measurements it is essential to specify what conditions the measurements were made under.
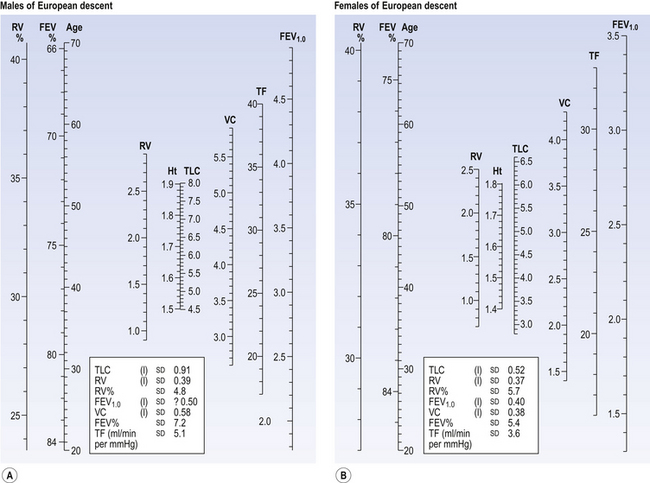
Fig. A3 Normograms. These have been constructed from considerable amounts of collected data and enable an estimate of a normal value of a lung variable by drawing a line from the age and height of the subject to the scale of the variable required. (A) Normal adult males of Western European descent. The RV% and the FEV% are related only to age and the TLC only to height. (B) Normal adult females. The RV% and the FEV% are related only to age.