Membrane Potentials and Action Potentials

Electrical potentials exist across the membranes of virtually all cells of the body. Some cells, such as nerve and muscle cells, generate rapidly changing electrochemical impulses at their membranes, and these impulses are used to transmit signals along the nerve or muscle membranes. In other types of cells, such as glandular cells, macrophages, and ciliated cells, local changes in membrane potentials also activate many of the cells' functions. This chapter reviews the basic mechanisms by which membrane potentials are generated at rest and during action by nerve and muscle cells.

Basic Physics of Membrane Potentials

Membrane Potentials Caused by Ion Concentration

Differences Across a Selectively Permeable Membrane

In Figure 5-1A, the potassium concentration is great inside a nerve fiber membrane but very low outside the membrane. Let us assume that the membrane in this instance is permeable to the potassium ions but not to any other ions. Because of the large potassium concentration gradient from inside toward outside, there is a strong tendency for extra numbers of potassium ions to diffuse outward through the membrane. As they do so, they carry positive electrical charges to the outside, thus creating electropositivity outside the membrane and electronegativity inside because of negative anions that remain behind and do not diffuse outward with the potassium. Within a millisecond or so, the potential difference between the inside and outside, called the diffusion potential, becomes great enough to block further net potassium diffusion to the exterior, despite the high potassium ion concentration gradient. In the normal mammalian nerve fiber, the potential difference is about 94 millivolts, with negativity inside the fiber membrane.

Figure 5-1 A, Establishment of a diffusion potential across a nerve fiber membrane, caused by diffusion of potassium ions from inside the cell to outside through a membrane that is selectively permeable only to potassium. B, Establishment of a diffusion potential when the nerve fiber membrane is permeable only to sodium ions. Note that the internal membrane potential is negative when potassium ions diffuse and positive when sodium ions diffuse because of opposite concentration gradients of these two ions.

Figure 5-1B shows the same phenomenon as in Figure 5-1A, but this time with a high concentration of sodium ions outside the membrane and a low concentration of sodium ions inside. These ions are also positively charged. This time, the membrane is highly permeable to the sodium ions but is impermeable to all other ions. Diffusion of the positively charged sodium ions to the inside creates a membrane potential of opposite polarity to that in Figure 5-1A, with negativity outside and positivity inside. Again, the membrane potential rises high enough within milliseconds to block further net diffusion of sodium ions to the inside; however, this time, in the mammalian nerve fiber, the potential is about 61 millivolts positive inside the fiber.

Thus, in both parts of Figure 5-1, we see that a concentration difference of ions across a selectively permeable membrane can, under appropriate conditions, create a membrane potential. Later in this chapter, we show that many of the rapid changes in membrane potentials observed during nerve and muscle impulse transmission result from the occurrence of such rapidly changing diffusion potentials.

The Nernst Equation Describes the Relation of Diffusion Potential to the Ion Concentration Difference Across a Membrane.

The diffusion potential level across a membrane that exactly opposes the net diffusion of a particular ion through the membrane is called the Nernst potential for that ion, a term that was introduced in Chapter 4. The magnitude of the Nernst potential is determined by the ratio of the concentrations of that specific ion on the two sides of the membrane. The greater this ratio, the greater the tendency for the ion to diffuse in one direction, and therefore the greater the Nernst potential required to prevent additional net diffusion. The following equation, called the Nernst equation, can be used to calculate the Nernst potential for any univalent ion at the normal body temperature of 98.6°F (37°C):

EMF (millivolts)=±61z×logConcentration insideConcentration outside

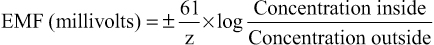
where EMF is electromotive force and z is the electrical charge of the ion (e.g., +1 for K⁺).

When using this formula, it is usually assumed that the potential in the extracellular fluid outside the membrane remains at zero potential, and the Nernst potential is the potential inside the membrane. Also, the sign of the potential is positive (+) if the ion diffusing from inside to outside is a negative ion, and it is negative (−) if the ion is positive. Thus, when the concentration of positive potassium ions on the inside is 10 times that on the outside, the log of 10 is 1, so the Nernst potential calculates to be −61 millivolts inside the membrane.

The Goldman Equation Is Used to Calculate the Diffusion Potential When the Membrane Is Permeable to Several Different Ions.

When a membrane is permeable to several different ions, the diffusion potential that develops depends on three factors: (1) the polarity of the electrical charge of each ion, (2) the permeability of the membrane (P) to each ion, and (3) the concentrations (C) of the respective ions on the inside (i) and outside (o) of the membrane. Thus, the following formula, called the Goldman equation or the Goldman-Hodgkin-Katz equation, gives the calculated membrane potential on the inside of the membrane when two univalent positive ions, sodium (Na⁺) and potassium (K⁺), and one univalent negative ion, chloride (Cl⁻), are involved.

EMF (millivolts)=−61×logCNai+PNa++CKi+PK++CCIo−PCI−CNao+PNa++CKo+PK++CCIi−PCI−

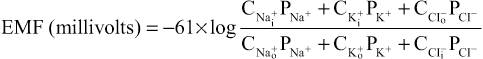
Several key points become evident from the Goldman equation. First, sodium, potassium, and chloride ions are the most important ions involved in the development of membrane potentials in nerve and muscle fibers, as well as in the neuronal cells in the nervous system. The concentration gradient of each of these ions across the membrane helps determine the voltage of the membrane potential.

Second, the quantitative importance of each of the ions in determining the voltage is proportional to the membrane permeability for that particular ion. That is, if the membrane has zero permeability to potassium and chloride ions, the membrane potential becomes entirely dominated by the concentration gradient of sodium ions alone, and the resulting potential will be equal to the Nernst potential for sodium. The same holds for each of the other two ions if the membrane should become selectively permeable for either one of them alone.

Third, a positive ion concentration gradient from inside the membrane to the outside causes electronegativity inside the membrane. The reason for this phenomenon is that excess positive ions diffuse to the outside when their concentration is higher inside than outside. This diffusion carries positive charges to the outside but leaves the nondiffusible negative anions on the inside, thus creating electronegativity on the inside. The opposite effect occurs when there is a gradient for a negative ion. That is, a chloride ion gradient from the outside to the inside causes negativity inside the cell because excess negatively charged chloride ions diffuse to the inside, while leaving the nondiffusible positive ions on the outside.

Fourth, as explained later, the permeability of the sodium and potassium channels undergoes rapid changes during transmission of a nerve impulse, whereas the permeability of the chloride channels does not change greatly during this process. Therefore, rapid changes in sodium and potassium permeability are primarily responsible for signal transmission in neurons, which is the subject of most of the remainder of this chapter.

Measuring the Membrane Potential

The method for measuring the membrane potential is simple in theory but often difficult in practice because of the small size of most of the fibers. Figure 5-2 shows a small pipette filled with an electrolyte solution. The pipette is impaled through the cell membrane to the interior of the fiber. Another electrode, called the “indifferent electrode,” is then placed in the extracellular fluid, and the potential difference between the inside and outside of the fiber is measured using an appropriate voltmeter. This voltmeter is a highly sophisticated electronic apparatus that is capable of measuring small voltages despite extremely high resistance to electrical flow through the tip of the micropipette, which has a lumen diameter usually less than 1 micrometer and a resistance more than a million ohms. For recording rapid changes in the membrane potential during transmission of nerve impulses, the microelectrode is connected to an oscilloscope, as explained later in the chapter.

Figure 5-2 Measurement of the membrane potential of the nerve fiber using a microelectrode.

The lower part of Figure 5-3 shows the electrical potential that is measured at each point in or near the nerve fiber membrane, beginning at the left side of the figure and passing to the right. As long as the electrode is outside the nerve membrane, the recorded potential is zero, which is the potential of the extracellular fluid. Then, as the recording electrode passes through the voltage change area at the cell membrane (called the electrical dipole layer), the potential decreases abruptly to −90 millivolts. Moving across the center of the fiber, the potential remains at a steady −90-millivolt level but reverses back to zero the instant it passes through the membrane on the opposite side of the fiber.

Figure 5-3 Distribution of positively and negatively charged ions in the extracellular fluid surrounding a nerve fiber and in the fluid inside the fiber. Note the alignment of negative charges along the inside surface of the membrane and positive charges along the outside surface. The lower panel displays the abrupt changes in membrane potential that occur at the membranes on the two sides of the fiber.

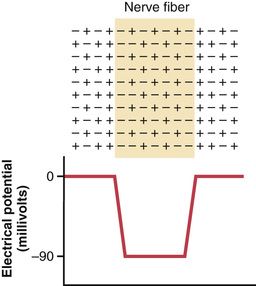
To create a negative potential inside the membrane, only enough positive ions to develop the electrical dipole layer at the membrane itself must be transported outward. All the remaining ions inside the nerve fiber can be both positive and negative, as shown in the upper panel of Figure 5-3. Therefore, transfer of an incredibly small number of ions through the membrane can establish the normal “resting potential” of −90 millivolts inside the nerve fiber, which means that only about 1/3,000,000 to 1/100,000,000 of the total positive charges inside the fiber must be transferred. Also, an equally small number of positive ions moving from outside to inside the fiber can reverse the potential from −90 millivolts to as much as +35 millivolts within as little as 1/10,000 of a second. Rapid shifting of ions in this manner causes the nerve signals discussed in subsequent sections of this chapter.

Resting Membrane Potential of Neurons

The resting membrane potential of large nerve fibers when they are not transmitting nerve signals is about −90 millivolts. That is, the potential inside the fiber is 90 millivolts more negative than the potential in the extracellular fluid on the outside of the fiber. In the next few paragraphs, the transport properties of the resting nerve membrane for sodium and potassium and the factors that determine the level of this resting potential are explained.

Active Transport of Sodium and Potassium Ions Through the Membrane—The Sodium-Potassium (Na⁺-K⁺) Pump.

Recall from Chapter 4 that all cell membranes of the body have a powerful Na⁺-K⁺ pump that continually transports sodium ions to the outside of the cell and potassium ions to the inside, as illustrated on the left side in Figure 5-4. Note that this is an electrogenic pump because more positive charges are pumped to the outside than to the inside (three Na⁺ ions to the outside for each two K⁺ ions to the inside), leaving a net deficit of positive ions on the inside and causing a negative potential inside the cell membrane.

Figure 5-4 Functional characteristics of the Na⁺-K⁺ pump and of the K⁺ “leak” channels. ADP, adenosine diphosphate; ATP, adenosine triphosphate. The K⁺ leak channels also leak Na⁺ ions into the cell slightly but are much more permeable to K⁺.

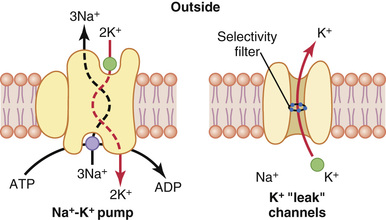
The Na⁺-K⁺ pump also causes large concentration gradients for sodium and potassium across the resting nerve membrane. These gradients are as follows:

Na+(outside) : 142 mEq/L

Na+(inside) : 14 mEq/L

K+(outside) : 4 mEq/L

K+(inside) : 140 mEq/L

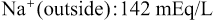
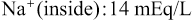
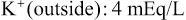
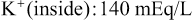
The ratios of these two respective ions from the inside to the outside are:

Na+inside/Na+outside=0.1

K+inside/K+outside=35.0

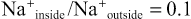
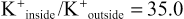
Leakage of Potassium Through the Nerve Cell Membrane.

The right side of Figure 5-4 shows a channel protein (sometimes called a tandem pore domain, potassium channel, or potassium [K⁺] “leak” channel) in the nerve membrane through which potassium can leak even in a resting cell. The basic structure of potassium channels was described in Chapter 4 (Figure 4-4). These K⁺ leak channels may also leak sodium ions slightly but are far more permeable to potassium than to sodium—normally about 100 times as permeable. As discussed later, this differential in permeability is a key factor in determining the level of the normal resting membrane potential.

Origin of the Normal Resting Membrane Potential

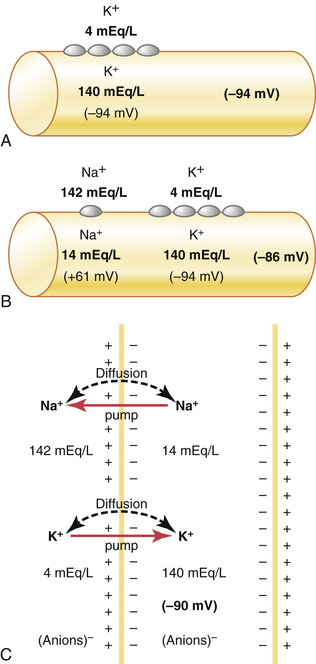
Figure 5-5 shows the important factors in the establishment of the normal resting membrane potential of −90 millivolts. They are as follows.

Figure 5-5 Establishment of resting membrane potentials in nerve fibers under three conditions: A, when the membrane potential is caused entirely by potassium diffusion alone; B, when the membrane potential is caused by diffusion of both sodium and potassium ions; and C, when the membrane potential is caused by diffusion of both sodium and potassium ions plus pumping of both these ions by the Na⁺-K⁺ pump.

Contribution of the Potassium Diffusion Potential.

In Figure 5-5A, we assume that the only movement of ions through the membrane is diffusion of potassium ions, as demonstrated by the open channels between the potassium symbols (K⁺) inside and outside the membrane. Because of the high ratio of potassium ions inside to outside, 35 : 1, the Nernst potential corresponding to this ratio is −94 millivolts because the logarithm of 35 is 1.54, and this multiplied by −61 millivolts is −94 millivolts. Therefore, if potassium ions were the only factor causing the resting potential, the resting potential inside the fiber would be equal to −94 millivolts, as shown in the figure.

Contribution of Sodium Diffusion Through the Nerve Membrane.

Figure 5-5B shows the addition of slight permeability of the nerve membrane to sodium ions, caused by the minute diffusion of sodium ions through the K⁺-Na⁺ leak channels. The ratio of sodium ions from inside to outside the membrane is 0.1, which gives a calculated Nernst potential for the inside of the membrane of +61 millivolts. Also shown in Figure 5-5B is the Nernst potential for potassium diffusion of −94 millivolts. How do these interact with each other, and what will be the summated potential? This question can be answered by using the Goldman equation described previously. Intuitively, one can see that if the membrane is highly permeable to potassium but only slightly permeable to sodium, it is logical that the diffusion of potassium contributes far more to the membrane potential than does the diffusion of sodium. In the normal nerve fiber, the permeability of the membrane to potassium is about 100 times as great as its permeability to sodium. Using this value in the Goldman equation gives a potential inside the membrane of −86 millivolts, which is near the potassium potential shown in the figure.

Contribution of the Na⁺-K⁺ Pump.

In Figure 5-5C, the Na⁺-K⁺ pump is shown to provide an additional contribution to the resting potential. This figure shows that continuous pumping of three sodium ions to the outside occurs for each two potassium ions pumped to the inside of the membrane. The pumping of more sodium ions to the outside than the potassium ions being pumped to the inside causes continual loss of positive charges from inside the membrane, creating an additional degree of negativity (about −4 millivolts additional) on the inside beyond that which can be accounted for by diffusion alone. Therefore, as shown in Figure 5-5C, the net membrane potential when all these factors are operative at the same time is about −90 millivolts.

In summary, the diffusion potentials alone caused by potassium and sodium diffusion would give a membrane potential of about −86 millivolts, with almost all of this being determined by potassium diffusion. An additional −4 millivolts is then contributed to the membrane potential by the continuously acting electrogenic Na⁺-K⁺ pump, giving a net membrane potential of −90 millivolts.

Neuron Action Potential

Nerve signals are transmitted by action potentials, which are rapid changes in the membrane potential that spread rapidly along the nerve fiber membrane. Each action potential begins with a sudden change from the normal resting negative membrane potential to a positive potential and ends with an almost equally rapid change back to the negative potential. To conduct a nerve signal, the action potential moves along the nerve fiber until it comes to the fiber's end.

The upper panel of Figure 5-6 shows the changes that occur at the membrane during the action potential, with the transfer of positive charges to the interior of the fiber at its onset and the return of positive charges to the exterior at its end. The lower panel shows graphically the successive changes in membrane potential over a few 10,000ths of a second, illustrating the explosive onset of the action potential and the almost equally rapid recovery.

Figure 5-6 Typical action potential recorded by the method shown in the upper panel of the figure.

The successive stages of the action potential are as follows.

Activation and Inactivation of the Voltage-Gated Sodium Channel

The upper panel of Figure 5-7 shows the voltage-gated sodium channel in three separate states. This channel has two gates—one near the outside of the channel called the activation gate, and another near the inside called the inactivation gate. The upper left of the figure depicts the state of these two gates in the normal resting membrane when the membrane potential is −90 millivolts. In this state, the activation gate is closed, which prevents any entry of sodium ions to the interior of the fiber through these sodium channels.

Figure 5-7 Characteristics of the voltage-gated sodium (top) and potassium (bottom) channels, showing successive activation and inactivation of the sodium channels and delayed activation of the potassium channels when the membrane potential is changed from the normal resting negative value to a positive value.

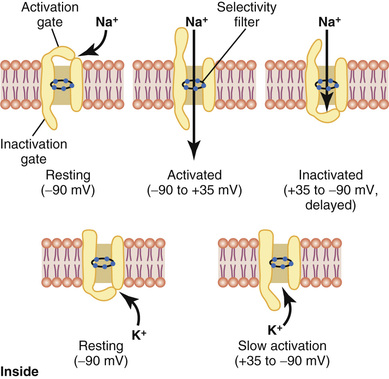
Activation of the Sodium Channel.

When the membrane potential becomes less negative than during the resting state, rising from −90 millivolts toward zero, it finally reaches a voltage—usually somewhere between −70 and −50 millivolts—that causes a sudden conformational change in the activation gate, flipping it all the way to the open position. During this activated state, sodium ions can pour inward through the channel, increasing the sodium permeability of the membrane as much as 500- to 5000-fold.

Inactivation of the Sodium Channel.

The upper right panel of Figure 5-7 shows a third state of the sodium channel. The same increase in voltage that opens the activation gate also closes the inactivation gate. The inactivation gate, however, closes a few 10,000ths of a second after the activation gate opens. That is, the conformational change that flips the inactivation gate to the closed state is a slower process than the conformational change that opens the activation gate. Therefore, after the sodium channel has remained open for a few 10,000ths of a second, the inactivation gate closes and sodium ions no longer can pour to the inside of the membrane. At this point, the membrane potential begins to return toward the resting membrane state, which is the repolarization process.

Another important characteristic of the sodium channel inactivation process is that the inactivation gate will not reopen until the membrane potential returns to or near the original resting membrane potential level. Therefore, it is usually not possible for the sodium channels to open again without first repolarizing the nerve fiber.

Voltage-Gated Potassium Channel and Its Activation

The lower panel of Figure 5-7 shows the voltage-gated potassium channel in two states: during the resting state (left) and toward the end of the action potential (right). During the resting state, the gate of the potassium channel is closed and potassium ions are prevented from passing through this channel to the exterior. When the membrane potential rises from −90 millivolts toward zero, this voltage change causes a conformational opening of the gate and allows increased potassium diffusion outward through the channel. However, because of the slight delay in opening of the potassium channels, for the most part, they open just at the same time that the sodium channels are beginning to close because of inactivation. Thus, the decrease in sodium entry to the cell and the simultaneous increase in potassium exit from the cell combine to speed the repolarization process, leading to full recovery of the resting membrane potential within another few 10,000ths of a second.

The “Voltage Clamp” Method for Measuring the Effect of Voltage on Opening and Closing of the Voltage-Gated Channels.

The original research that led to quantitative understanding of the sodium and potassium channels was so ingenious that it led to Nobel Prizes for the scientists responsible, Hodgkin and Huxley. The essence of these studies is shown in Figures 5-8 and 5-9.

Figure 5-8 The “voltage clamp” method for studying flow of ions through specific channels.

Figure 5-9 Typical changes in conductance of sodium and potassium ion channels when the membrane potential is suddenly increased from the normal resting value of −90 millivolts to a positive value of +10 millivolts for 2 milliseconds. This figure shows that the sodium channels open (activate) and then close (inactivate) before the end of the 2 milliseconds, whereas the potassium channels only open (activate), and the rate of opening is much slower than that of the sodium channels.

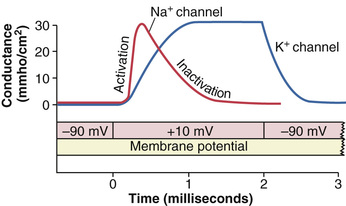
Figure 5-8 shows the voltage clamp method, which is used to measure the flow of ions through the different channels. In using this apparatus, two electrodes are inserted into the nerve fiber. One of these electrodes is used to measure the voltage of the membrane potential, and the other is used to conduct electrical current into or out of the nerve fiber. This apparatus is used in the following way: The investigator decides which voltage to establish inside the nerve fiber. The electronic portion of the apparatus is then adjusted to the desired voltage, automatically injecting either positive or negative electricity through the current electrode at whatever rate is required to hold the voltage, as measured by the voltage electrode, at the level set by the operator. When the membrane potential is suddenly increased by this voltage clamp from −90 millivolts to zero, the voltage-gated sodium and potassium channels open and sodium and potassium ions begin to pour through the channels. To counterbalance the effect of these ion movements on the desired setting of the intracellular voltage, electrical current is injected automatically through the current electrode of the voltage clamp to maintain the intracellular voltage at the required steady zero level. To achieve this level, the current injected must be equal to but of opposite polarity to the net current flow through the membrane channels. To measure how much current flow is occurring at each instant, the current electrode is connected to an oscilloscope that records the current flow, as demonstrated on the screen of the oscilloscope in Figure 5-8. Finally, the investigator adjusts the concentrations of the ions to other than normal levels both inside and outside the nerve fiber and repeats the study. This experiment can be performed easily when using large nerve fibers removed from some invertebrates, especially the giant squid axon, which in some cases is as large as 1 millimeter in diameter. When sodium is the only permeant ion in the solutions inside and outside the squid axon, the voltage clamp measures current flow only through the sodium channels. When potassium is the only permeant ion, current flow only through the potassium channels is measured.

Another means for studying the flow of ions through an individual type of channel is to block one type of channel at a time. For instance, the sodium channels can be blocked by a toxin called tetrodotoxin when it is applied to the outside of the cell membrane where the sodium activation gates are located. Conversely, tetraethylammonium ion blocks the potassium channels when it is applied to the interior of the nerve fiber.

Figure 5-9 shows typical changes in conductance of the voltage-gated sodium and potassium channels when the membrane potential is suddenly changed through use of the voltage clamp from −90 millivolts to +10 millivolts and then, 2 milliseconds later, back to −90 millivolts. Note the sudden opening of the sodium channels (the activation stage) within a small fraction of a millisecond after the membrane potential is increased to the positive value. However, during the next millisecond or so, the sodium channels automatically close (the inactivation stage).

Note the opening (activation) of the potassium channels, which open slowly and reach their full open state only after the sodium channels have almost completely closed. Further, once the potassium channels open, they remain open for the entire duration of the positive membrane potential and do not close again until after the membrane potential is decreased back to a negative value.

Summary of the Events that Cause the Action Potential

Figure 5-10 summarizes the sequential events that occur during and shortly after the action potential. The bottom of the figure shows the changes in membrane conductance for sodium and potassium ions. During the resting state, before the action potential begins, the conductance for potassium ions is 50 to 100 times as great as the conductance for sodium ions. This disparity is caused by much greater leakage of potassium ions than sodium ions through the leak channels. However, at the onset of the action potential, the sodium channels instantaneously become activated and allow up to a 5000-fold increase in sodium conductance. The inactivation process then closes the sodium channels within another fraction of a millisecond. The onset of the action potential also causes voltage gating of the potassium channels, causing them to begin opening more slowly a fraction of a millisecond after the sodium channels open. At the end of the action potential, the return of the membrane potential to the negative state causes the potassium channels to close back to their original status, but again, only after an additional millisecond or more delay.

Figure 5-10 Changes in sodium and potassium conductance during the course of the action potential. Sodium conductance increases several thousand–fold during the early stages of the action potential, whereas potassium conductance increases only about 30-fold during the latter stages of the action potential and for a short period thereafter. (These curves were constructed from theory presented in papers by Hodgkin and Huxley but transposed from squid axon to apply to the membrane potentials of large mammalian nerve fibers.)

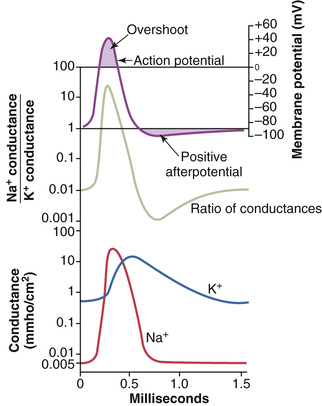
The middle portion of Figure 5-10 shows the ratio of sodium to potassium conductance at each instant during the action potential, and above this depiction is the action potential itself. During the early portion of the action potential, the ratio of sodium to potassium conductance increases more than 1000-fold. Therefore, far more sodium ions flow to the interior of the fiber than do potassium ions to the exterior. This is what causes the membrane potential to become positive at the action potential onset. Then the sodium channels begin to close and the potassium channels begin to open, and thus the ratio of conductance shifts far in favor of high potassium conductance but low sodium conductance. This shift allows very rapid loss of potassium ions to the exterior but virtually zero flow of sodium ions to the interior. Consequently, the action potential quickly returns to its baseline level.

Roles of Other Ions During the Action Potential

Thus far, we have considered only the roles of sodium and potassium ions in the generation of the action potential. At least two other types of ions must be considered: negative anions and calcium ions.

Impermeant Negatively Charged Ions (Anions) Inside the Nerve Axon.

Inside the axon are many negatively charged ions that cannot go through the membrane channels. They include the anions of protein molecules and of many organic phosphate compounds, sulfate compounds, and so forth. Because these ions cannot leave the interior of the axon, any deficit of positive ions inside the membrane leaves an excess of these impermeant negative anions. Therefore, these impermeant negative ions are responsible for the negative charge inside the fiber when there is a net deficit of positively charged potassium ions and other positive ions.

Calcium Ions.

The membranes of almost all cells of the body have a calcium pump similar to the sodium pump, and calcium serves along with (or instead of) sodium in some cells to cause most of the action potential. Like the sodium pump, the calcium pump transports calcium ions from the interior to the exterior of the cell membrane (or into the endoplasmic reticulum of the cell), creating a calcium ion gradient of about 10,000-fold. This process leaves an internal cell concentration of calcium ions of about 10⁻⁷ molar, in contrast to an external concentration of about 10⁻³ molar.

In addition, there are voltage-gated calcium channels. Because calcium ion concentration is more than 10,000 times greater in the extracellular fluid than in the intracellular fluid, there is a tremendous diffusion gradient for passive flow of calcium ions into the cells. These channels are slightly permeable to sodium ions and calcium ions, but their permeability to calcium is about 1000-fold greater than to sodium under normal physiological conditions. When the channels open in response to a stimulus that depolarizes the cell membrane, calcium ions flow to the interior of the cell.

A major function of the voltage-gated calcium ion channels is to contribute to the depolarizing phase on the action potential in some cells. The gating of calcium channels, however, is slow, requiring 10 to 20 times as long for activation as for the sodium channels. For this reason they are often called slow channels, in contrast to the sodium channels, which are called fast channels. Therefore, the opening of calcium channels provides a more sustained depolarization, whereas the sodium channels play a key role in initiating action potentials.

Calcium channels are numerous in both cardiac muscle and smooth muscle. In fact, in some types of smooth muscle, the fast sodium channels are hardly present; therefore, the action potentials are caused almost entirely by activation of slow calcium channels.

Increased Permeability of the Sodium Channels When There Is a Deficit of Calcium Ions.

The concentration of calcium ions in the extracellular fluid also has a profound effect on the voltage level at which the sodium channels become activated. When there is a deficit of calcium ions, the sodium channels become activated (opened) by a small increase of the membrane potential from its normal, very negative level. Therefore, the nerve fiber becomes highly excitable, sometimes discharging repetitively without provocation rather than remaining in the resting state. In fact, the calcium ion concentration needs to fall only 50 percent below normal before spontaneous discharge occurs in some peripheral nerves, often causing muscle “tetany.” Muscle tetany is sometimes lethal because of tetanic contraction of the respiratory muscles.

The probable way in which calcium ions affect the sodium channels is as follows: These ions appear to bind to the exterior surfaces of the sodium channel protein molecule. The positive charges of these calcium ions in turn alter the electrical state of the sodium channel protein, thus altering the voltage level required to open the sodium gate.

Initiation of the Action Potential

Up to this point, we have explained the changing sodium and potassium permeability of the membrane, as well as the development of the action potential, but we have not explained what initiates the action potential.

A Positive-Feedback Cycle Opens the Sodium Channels.

First, as long as the membrane of the nerve fiber remains undisturbed, no action potential occurs in the normal nerve. However, if any event causes enough initial rise in the membrane potential from −90 millivolts toward the zero level, the rising voltage will cause many voltage-gated sodium channels to begin opening. This occurrence allows rapid inflow of sodium ions, which causes a further rise in the membrane potential, thus opening still more voltage-gated sodium channels and allowing more streaming of sodium ions to the interior of the fiber. This process is a positive-feedback cycle that, once the feedback is strong enough, continues until all the voltage-gated sodium channels have become activated (opened). Then, within another fraction of a millisecond, the rising membrane potential causes closure of the sodium channels and opening of potassium channels, and the action potential soon terminates.

Threshold for Initiation of the Action Potential.

An action potential will not occur until the initial rise in membrane potential is great enough to create the positive feedback described in the preceding paragraph. This occurs when the number of sodium ions entering the fiber becomes greater than the number of potassium ions leaving the fiber. A sudden rise in membrane potential of 15 to 30 millivolts is usually required. Therefore, a sudden increase in the membrane potential in a large nerve fiber from −90 millivolts up to about −65 millivolts usually causes the explosive development of an action potential. This level of −65 millivolts is said to be the threshold for stimulation.

Propagation of the Action Potential

In the preceding paragraphs, we discussed the action potential as it occurs at one spot on the membrane. However, an action potential elicited at any one point on an excitable membrane usually excites adjacent portions of the membrane, resulting in propagation of the action potential along the membrane. This mechanism is demonstrated in Figure 5-11.

Figure 5-11 Propagation of action potentials in both directions along a conductive fiber.

Figure 5-11A shows a normal resting nerve fiber, and Figure 5-11B shows a nerve fiber that has been excited in its midportion—that is, the midportion suddenly develops increased permeability to sodium. The arrows show a “local circuit” of current flow from the depolarized areas of the membrane to the adjacent resting membrane areas. That is, positive electrical charges are carried by the inward-diffusing sodium ions through the depolarized membrane and then for several millimeters in both directions along the core of the axon. These positive charges increase the voltage for a distance of 1 to 3 millimeters inside the large myelinated fiber to above the threshold voltage value for initiating an action potential. Therefore, the sodium channels in these new areas immediately open, as shown in Figure 5-11C and D, and the explosive action potential spreads. These newly depolarized areas produce still more local circuits of current flow farther along the membrane, causing progressively more and more depolarization. Thus, the depolarization process travels along the entire length of the fiber. This transmission of the depolarization process along a nerve or muscle fiber is called a nerve or muscle impulse.

Direction of Propagation.

As demonstrated in Figure 5-11, an excitable membrane has no single direction of propagation, but the action potential travels in all directions away from the stimulus—even along all branches of a nerve fiber—until the entire membrane has become depolarized.

All-or-Nothing Principle.

Once an action potential has been elicited at any point on the membrane of a normal fiber, the depolarization process travels over the entire membrane if conditions are right, but it does not travel at all if conditions are not right. This principle is called the all-or-nothing principle, and it applies to all normal excitable tissues. Occasionally, the action potential reaches a point on the membrane at which it does not generate sufficient voltage to stimulate the next area of the membrane. When this situation occurs, the spread of depolarization stops. Therefore, for continued propagation of an impulse to occur, the ratio of action potential to threshold for excitation must at all times be greater than 1. This “greater than 1” requirement is called the safety factor for propagation.

Re-Establishing Sodium and Potassium Ionic Gradients After Action Potentials are Completed—Importance of Energy Metabolism

The transmission of each action potential along a nerve fiber reduces slightly the concentration differences of sodium and potassium inside and outside the membrane because sodium ions diffuse to the inside during depolarization and potassium ions diffuse to the outside during repolarization. For a single action potential, this effect is so minute that it cannot be measured. Indeed, 100,000 to 50 million impulses can be transmitted by large nerve fibers before the concentration differences reach the point that action potential conduction ceases. Even so, with time, it becomes necessary to re-establish the sodium and potassium membrane concentration differences, which is achieved by action of the Na⁺-K⁺ pump in the same way as described previously for the original establishment of the resting potential. That is, sodium ions that have diffused to the interior of the cell during the action potentials and potassium ions that have diffused to the exterior must be returned to their original state by the Na⁺-K⁺ pump. Because this pump requires energy for operation, this “recharging” of the nerve fiber is an active metabolic process, using energy derived from the adenosine triphosphate energy system of the cell. Figure 5-12 shows that the nerve fiber produces increased heat during recharging, which is a measure of energy expenditure when the nerve impulse frequency increases.

Figure 5-12 Heat production in a nerve fiber at rest and at progressively increasing rates of stimulation.

A special feature of the Na⁺-K⁺ adenosine triphosphatase pump is that its degree of activity is strongly stimulated when excess sodium ions accumulate inside the cell membrane. In fact, the pumping activity increases approximately in proportion to the third power of this intracellular sodium concentration. As the internal sodium concentration rises from 10 to 20 mEq/L, the activity of the pump does not merely double but increases about eightfold. Therefore, it is easy to understand how the “recharging” process of the nerve fiber can be set rapidly into motion whenever the concentration differences of sodium and potassium ions across the membrane begin to “run down.”

Plateau in Some Action Potentials

In some instances, the excited membrane does not repolarize immediately after depolarization; instead, the potential remains on a plateau near the peak of the spike potential for many milliseconds, and only then does repolarization begin. Such a plateau is shown in Figure 5-13; one can readily see that the plateau greatly prolongs the period of depolarization. This type of action potential occurs in heart muscle fibers, where the plateau lasts for as long as 0.2 to 0.3 second and causes contraction of heart muscle to last for this same long period.

Figure 5-13 Action potential (in millivolts) from a Purkinje fiber of the heart, showing a plateau.

The cause of the plateau is a combination of several factors. First, in heart muscle, two types of channels contribute to the depolarization process: (1) the usual voltage-activated sodium channels, called fast channels, and (2) voltage-activated calcium-sodium channels (L-type calcium channels), which are slow to open and therefore are called slow channels. Opening of fast channels causes the spike portion of the action potential, whereas the prolonged opening of the slow calcium-sodium channels mainly allows calcium ions to enter the fiber, which is largely responsible for the plateau portion of the action potential.

A second factor that may be partly responsible for the plateau is that the voltage-gated potassium channels are slower to open than usual, often not opening much until the end of the plateau. This factor delays the return of the membrane potential toward its normal negative value of −80 to −90 millivolts. The plateau ends when the calcium-sodium channels close and permeability to potassium ions increases.

Rhythmicity of Some Excitable Tissues—Repetitive Discharge

Repetitive self-induced discharges occur normally in the heart, in most smooth muscle, and in many of the neurons of the central nervous system. These rhythmical discharges cause (1) the rhythmical beat of the heart, (2) rhythmical peristalsis of the intestines, and (3) such neuronal events as the rhythmical control of breathing.

In addition, almost all other excitable tissues can discharge repetitively if the threshold for stimulation of the tissue cells is reduced to a low-enough level. For instance, even large nerve fibers and skeletal muscle fibers, which normally are highly stable, discharge repetitively when they are placed in a solution that contains the drug veratridine, which activates sodium ion channels, or when the calcium ion concentration decreases below a critical value, which increases sodium permeability of the membrane.

Re-excitation Process Necessary for Spontaneous Rhythmicity.

For spontaneous rhythmicity to occur, the membrane—even in its natural state—must be permeable enough to sodium ions (or to calcium and sodium ions through the slow calcium-sodium channels) to allow automatic membrane depolarization. Thus, Figure 5-14 shows that the “resting” membrane potential in the rhythmical control center of the heart is only −60 to −70 millivolts, which is not enough negative voltage to keep the sodium and calcium channels totally closed. Therefore, the following sequence occurs: (1) some sodium and calcium ions flow inward; (2) this activity increases the membrane voltage in the positive direction, which further increases membrane permeability; (3) still more ions flow inward; and (4) the permeability increases more, and so on, until an action potential is generated. Then, at the end of the action potential, the membrane repolarizes. After another delay of milliseconds or seconds, spontaneous excitability causes depolarization again and a new action potential occurs spontaneously. This cycle continues over and over and causes self-induced rhythmical excitation of the excitable tissue.

Figure 5-14 Rhythmical action potentials (in millivolts) similar to those recorded in the rhythmical control center of the heart. Note their relationship to potassium conductance and to the state of hyperpolarization.

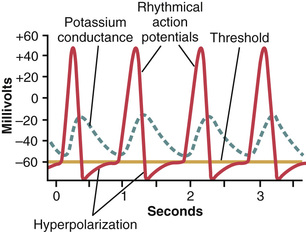
Why does the membrane of the heart control center not depolarize immediately after it has become repolarized, rather than delaying for nearly a second before the onset of the next action potential? The answer can be found by observing the curve labeled “potassium conductance” in Figure 5-14. This curve shows that toward the end of each action potential, and continuing for a short period thereafter, the membrane becomes more permeable to potassium ions. The increased outflow of potassium ions carries tremendous numbers of positive charges to the outside of the membrane, leaving considerably more negativity inside the fiber than would otherwise occur. This continues for nearly a second after the preceding action potential is over, thus drawing the membrane potential nearer to the potassium Nernst potential. This state, called hyperpolarization, is also shown in Figure 5-14. As long as this state exists, self–re-excitation will not occur. However, the increased potassium conductance (and the state of hyperpolarization) gradually disappears, as shown after each action potential is completed in the figure, thereby again allowing the membrane potential to increase up to the threshold for excitation. Then, suddenly, a new action potential results and the process occurs again and again.

Special Characteristics of Signal Transmission in Nerve Trunks

Myelinated and Unmyelinated Nerve Fibers.

Figure 5-15 shows a cross section of a typical small nerve, revealing many large nerve fibers that constitute most of the cross-sectional area. However, a more careful look reveals many more small fibers lying between the large ones. The large fibers are myelinated, and the small ones are unmyelinated. The average nerve trunk contains about twice as many unmyelinated fibers as myelinated fibers.

Figure 5-15 Cross section of a small nerve trunk containing both myelinated and unmyelinated fibers.

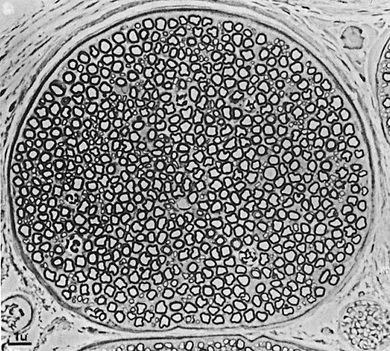
Figure 5-16 shows a typical myelinated fiber. The central core of the fiber is the axon, and the membrane of the axon is the membrane that actually conducts the action potential. The axon is filled in its center with axoplasm, which is a viscid intracellular fluid. Surrounding the axon is a myelin sheath that is often much thicker than the axon itself. About once every 1 to 3 millimeters along the length of the myelin sheath is a node of Ranvier.

Figure 5-16 Function of the Schwann cell to insulate nerve fibers. A, Wrapping of a Schwann cell membrane around a large axon to form the myelin sheath of the myelinated nerve fiber. B, Partial wrapping of the membrane and cytoplasm of a Schwann cell around multiple unmyelinated nerve fibers (shown in cross section). (A, Modified from Leeson TS, Leeson R: Histology. Philadelphia: WB Saunders, 1979.)

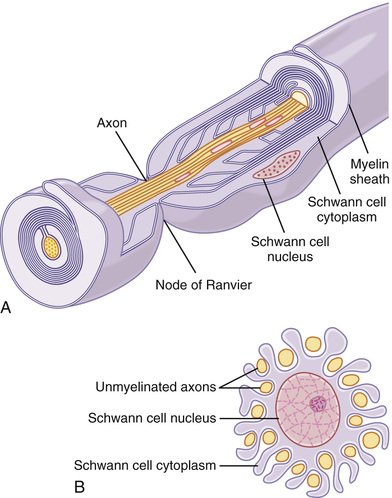
The myelin sheath is deposited around the axon by Schwann cells in the following manner: The membrane of a Schwann cell first envelops the axon. The Schwann cell then rotates around the axon many times, laying down multiple layers of Schwann cell membrane containing the lipid substance sphingomyelin. This substance is an excellent electrical insulator that decreases ion flow through the membrane about 5000-fold. At the juncture between each two successive Schwann cells along the axon, a small uninsulated area only 2 to 3 micrometers in length remains where ions still can flow with ease through the axon membrane between the extracellular fluid and the intracellular fluid inside the axon. This area is called the node of Ranvier.

“Saltatory” Conduction in Myelinated Fibers from Node to Node.

Even though almost no ions can flow through the thick myelin sheaths of myelinated nerves, they can flow with ease through the nodes of Ranvier. Therefore, action potentials occur only at the nodes. Yet the action potentials are conducted from node to node, as shown in Figure 5-17; this is called saltatory conduction. That is, electrical current flows through the surrounding extracellular fluid outside the myelin sheath, as well as through the axoplasm inside the axon from node to node, exciting successive nodes one after another. Thus, the nerve impulse jumps along the fiber, which is the origin of the term “saltatory.”

Figure 5-17 Saltatory conduction along a myelinated axon. The flow of electrical current from node to node is illustrated by the arrows.

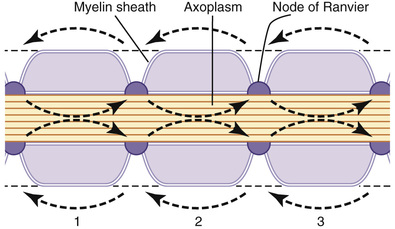
Saltatory conduction is of value for two reasons. First, by causing the depolarization process to jump long intervals along the axis of the nerve fiber, this mechanism increases the velocity of nerve transmission in myelinated fibers as much as 5- to 50-fold. Second, saltatory conduction conserves energy for the axon because only the nodes depolarize, allowing perhaps 100 times less loss of ions than would otherwise be necessary, and therefore requiring little energy expenditure for re-establishing the sodium and potassium concentration differences across the membrane after a series of nerve impulses.

The excellent insulation afforded by the myelin membrane and the 50-fold decrease in membrane capacitance also allow repolarization to occur with little transfer of ions.

Velocity of Conduction in Nerve Fibers.

The velocity of action potential conduction in nerve fibers varies from as little as 0.25 m/sec in small unmyelinated fibers to as great as 100 m/sec (more than the length of a football field in 1 second) in large myelinated fibers.

Excitation—The Process of Eliciting the Action Potential

Basically, any factor that causes sodium ions to begin to diffuse inward through the membrane in sufficient numbers can set off automatic regenerative opening of the sodium channels. This automatic regenerative opening can result from mechanical disturbance of the membrane, chemical effects on the membrane, or passage of electricity through the membrane. All these approaches are used at different points in the body to elicit nerve or muscle action potentials: mechanical pressure to excite sensory nerve endings in the skin, chemical neurotransmitters to transmit signals from one neuron to the next in the brain, and electrical current to transmit signals between successive muscle cells in the heart and intestine. For the purpose of understanding the excitation process, let us begin by discussing the principles of electrical stimulation.

Excitation of a Nerve Fiber by a Negatively Charged Metal Electrode.

The usual means for exciting a nerve or muscle in the experimental laboratory is to apply electricity to the nerve or muscle surface through two small electrodes, one of which is negatively charged and the other positively charged. When electricity is applied in this manner, the excitable membrane becomes stimulated at the negative electrode.

This effect occurs for the following reason: Remember that the action potential is initiated by the opening of voltage-gated sodium channels. Further, these channels are opened by a decrease in the normal resting electrical voltage across the membrane—that is, negative current from the electrode decreases the voltage on the outside of the membrane to a negative value nearer to the voltage of the negative potential inside the fiber. This effect decreases the electrical voltage across the membrane and allows the sodium channels to open, resulting in an action potential. Conversely, at the positive electrode, the injection of positive charges on the outside of the nerve membrane heightens the voltage difference across the membrane rather than lessening it. This effect causes a state of hyperpolarization, which actually decreases the excitability of the fiber rather than causing an action potential.

Threshold for Excitation and “Acute Local Potentials.”

A weak negative electrical stimulus may not be able to excite a fiber. However, when the voltage of the stimulus is increased, there comes a point at which excitation does take place. Figure 5-18 shows the effects of successively applied stimuli of progressing strength. A weak stimulus at point A causes the membrane potential to change from −90 to −85 millivolts, but this change is not sufficient for the automatic regenerative processes of the action potential to develop. At point B, the stimulus is greater, but the intensity is still not enough. The stimulus does, however, disturb the membrane potential locally for as long as 1 millisecond or more after both of these weak stimuli. These local potential changes are called acute local potentials, and when they fail to elicit an action potential, they are called acute subthreshold potentials.

Figure 5-18 Effect of stimuli of increasing voltages to elicit an action potential. Note development of acute subthreshold potentials when the stimuli are below the threshold value required for eliciting an action potential.

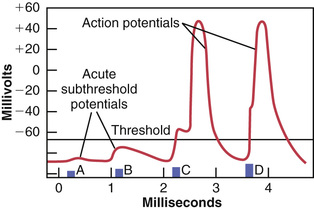
At point C in Figure 5-18, the stimulus is even stronger. Now the local potential has barely reached the level required to elicit an action potential, called the threshold level, but this occurs only after a short “latent period.” At point D, the stimulus is still stronger, the acute local potential is also stronger, and the action potential occurs after less of a latent period.

Thus, this figure shows that even a weak stimulus causes a local potential change at the membrane, but the intensity of the local potential must rise to a threshold level before the action potential is set off.

“Refractory Period” After an Action Potential, During Which a New Stimulus Cannot be Elicited

A new action potential cannot occur in an excitable fiber as long as the membrane is still depolarized from the preceding action potential. The reason for this restriction is that shortly after the action potential is initiated, the sodium channels (or calcium channels, or both) become inactivated and no amount of excitatory signal applied to these channels at this point will open the inactivation gates. The only condition that will allow them to reopen is for the membrane potential to return to or near the original resting membrane potential level. Then, within another small fraction of a second, the inactivation gates of the channels open and a new action potential can be initiated.

The period during which a second action potential cannot be elicited, even with a strong stimulus, is called the absolute refractory period. This period for large myelinated nerve fibers is about 1/2500 second. Therefore, one can readily calculate that such a fiber can transmit a maximum of about 2500 impulses per second.

Inhibition of Excitability—“Stabilizers” and Local Anesthetics

In contrast to the factors that increase nerve excitability, still others, called membrane-stabilizing factors, can decrease excitability. For instance, a high extracellular fluid calcium ion concentration decreases membrane permeability to sodium ions and simultaneously reduces excitability. Therefore, calcium ions are said to be a “stabilizer.”

Local Anesthetics.

Among the most important stabilizers are the many substances used clinically as local anesthetics, including procaine and tetracaine. Most of these substances act directly on the activation gates of the sodium channels, making it much more difficult for these gates to open, thereby reducing membrane excitability. When excitability has been reduced so low that the ratio of action potential strength to excitability threshold (called the “safety factor”) is reduced below 1.0, nerve impulses fail to pass along the anesthetized nerves.