Chapter 2
pH, EMF and Redox Potentials
Hydrogen ion concentrations are determined over a very wide range and, to avoid the inconvenience of using very small numbers, Sorenson introduced the concept of pH in 1909. He defined pH as the negative logarithm of the hydrogen ion concentration, viz:
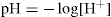
A similar notation can be applied to hydroxyl ion concentrations:
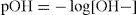
where [H+] and [OH–] represent the concentrations of hydrogen and hydroxyl ions, respectively.
On thermodynamic grounds these relationships are often modified to:
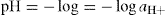
where aH+ and aOH – are the ‘activity’ or effective concentrations of hydrogen and hydroxyl ions, respectively. However, for dilute solutions, one can usually assume:
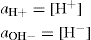
The pH scale nominally covers the range 0–14 but it is possible, under special circumstances, to have pH values outside these limits. A neutral solution has a pH of 7; acid solutions have pH values less than 7 and alkaline solutions greater than 7.
Ionization Constants
Strong acids and bases are, for all practical purposes, completely ionized in aqueous solution so that it is not possible to write any equilibrium expressions. For weak electrolytes, however, equilibrium expressions can be written and, by applying the Law of Mass Action, values of Ka or Kb can be calculated. Ionization constants, often loosely referred to as dissociation constants, are usually expressed in terms of pKa or pKb where pKa = –log Ka and pKb = –log Kb. Low values of pKa or high values of pKb are characteristic of relatively strong acids or weak bases, whereas high values of pKa or low values of pKb indicate relatively weak acids or strong bases. The Lowry Bronsted theory (details of which are outside the scope of this volume) enables the ionization constants of acids, bases and their salts to be verified on the pKa scale by using the expression:
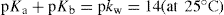
Ionization constants vary with temperature, and for purposes of comparison it is essential to record pKa values at the same temperature.
The acid dissociation constant (pKa value) of an ionizable compound is defined as the pH value at which the dissociated and undissociated species are of equal equilibrium concentration, i.e. pKa of a molecule is the pH at which the molecule is 50 per cent protonated. It is a fundamental physicochemical property that strongly influences many properties; for example, the neutral form of the compound is less water soluble and more lipophilic, and possesses higher membrane permeability than the ionized form. Experimental knowledge of compound pKa value provides a measure of the extent of compound ionization across the pH range of pharmaceutical relevance and is highly beneficial for predicting compound absorption, distribution, metabolism and excretion (ADME) properties. The pKa value also plays an important role in the development of drug delivery formulations. ‘pKa affects solubility, permeability, log D and oral absorption by modulating the distribution of neutral and charged species.’
Dissociation constants are important physicochemical parameters of a substance, and the knowledge of these parameters is of fundamental importance in a wide range of applications and research areas.
Applications of Dissociation Constant
The acid–base property of a drug molecule is the key parameter for drug development because it governs solubility, absorption, distribution, metabolism and elimination. Particularly for developing new APIs, the pKa has become of great importance because the transport of drugs into cells and across other membranes is a function of physicochemical properties and of the pKa of the drugs (Andrasi et al., 2007).
Knowledge of pKa values is important for the quantitative behaviour of systems involving acid–base equilibria in solution. Many applications exist in biochemistry; for example, the pKa values of proteins and amino acid side chains are of major importance for the activity of enzymes and the stability of proteins (Onufriev et al., 2001).
Buffer solutions are used extensively to provide solutions at or near the physiological pH for the study of biochemical reactions (Good et al., 1966); the design of these solutions depends on the knowledge of the pKa values of their components. There are many buffers available, which provide a solution with an optimum pH, which is used in different process, e.g. MOPS—a buffer used to maintain pH in gel electrophoresis.
The isoelectric point of a given molecule is a function of its pKa values, so different molecules have different isoelectric points. This phenomenon develops a technique called isoelectric focusing, which is used for separation of proteins by 2D gel polyacrylamide gel electrophoresis (PAGE).
In acid–base extraction, the efficiency of extraction of a compound into an organic phase, such as ether, can be optimized by adjusting the pH of the aqueous phase using an appropriate buffer. At the optimum pH, the concentration of the electrically neutral species is maximized; such a species is more soluble in organic solvents having a low dielectric constant than it is in water. This technique is used for the purification of weak acids and bases (Eyal et al., 1997).
In pharmacology, ionization of a compound alters its physical behaviour and macro properties such as solubility and lipophilicity (log p). For example, ionization of any compound will increase its solubility in water but decrease the lipophilicity. This is exploited in drug (it includes drug discovery/product development, preclinical research [microorganisms/animals] and clinical trials [on humans]) development to increase the concentration of a compound in the blood by adjusting the pKa of an ionizable group (Avdeef et al., 2003).
Knowledge of pKa values is important for the understanding of coordination complexes, which are formed by the interaction of a metal ion, Mm+, acting as a Lewis acid, with a ligand, L, acting as a Lewis base. However, the ligand may also undergo protonation reactions, so the formation of a complex in aqueous solution could be represented symbolically by the reaction
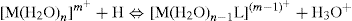
To determine the equilibrium constant for this reaction, in which the ligand loses a proton, the pKa of the protonated ligand must be known. In practice, the ligand may be polyprotic, e.g. EDTA–4 can accept four protons; in that case, all pKa values must be known. In addition, the metal ion is subjected to hydrolysis, that is, it behaves as a weak acid, so the pKa values for the hydrolysis reactions must also be known (Beck et al., 1990).
Assessing the hazard associated with an acid or base may require knowledge of pKa values (Van Leeuwen et al., 1995). For example, hydrogen cyanide is a very toxic gas, because the cyanide ion inhibits the iron-containing enzyme cytochrome c oxidase. Hydrogen cyanide is a weak acid in aqueous solution with a pKa of about 9. In strongly alkaline solutions, above pH 11, say, it follows that sodium cyanide is ‘fully dissociated’ so the hazard due to the hydrogen cyanide gas is much reduced. An acidic solution, on the other hand, is very hazardous because all the cyanide is in its acid form.
The chromatographic retention and electrophoretic behaviour of ionizable compounds strongly depend on the pKa of the compound and the mobile phase pH. Therefore, a satisfactory knowledge of the acid–base behaviour of substances in a hydro– organic media such as methanol (MeOH)/water is essential to predict the influence of pH on selectivity and retention in liquid chromatography (LC), and also to optimize analytical procedures for the separation of ionizable compounds by various techniques.
Most of drugs are weak organic acids or bases, existing in unionized and ionized forms in an aqueous environment. The unionized form is usually lipid soluble (lipophilic) and diffuses readily across cell membranes. The ionized form has low lipid solubility (but high water solubility—i.e. hydrophilic) and high electrical resistance and thus cannot penetrate cell membranes easily. The proportion of the unionized form present (and thus the drug’s ability to cross a membrane) is determined by the pH and the drug’s pKa (acid dissociation constant). The pKa is the pH at which concentrations of ionized and unionized forms are equal. When the pH is lower than the pKa, the unionized form of a weak acid predominates, and the ionized form of a weak base is predominated. Thus, in plasma (pH 7.4), the ratio of unionized to ionized forms for a weak acid (e.g. with a pKa of 4.4) is 1:1000; in gastric fluid (pH 1.4), the ratio is reversed (1000:1). Therefore, when a weak acid is given orally, most of the drug in the stomach is unionized, favouring diffusion through the gastric mucosa. For a weak base with a pKa of 4.4, the outcome is reversed; most of the drug in the stomach is ionized. Theoretically, weakly acidic drugs (e.g. aspirin) are more readily absorbed from an acid medium (stomach) than are weakly basic drugs (e.g. guanidine). However, whether a drug is acidic or basic, most absorption occurs in the small intestine because the surface area is larger and membranes are more permeable.
There are some conditions for weak acid and base drug, where ionization depends on the value of pH.
Determination of Dissociation Constant
Many potential drugs are weak acids or bases; therefore, one of the most important determinations carried out prior to development is the pKa or ionization constant. Strong acids are generally ionizable at all pH values, while the ionization of weak acid depends on pH value of the media. For example, HCl is strong acid and it ionizes at all pH values, whereas the ionization of a weakly acidic drug like salicylic acid is pH dependent. It is useful to know the extent to which the molecule is ionized at a certain pH because most of the physiochemical properties and biological properties such as solubility, stability, drug absorption and their activity are affected by degree of ionization of drug.
Determination of this parameter is, however, based on the Bronsted and Lowry theory of acids and bases. This states that an acid is a substance that can donate a hydrogen ion, and a base is one that can accept a proton.
The following equilibrium represents for a weak acid:
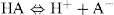(2.1)
The value of pKa of any substances cannot be determined by the theory given by Bronsted and Lowry, however, the equation given by Henderson–Hasselbach is the fulfilment to determination of dissociation constant. This equation relates the pKa to the pH of the solution and the relative concentrations of the dissociated and undissociated parts of a weak acid:
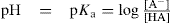(2.2)
where [A−] is the concentration of the dissociated species, and [HA] is the concentration of the undissociated species. This equation can be rearranged into Eq. 2.2 to yield the percentage of a compound that will be ionized at any particular pH.
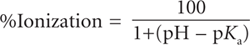(2.3)
A condition in Eq. 2.2, if 50 per cent dissociation (or ionization) occur then pKa = pH. It should also be noted that, usually, pKa values are preferred for bases instead of pKb values (pKw = pKa + pKb).
There are some significant approximations implicit in the Henderson–Hasselbalch equation. The most significant is the hypothesis that the concentration of the acid and its conjugate base at equilibrium will remain the same as the formal concentration. This neglects the dissociation of the acid and the hydrolysis of the base, and the dissociation of water itself is neglected. These approximations will fail when dealing with relatively strong acids or bases (pKa more than a couple units away from 7), dilute or very concentrated solutions (less than 1mm or greater than 1M) or heavily skewed acid–base ratios (more than 100:1). Also, the equation does not take into effect the dilution factor of the acid and conjugate base in water. If the proportion of acid to base is 1, then the pH of the solution will be different if the amount of water changes from 1mL to 1L.
The measurement of pKa is very difficult if a compound is hydrophobic in nature. It can be solved by measuring the apparent pKa of the compound in solvent and water mixtures and then extrapolating the data back to a purely aqueous medium using a Yasuda–Shedlovsky plot. The organic solvents most frequently used are methanol, ethanol, propanol, dimethylsulphoxide (DMSO), dimethylformamide (DMFA), acetone and tetrahydrofuran (THF). However, methanol is by far the most popular because its properties are closest to water. For example, ibuprofen and quinine have poor water solubility and determination of the pKas of ibuprofen and quinine in a range of organic solvent–water mixtures has been carried out by Avdeef et al. (1999). In case of the compound that contains an ultraviolet (UV) chromophore that changes with the extent of ionization, then a method involving UV spectroscopy can be used. This method involves measuring the UV spectrum of the compound as a function of pH. Mathematical analysis of the spectral shifts can then be used to determine the pKa(s) of the compound. This method is most suitable for compounds in which the ionizing group is closed to or actually within an aromatic ring, which usually results in large UV shifts upon ionization.
There are some techniques by which one can determine the ionization constant; these include the following:
Among these techniques, the potentiometric titration is the least time consuming, particularly for pKa determination as well as this technique is accurate and has good reproducibility. In addition, UV–Vis absorption spectrometry has still been used widely for the determination of dissociation constants, because of their accuracy and different pKa values of polyprotic substances to be determined, even when they have very close reproducibility. The UV method requires only 1mg of compound, and the potentiometric method requires 3mg of compound. In the last decade, some alternative techniques have been developed, based on separation methods such as liquid chromatography (LC) and capillary zone electrophoresis (CZE). The determination of pKa value by liquid chromatography is based on the relationship between the capacity factors and the pH values of the mobile phase. In addition, pKa values in water predicted by the SPARC online calculator have been investigated. The programme estimates the pKa values of any organic compound solely from its chemical structure (Hilal et al., 1996).
The conductimetric method for determining ionization constants requires knowledge of the degree of ionization which can be calculated from the formula:
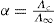
where Λ∞ is the equivalent conductance at infinite dilution and is a measure of the complete dissociation of the solute into its ions and Λc is the equivalent conductance of the solution being examined and is a measure of the number of solute particles present as ions at concentration c. The ratio Λc/ Λ∞ is known as the conductance ratio. To obtain Ka it is now necessary to substitute in the equation:
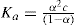
where c is the concentration.
Potentiometric Titration
In the past, potentiometric titration was the standard method for pKa measurement. In a potentiometric titration, a sample is titrated with acid or base using a pH electrode to monitor the course of titration. The pKa value is calculated from the change in shape of the titration curve compared with that of blank titration without a sample present. Analysis methods commonly used to derive pKas from titration curves include Gran’s plot (Andrasi et al., 2007), second derivative (Δ2pH/ΔV2) (Qiang et al., 2004), and least squares nonlinear regression. Potentiometric titration is a high-precision technique for determining the pKa values of substances. It is commonly used because of its accuracy and the commercial availability of fast, automated instruments. However, its shortcomings include the requirements to use a milligram of pure compounds and a mixture of aqueous buffers.
The potentiometric determination of ionization constants involves the titration of the acid or base and application of the Henderson equation:
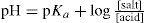
or
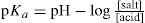
There are certain limitations in the use of this equation which need not concern us here but it is of interest to note that at 50 per cent neutralization, i.e. when [salt] = [acid] then pKa = pH. This means that the ionization constant can be read directly from a titration curve simply by recording the pH at 50 per cent neutralization.
Capillary Zone Electrophoresis (CE)
The determination of pKa values by capillary zone electrophoresis (CE) is based on observation of the effective mobility of an ionizable compound in a series of electrolyte solutions of constant ionic strength and various pHs. In its uncharged state, a solute has zero mobility while its fully ionized state has maximum mobility. The effective electrophoretic mobility of weak acids and bases is strongly influenced by environmental factors that affect underlying equilibrium constants (e.g. pH, ionic strength and temperature) as well as variables that affect ion mobility (e.g. ionic strength, temperature and viscosity). Electrolyte solutions of a different pH with a low and constant ionic strength as well as effective column thermostatting are therefore required for pKa measurements. Desirable buffer properties for the measurement of pKa values by CE include detector compatibility (usually low UV absorbing), reasonable water solubility, acceptable shelf life and availability in a high-purity form. The most popular buffers for CE are phosphate, acetate, borate and zwitterionic compounds (Good’s buffers). Intermediate mobility is therefore a function of dissociation equilibrium. The CE technique is expected to be especially useful if the amount of compound is very limited because, with this technique, only a few nanograms or less are commonly used for analysis. For CE, it is only necessary to determine pH-dependent mobilities, and that has several advantages. Over the past decade, capillary electrophoresis (CE) has emerged as a valuable tool for the evaluation of compound pKa values, as it possesses many favourable qualities (Evagelou et al., 2003; Sandra et al., 2007):
• Potential impurities and degradants can be separated from the target compound.
• Intimate knowledge of sample concentration is not required for analysis.
• Sparingly soluble compounds with a suitable UV chromophore can be analyzed.
• No changes in spectral properties are required for detection of a pKa value.
• Minimal sample amounts are required for analysis (μg amounts).
UV–Vis Spectrophotometric Methods
An alternative to potentiometric titration is UV–Vis spectrophotometry because it can handle compounds with lower solubility and lower sample concentrations. The main advantage is higher sensitivity (>10–6 M) to compounds with favourable molar absorption coefficients. However, in such a case, a compound must contain a UV-active chromophore close enough to the site of the acid–base function in the molecule. Spectral data are recorded continuously during the course of titration by a diode-array spectrometer. The absorption spectra of the sample changes during the course of the titration to reflect the concentration of neutral and ionized species present. The largest change in absorbance occurs at the pH corresponding to a pKa value. These changes are usually identified from the first derivative of the absorbance against time plot or from overlay plots of the different spectra. The determination of pKa values by UV–Vis assumes that the solute of interest is pure or that its impurities do not absorb in the UV–Vis range, since the spectra of impurities can overlap with those corresponding to the solutes of interest. Spectrophotometric methods offer excellent precision, as in potentiometry, but they require different spectra for different species and reagents must be pure. Traditionally, spectral data at a single analytical wavelength are acquired from a sample in a series of buffer solutions with known pH values, after which the pKa is determined. To use this method, the absorption spectra of individual species must be characterized earlier and the molar absorptivities of protonated and deprotonated species are thus required. These measurements are nontrivial if acid–base equilibria comprise more than two ionization steps or if reacting components are not stable within two pH units of the pKa value, so a multiwavelength spectrophotometric approach has been developed to determine acid dissociation. Target-factor analysis has been applied to deduce pKa values from the multiwavelength UV absorption data recorded at different pH values (Evagelou et al., 2003; Jimenez-Lozano et al., 2002).
NMR titration: NMR–pH titration is also an excellent technique for determining pKa values as the protonation of a basic site leads to electronic deshielding effects on the adjacent NMR-active nuclei, so the average chemical shifts of all the measurable NMR-active nuclei, as a function of pH, are expected to reflect the fractional protonation of each basic group of a molecule. The online coupling of a potentiometric titrator with an NMR spectrometer results in a powerful hyphenated technique called NMR controlled titration (Andrasi et al., 2007; Szakacs et al., 2004).
Liquid chromatography: The determination of pKa values by means of liquid chromatography (LC) is based on the relationships between capacity factors, and the pH of the mobile phase. LC is used as a powerful technique for the determination of dissociation constants, as it requires only a small quantity of compounds; studied samples do not need to be pure, and poor water solubility is not a serious drawback. This method does not include measuring solute or titrant concentrations, just retention times. Also, calculation is straightforward and independent of solute purity. However, the standard deviations of pKa values are higher than those obtained by potentiometric or spectrophotometric methods. One of the most important disadvantages of the LC method is that the pH of the mobile phase and, therefore, the range of pKa values that can be determined are limited by the stability of the column package. Moreover, due to the large retention times observed, it is not easy to determine pKa values in water and aqueous–organic mixtures with low contents of organic solvent. Nevertheless, as the main objective of pKa determination by LC is the optimization of chromatographic separations, this method is perfectly adequate for this purpose (Beltran et al., 2003; Erdemgil et al., 2007; Evagelou et al., 2003).
Combined Methods
In recent years, a new procedure has been developed when LC and CE methodologies are used for pKa determination in combination with a diode-array detector (DAD) for absorbance measurements. In these cases, pKa values can be determined from the absorbance spectra obtained at the maxima of chromatographic or electrophoretic peaks. That way, pKa values may be obtained from two independent methods: mobility/pH data and spectra/pH data in CE procedures (CE-DAD), and capacity factor/pH data and spectra/pH data in LC procedures (LC-DAD). The advantages of these proposed methods lie in the fact that the application of both methods does not increase the analysis time and enables the confirmation of results. Dissociation constants are also easy to determine by the LC-MS technique. The use of CE-MS provides high sensitivity as well as high selectivity, thereby ensuring that impurities that might interfere with compounds are not detected (Sandra et al., 2007).
Computational Methods
Theoretical pKa values can be calculated by computational methods (e.g. SPARC and ACD/Lab. SPARC is an online calculator that estimates the macroscopic and microscopic pKa of any organic compound solely from its chemical structure. ACD/pKa DB is a software program that calculates accurate acid–base ionization constants (pKa values) under 25ºC and zero ionic strength in aqueous solutions for almost any organic structure (Sandra et al., 2007).
pKa Determination in Nonaqueous Media
For substances sparingly soluble in water, aqueous–organic solvent mixtures are used to estimate their pKa values. The dissociation of uncharged substances in aqueous–organic mixtures is ruled by electrostatic interactions as well as specific solute–solvent interactions (solvation effects). In order to estimate aqueous pKa values, several experiments at different organic solvent concentrations should be performed. Aqueous pKa values that estimate by an extrapolation procedure (e.g. the Yasuda– Shedolovsky method) can be used to deduce the pKa values at zero organic solvent composition. The selected organic solvents are usually alcohols because they are amphiprotic and neutral solvents, and they show great ability to dissolve ionizable compounds. Then, the specific solute–solvent interactions should not be too different from those established in water. However, not all compounds dissolve in a single-component organic solvent–water mixture, so recently, a new, multicomponent, co-solvent mixture, comprising equal volumes of methanol, dioxane and acetonitrile, and referred to as MDM, has been found to be efficient for pKa measurement of various APIs. The application of MDM–water mixtures improves the solubility of poorly water-soluble APIs, so their pKa values can be measured in a lower proportion of organic solvent. The use of water–organic mixtures requires the correct measurement of pH in these media. Measurements are performed using IUPAC standardization rules (Sandra et al., 2007).
Table 2.1 pKa values of some important compounds |
|
| Compound | pKa |
| Salicylic acid | 3.0 |
| Benzoic acid | 4.2 |
| Sulphathiazole | 7.3 |
| Phenobarbitol | 7.4 |
| Metoprolol | 9.44± 0.1 |
| Formic acid | 3.75 |
| Trichloroacetic acid | 0.66 |
| Trifluoroacetic acid | 0.52 |
| Dichloroacetic acid | 1.35 |
| Flouroacetic acid | 2.59 |
| Acetic acid | 4.76 |
| Acetylsalicyclic | 3.49 |
| Ascorbic | 4.3, 11.8 |
| Boric acid | 9.24 |
| Penicillin V | 2.73 |
| Phenytoin | 8.1 |
| Sulphathiazole | 7.12 |
| Paracetamol | 9.5 |
| Penicillin G (Benzylpenicillin) | 3.42 |
| Ampicillin | 2.55± 0.01 |
| Acebutolol | 9.21 |
| Alprenolol | 9.38± 0.1 |
| Atenolol | 9.48± 0.01 |
| Ciprofloxacin | 6.42 |
| Danofloxacin | 6.07± 0.06; 8.56± 0.07 |
| Difloxacin 5.66± 0.04; 7.24± 0.06 | |
| Enoxacin | 6.00; 8.50 |
| Enrofloxacin | 5.88± 0.03; 7.74± 0.03 |
| Fleroxacin | 5.46; 8.00 |
| Flumequine | 6.35± 0.01 |
| Lomefloxacin | 5.00± 0.10; 6.25± 0.05; 9.00± 0.03 |
| Marbofloxacin | 5.69± 0.10; 8.02± 0.20 |
| Nalidixic acid | 5.95 |
| Fleroxacin | 5.46; 8.00 |
| Norfloxacine | 6.22; 8.38 |
| Pefloxacin | 6.21± 0.12; 7.87± 0.10 |
| Pipemidic acid | 5.42± 0.05; 8.18± 0.09 |
| Ofloxacin | 6.22± 0.05; 7.81 ±0.08 |
| Sarafloxacin | 5.62± 0.08; 8.18± 0.09 |
| Azithromycin | 7.34 |
| Clarithromycin | 7.25 |
| Erythromycin | 8.90± 0.15 |
| Roxithromycin | 9.17± 0.30 |
| Tylosin | 3.31± 0.30; 7.50± 0.13 |
| Amoxicillin | 3.39, 6.71; 9.41 |
| Phenobarbitol | 7.4 |
| Ammonia | 4.76 |
| Labetalol | 7.35 |
| Oxprenolol | 9.62 |
| Pindolol | 9.16 |
| Practolol | 9.41 |
| Propranolol | 9.49± 0.2 |
| Sotalol | 9.01 |
| Timolol | 9.34 |
| Metoprolol | 9.44± 0.1 |
| Omeprazole | 4.14; 8.90 |
| Butibufen | 4.64 |
| Carprofen | 4.63 |
| Diclofenac | 4.16 |
| Fenbufen | 4.56 |
| Flurbiprofen | 4.35 |
| Ibuprofen | 4.42± 0.08 |
| Piperazine | 5.33; 9.73 |
| Procaine | 2.28± 0.08; 9.02± 0.01 |
| Sulphacetamide | <2.5; 5.27 |
| Sulphachloropyridazine | 1.87± 0.30; 5.45± 0.06 |
| Sulphamerazine | 2.22± 0.01; 6.80± 0.01 |
| Sulphamethazine | 2.37± 0.01; 7.49± 0.01 |
| Atropine | 4.35 |
| Caffeine | 10.4, 13.4 |
| Codeine | 5.8 |
| Erythromycin | 5.2 |
| Morphine | 6.13 |
| Pilocarpine | 7.2, 12.7 |
| Quinine | 6.0, 9.89 |
| Tolbutamide | 8.7 |
| Cocain | 8.6 |
| Diazepam | 3.3 |
| Diphenhydramine | 9.0 |
| Morphine | 8.0 (amine) 9.9 (phenol) |
| Adrenaline (epinephrine) | 8.7 (amine), 10.2, 12.0 (phenols) |
| Sulphadiazine | 6.43 |
| Sulphadimethoxine | 2.13± 0.30; 6.08± 0.09 |
| Sulphaguanidine | 1.55; 11,24 |
| Chlortetracycline | 3.33± 0.30; 7.55± 0.02 |
| Demeclocycline | 3.37± 0.30; 7.36± 0.03 |
| Doxycycline | 3.02± 0.30; 7.97± 0.15 |
| Meclocycline | 4.05± 0.30; 6.87± 0.39 |
| Oxytetracycline | 3.04; 8.00 |
| Tetracycline | 3.32± 0.30; 7.78± 0.05; 9.58± 0.30 |
Buffer Solutions
Buffer solutions are usually solutions of weak acids (or bases) and their corresponding salts, e.g. acetic acid and sodium acetate. Such solutions resist changes of pH upon the addition of small quantities of acid or alkali and this phenomenon is known as buffer action. In solutions where the buffer action is absent or very low, the pH can change considerably due to the absorption of carbon dioxide from the air or extraction of alkali from the material of the glass container. In the example quoted above, the addition of a small quantity of strong acid (e.g. HCl) results in only a small decrease in pH because the hydrogen ions react with the sodium acetate to liberate the very much weaker acetic acid according to the reaction:
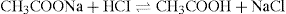
This equation can be expressed more generally as:
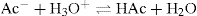
If a strong base (e.g. NaOH) is added to the buffer solution, the acetic acid neutralizes the hydroxyl ions:
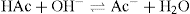
Buffer solutions are not usually prepared from weak bases and their salts since not only are many bases volatile but the solutions often have high temperature coefficients.
The pH of a buffer solution can be determined by applying the Henderson equation. If the salt and acid concentrations are known together with the pKa of the acid concerned then the pH may be calculated.
Example: What is the pH of the buffer solution prepared by mixing 5ml N/100 acetic acid (pKa 4.76) with 15ml N/10 sodium acetate?
Total volume = 20ml
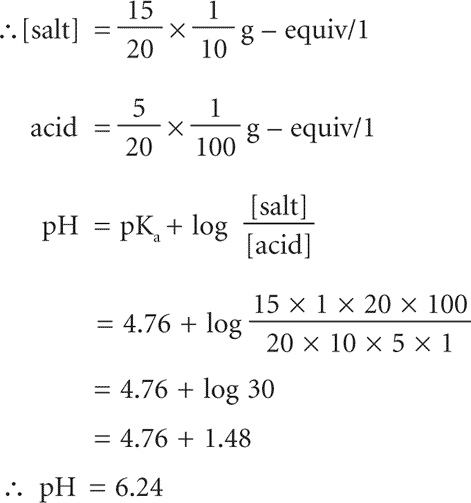
Determination of pH Values
The two most important methods of measuring pH are by the use of coloured indicators or of special electrodes.
Colorimetric Method for Determining pH
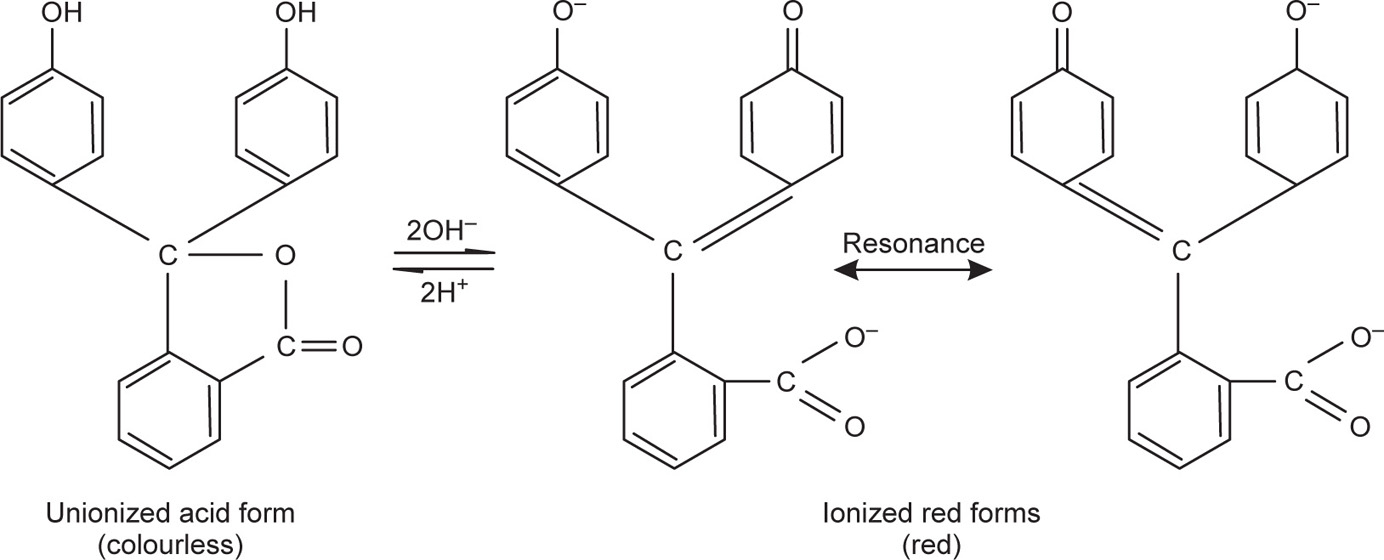
Indicators are either weak acids or bases, which exist in two tautomeric forms. These two forms differ in colour and distribution of their valency electrons, e.g. phenolphthalein:
The colour of any indicator added to a test solution depends on the ratio of the ionized: unionized forms present and this, in turn, depends on the pH of the solution. Maximum sensitivity to pH change occurs when the concentrations of unionized and ionized forms are equal, i.e. when the pH equals the pKa of the indicator. The usable range of a single indicator varies by about± 1.5 pH units on either side of the pKa value of the indicator; for example, phenolphthalein has a pKa = 9.4 and a useful pH range of pH 8.2–10.0. Mixtures of indicators can be made, which can cover most of the range of the pH scale; these ‘universal’ indicators are available as liquids or test papers and are useful in determining pH to approximately± 1 unit.
To determine the pH correct to about ±0.2 units, a small sample of the test solution should be mixed with an equal volume of an indicator solution whose working range covers the pH of the test solution. Samples from buffer solutions made up in 0.2 pH intervals are treated in a similar manner and the pH of the test solution determined by direct colour comparisons. Sets of these buffer solutions already admixed with the indicator and in sealed capillary tubes, known as capillators, are available commercially so it is possible to measure pH values of test solutions within a minute or two. It is important that these standard colours are protected from light to prevent fading.
For larger volumes of test liquid, comparators are used. Essentially, these are test tubes used in a manner similar to capillators but are particularly useful when turbid or coloured solutions are being examined. Tubes of distilled water or test solutions only can be placed in front of the tubes being compared (Fig. 2.1) so that the same total depth of liquid is viewed in each case and compensation is made for turbidity or colour not due to the indicator.
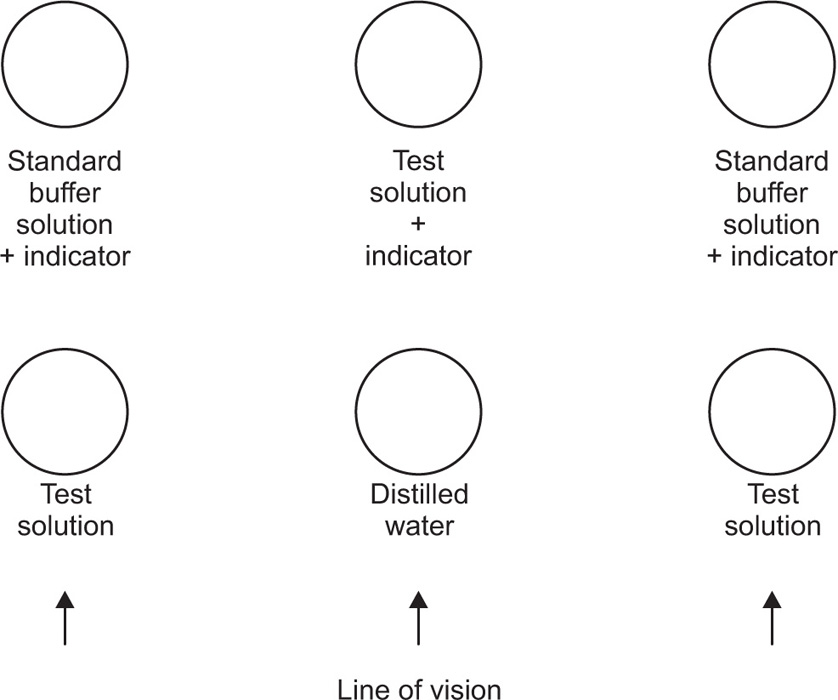
Fig. 2.1 Comparator (diagrammatic).
Electrometric Methods for Determining pH
Numerous indicator electrodes are available for the determination of pH and, without doubt, the glass electrode is the most widely used. The glass electrode consists of a thin glass bulb of special glass blown at the end of a glass tube and the bulb is filled with dilute acid, e.g. decinormal hydrochloric acid. A silver–silver chloride electrode (a silver wire electrolytically coated with silver chloride) makes the necessary electrical connection with the acid whose pH remains constant. Several types of glass are used to make the pH-sensitive glass bulb and those made of lithia glass are suitable over most of the range pH 0–14. When the glass bulb is immersed in a solution of unknown pH (pHx) a potential EH is set up across the glass according to the equation:
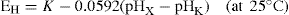
or, by combining constants:
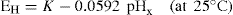
K is known as the asymmetry potential and varies from time to time although it is usually reasonably constant over the period of a working day unless the electrode is subjected to extremes of pH.
To measure the pH of a solution, the bulb of the glass electrode and a suitable reference electrode is immersed in a sample of the solution and the two electrodes connected to a pH meter. The reference electrode is essential for the second electrical contact with the solution and must, of course, have a constant potential irrespective of the pH of the solution (Fig. 2.2).
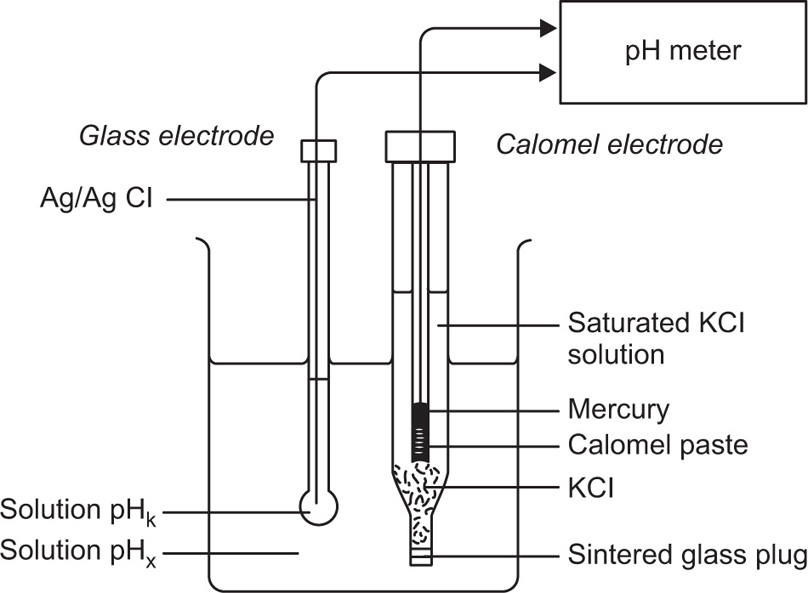
Fig. 2.2 Electrode system for pH measurement.
A simple potentiometer cannot be used to measure the potential difference between the two electrodes because the glass electrode has an exceptionally high resistance (>100MΩ). This means that any current flowing in the circuit would be insufficient to affect any ordinary galvanometer without some form of electronic amplification.
All pH meters are operated in essentially the same way. The electrical zero of the pH meter is adjusted, if necessary, and, with the electrodes immersed in a buffer solution of standard pH, the asymmetry potential control altered until the meter reads the known pH value of the buffer solution. These standardized electrodes, after rinsing with distilled water, are then immersed in the test solution and the pH value of the solution read from the meter either directly in the case of deflection meters, or after adjusting to a null balance in the case of potentiometric type meters.
Several standard pH solutions are available for the calibration of pH meters, the most popular being 0.05M potassium hydrogen phthalate solution. Table 2.2 shows the pH of this and some other solutions over a wide temperature range.
Table 2.2 pH of standard solutions at various temperatures
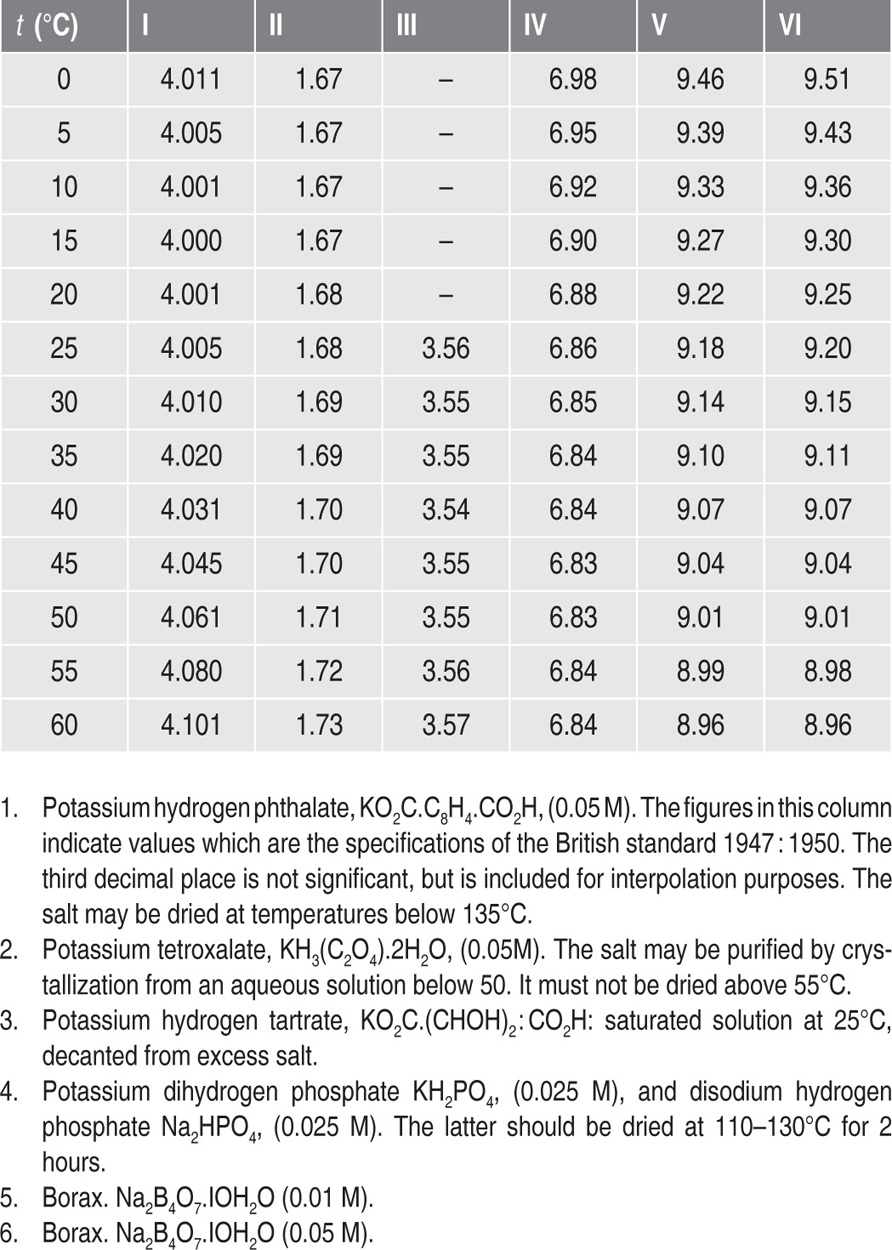
The following points should be noted:
1. Good distilled water (pH 6–7) should be used for acid buffer solutions. Freshly boiled and cooled distilled water (i.e. CO2 free) must be used for alkaline buffer solutions.
2. The pH values change slightly on dilution with water. The above solutions when diluted with an equal volume of water increase in pH value: I. +0.052; II. +0.186; III. +0.049; IV. +0.049; V. +0.01.
3. Standard buffer solutions may be stored for up to 2 months in well-closed hard glass or polythene bottles. It is advisable to discard solutions if mould or sediment is visible.
Significance of pH in Pharmacy
The pH of many pharmaceutical preparations must be controlled to ensure optimum stability or physiological activity of the medicament. During the course of manufacture, the pH of the product can be influenced in various ways and a knowledge of the more important factors is useful in the formulation of such products.
Glass is a very useful material for storage but it imparts alkalinity to products stored in glass containers. Special glasses are available and the containers used for pharmaceutical purposes have to comply with tests which limit the alkalinity to acceptable proportions. Solutions that come into contact with filter materials of cotton and paper, for example, tend to make the solutions more alkaline. Distilled water, on the other hand, is usually acid (pH 4.5–6) due largely to dissolved carbon dioxide. Even when the dissolved gases are boiled off, the pH can become alkaline, rather than neutral, due to the alkalinity of the glass container.
Precipitation can sometimes occur if the pH of a solution is changed significantly and use can be made of this fact in the preparation of pharmaceutical products. When solutions of the salts of insoluble acids are acidified, the corresponding insoluble acids are precipitated, e.g. sodium benzoate or salicylate will deposit benzoic or salicylic acids, respectively.
The purification of proteins is simplified by the knowledge that amphoteric compounds are least soluble at the isoelectric point, e.g. insulin precipitates from aqueous solutions at pH 5–6. These examples illustrate how solubility is influenced by the degree of ionization which is controlled by pH, as shown by the following relationship:
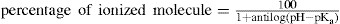
where pH refers to the pH of the solution and pKa to the weak acid or base under consideration.
The above formula is of particular interest when considering the biological activities of medicaments, since the unionized molecule and ionic species usually have difference activities. Unionized molecules penetrate cell membranes (which are lipid in character) more readily than ions and this accounts for the increased antimicrobial action of benzoic acid (pKa 4.2) and salicylic acid (pKa 2.97) in acidic solutions. On the other hand the antibacterial activity of the acridines depends on the amount of drug present as the cation, so for maximum effectiveness the pKa of these molecules should be numerically as near the pH of the body fluids (about pH 7.4) as possible to ensure that a large amount of the drug is in the ionized form.
Enzymes have maximal activity and stability at definite pH values and outside certain limits they are rendered inactive and may even be destroyed. Thus pepsin has maximal activity at pH 1.5, and is, therefore, effective in the gastric fluid but is rendered inactive in the duodenum where the pH is about 8.
Many compounds are unstable in aqueous solution because hydrolysis takes place. Often, however, the solutions can be stabilized by adjustment of the pH. Basic esters such as amethocaine, amylocaine and procaine require acid conditions to achieve stability. Vitamins are often stable only over a narrow pH range and many B.P. injections are adjusted to a definite pH to ensure stability of the product.
Redox Potentials
When an ion is oxidized it donates electrons to another ion which is simultaneously reduced by accepting the donated electrons. Thus ferrous iron loses an electron on oxidation to ferric iron:
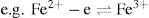, the converse is also true:
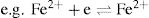, this can be expressed in more general terms, thus:
,
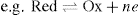where Red refers to the reduced state (reductant) and Ox refers to the oxidized state (oxidant) of the ion; ne is the number of electrons involved in the reaction.
Oxidation–reduction (redox) systems that are under equilibrium conditions can be studied in a similar manner to pH systems but by using an inert (e.g. platinum) indicator electrode together with a reference electrode (e.g. calomel electrode). A potential is set up under these conditions, which depends on the relative concentrations of oxidant and reductant. This potential (Eh) is given by the Nernst equation:
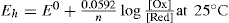
where n is the number of electrons transferred per ion and E0 is the standard oxidation–reduction potential. It will be observed that when the concentrations of oxidant and reductant are equal, then Eh = E0. The potential Eh can be determined by use of a potentiometer to measure the potential difference (Ecell) between the indicator electrode (whose potential is Eh) and the reference electrode (Eref) according to the following relationship:
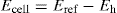
The E0 of a redox system is a characteristic constant and gives a measure of its oxidizing or reducing tendency. The higher the E0 value, the greater is the oxidizing ability of the system; the lower the E0 value, the greater is the reducing power of the system, i.e. a system of higher E0 value will oxidize a second system of lower E0. Where redox reactions occur, which involve the hydrogen ion, then its concentration must be considered. Thus in the reaction:
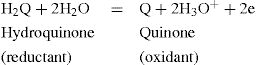
the potential at 25°C is:
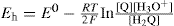
or, expressed more generally:
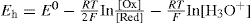
This equation shows that Eh is reduced if the hydrogen ion concentration (activity) is increased or the pH decreased. It is sometimes convenient in systems of a definite pH to combine the last term of the equation with the E0 to give a standard potential E0 characteristic of the system at a fixed pH. The standard potentials E0 for some redox systems of pharmaceutical interest are given in Table 2.3.
Table 2.3 Standard potentials of specified pH at 30°C |
||
| Redox system | E0 (V) | pH |
| Adrenalin | 0.380 | 7.0 |
| Ascorbic acid | 0.115 0.136 |
5.2 4.6 |
| 2,6-Dichlorphenolindophenol | 0.217 | 7.0 |
| Methylene blue | 0.011 | 7.0 |
| Riboflavin | –0.208 –0.117 |
7.0 5.0 |
As in the determination of pH, it is possible to use certain dyes to determine the value of Eh approximately as the colour of such dyes varies with their state of oxidation. Methylene blue, for example, changes from almost colourless to a deep blue (at pH 7) as Eh varies from 0.040 to –0.062 V. Redox indicators can also be used effectively to determine the equivalence point in redox titrations.
References
Andrasi M, Buglyo P, Zekany L, Gaspar A. J. Pharm. Biomed. Anal. 2007;44:1040.
Avdeef A. Absorption and Drug Development: Solubility, Permeability, and Charge State. New York: Wiley; 2003.
Beck MT, Nagypál I. Chemistry of Complex Equilibria. Horwood; 1990.
Beltran JL, Sanli N, Fonrodona G, Barron D, Ozkan G, Barbosa J. J. Anal. Chim. Acta. 2003;484:253.
Erdemgil FZ, Sanli S, Sanli N, Ozkan G, Barbosa J, Guiteras J, Beltran JL. Talanta. 2007;72:489.
Evagelou V, Tsantili-Kakoulidou A, Koupparis M. J. Pharm. Biomed. Anal. 2003;31:1119.
Eyal AM. Acid Extraction by Acid–Base-Coupled Extractants.. Ion Exchange and Solvent Extraction: A Series of Advances. 1997;13:31–94.
Good NE, Winget GD, Winter W, Connolly TN, Izawa S, Singh RMM. Hydrogen Ion Buffers for Biological Research.. Biochemistry. 1966;5(2):467–477.
Hilal SH, El-Shabrawy Y, Carreira LA, Karickhoff SW, Toubar SS, Rizk M. Talanta. 1996;43:607–619.
Jimenez-Lozano E, Marques I, Barron D, Beltran JL, Barbosa J. Anal. Chim. Acta. 2002;464:37.
Onufriev A, Case DA, Ullmann GM. A Novel View of pH Titration in Biomolecules.. Biochemistry. 2001;40(12):3413–3419.
Qiang Z, Adams C. Water Res. 2004;38:2874.
Sandra Babic, Alka JM, Horvat Dragana Mutavdzic Pavlovic, Kastelan-Macan Marija. Determination of pKa values of active pharmaceutical ingredients.. Trends Anal. Chem. 2007;26(11):1043–1061.
Szakacs Z, Hagele G. Talanta. 2004;62:819.
Van Leeuwen CJ, Hermens LM. Risk Assessment of Chemicals: An Introduction. Springer; 1995:254–255.