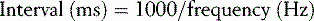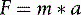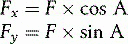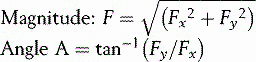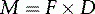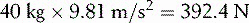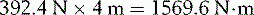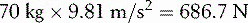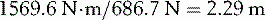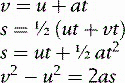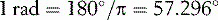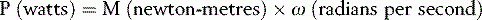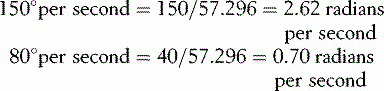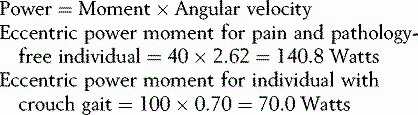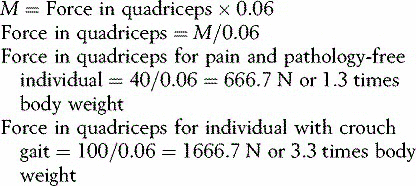1 Basic sciences
All voluntary movement, including walking, results from a complicated process involving the brain, spinal cord, peripheral nerves, muscles, bones and joints. Before considering in detail the process of walking, what can go wrong with it and how it can be studied, it is necessary to have a basic understanding of three scientific disciplines: anatomy, physiology and biomechanics. It is hoped that this chapter will provide the rudiments of these subjects for those not already familiar with them, review the topic for those who are, and also provide a convenient source of reference material.
Anatomy
It is not the intention of this book to teach in detail the anatomy of the locomotor system, which is well covered in several other books (e.g. Gray's Anatomy, 2009). The notes which follow give only an outline of the subject, but one which should be sufficient for an understanding of gait analysis. The anatomical names for the different parts of the body vary somewhat from one textbook to another, and as far as possible the most common name has been used. The section starts by describing some basic anatomical terms and then goes on to describe the bones, joints, muscles and nervous system. Although the arteries and veins are essential to the functioning of the locomotor system, they will not be described here since they generally affect gait only indirectly, through their role in providing oxygen and nutrients for the nerves and muscles and removing waste products.
Basic anatomical terms
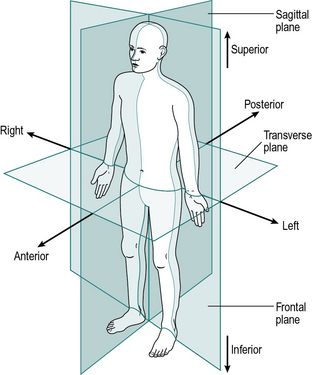
The anatomical terms describing the relationships between different parts of the body are based on the anatomical position, in which a person is standing upright, with the feet together and the arms by the sides of the body, with the palms forward. This position, together with the reference planes and the terms describing the relationships between different parts of the body, is illustrated in Figure 1.1.
Six terms are used to describe directions in relation to the centre of the body. These are best defined by example:
The anterior surface of the body is ventral and the posterior surface is dorsal. The word dorsum is used for both the back of the hand and the upper surface of the foot. The terms cephal (towards the head) and caudal (towards the ‘tail’) are sometimes used in place of superior and inferior.
Within a single part of the body, six additional terms are used to describe relationships:
1. Medial means towards the midline of the body: the big toe is on the medial side of the foot
2. Lateral means away from the midline of the body: the little toe is on the lateral side of the foot
3. Proximal means towards the rest of the body: the shoulder is the proximal part of the arm
4. Distal means away from the rest of the body: the fingers are the distal part of the arm
5. Superficial structures are close to the surface: the skin is superficial to the bones
6. Deep structures are far from the surface: the heart is deep to the sternum.
The motion of the limbs is described using reference planes:
1. A sagittal plane is any plane which divides the body into right and left portions; the median plane is the midline sagittal plane, which divides the whole body into right and left halves
2. A coronal (or frontal) plane divides a body part into front and back portions
3. A transverse (or horizontal) plane divides a body part into upper and lower portions.
The term coronal plane is equivalent to frontal plane and the transverse plane may also be called the horizontal plane, although it is only horizontal when in the standing position.
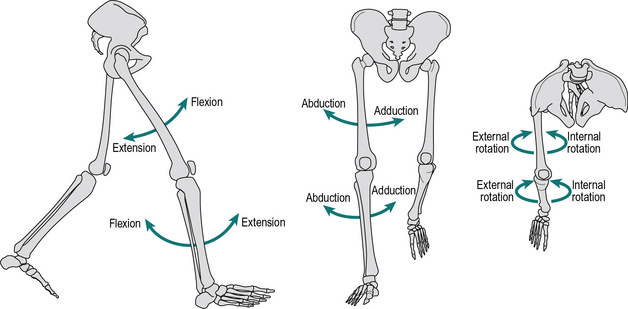
Most joints have their largest amount of movement in the sagittal plane, although the coronal and transverse planes can be very important clinically. The directions of these motions for the hip and knee are shown in Figure 1.2 and for the ankle and foot in Figure 1.3. The possible movements are as follows:
1. Flexion and extension take place in the sagittal plane; in the ankle these movements are called dorsiflexion and plantarflexion, where the foot (distal segment) moves up or down relative to the tibia (proximal segment), respectively
2. Abduction and adduction take place in the frontal plane, where the distal segment moves away or towards the midline of the body relative to the proximal segment, respectively
3. Internal and external rotation take place in the transverse plane; they are also called medial and lateral rotation, respectively, the term referring to the motion of the anterior surface of the distal segment relative to the proximal.
Other terms which are used to describe the motions of the joints or body segments are:
1. Varus (adducted) and valgus (abducted), which describe an angulation of a joint towards or away from the midline, respectively, when viewed in the coronal plane. Therefore knock knees are in valgus and bow legs are in varus.
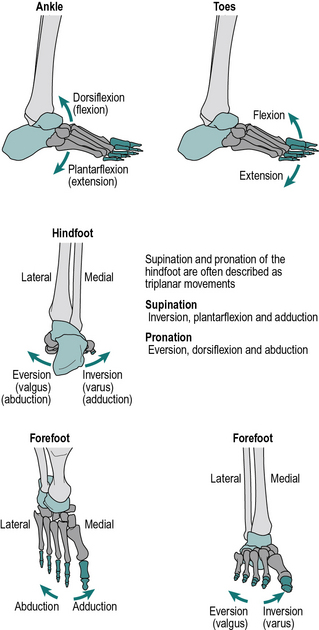
2. Pronation and supination, which are internal and external rotations of the hand about the long axis of the forearm. Pronation of both hands brings the thumbs together, supination brings the little fingers together (aide memoire: you can hold soup in your hands if the palms are upwards). Internal and external rotation of the foot about the long axis of the tibia has also been used to describe pronation and supination of the foot and ankle complex.
3. Inversion (adduction) of the feet brings the soles together; eversion (abduction) causes the soles to point away from the midline when viewed in the coronal plane.
Terminology in the foot is often confusing and lacking in standardisation. This book has adopted what is probably the commonest convention (Fig. 1.3), in which the term pronation is used for a combined movement which consists primarily of eversion but also includes some dorsiflexion and forefoot abduction. Similarly, supination is primarily inversion, but also includes some plantarflexion and forefoot adduction. These movements represent a ‘twisting’ of the forefoot (distal segment), relative to the hindfoot (proximal segment). However, some authorities regard pronation and supination as the basic movements and eversion and inversion as the combined movements. Increasingly the foot is being modelled in multiple segments, most commonly into three or four segments although more have been used. This requires further referencing of the relative movement of the different segments, which will be dealt with later in the chapter.
Bones
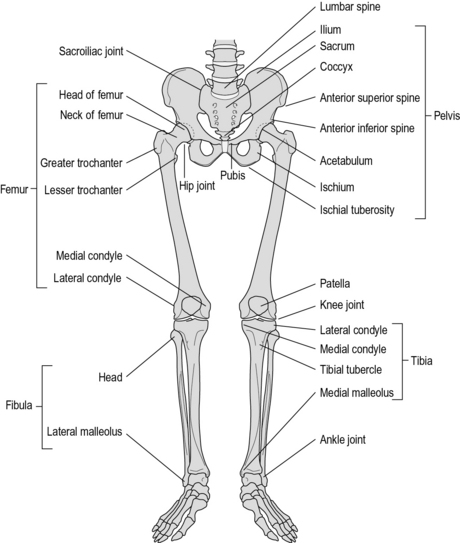
It could be argued that almost every bone in the body takes part in walking. However, from a practical point of view, it is generally only necessary to consider the bones of the pelvis and legs. These are shown in Figure 1.4.
The pelvis is formed from the sacrum, the coccyx and the two innominate bones. The sacrum consists of the five sacral vertebrae, fused together. The coccyx is the vestigial ‘tail’, made of three to five rudimentary vertebrae. The innominate bone on each side is formed by the fusion of three bones: the ilium, ischium and pubis. The only real movement between the bones of the pelvis occurs at the sacroiliac joint and this movement is generally very small in adults. It is thus reasonable, for the purposes of gait analysis, to regard the pelvis as being a single rigid structure. The superior surface of the sacrum articulates with the fifth lumbar vertebra of the spine. On each side of the lower part of the pelvis is the acetabulum, which is the proximal part of the hip joint, being the socket into which the head of the femur fits.
The femur is the longest bone in the body. The spherical femoral head articulates with the pelvic acetabulum to form the hip joint. The neck of the femur runs downwards and laterally from the femoral head to meet the shaft of the bone, which continues downwards to the knee joint. At the junction of the neck and the shaft are two bony protuberances, where a number of muscles are inserted – the greater trochanter laterally, which can be felt beneath the skin, and the lesser trochanter medially. The bone widens at its lower end to form the medial and lateral condyles. These form the proximal part of the knee joint and have a groove between them anteriorly, which articulates with the patella.
The patella or kneecap is a sesamoid bone; that is to say, it is embedded within a tendon, in this case the massive quadriceps tendon, which below the patella is known as the patellar tendon. The anterior surface of the patella is subcutaneous (immediately below the skin); its posterior surface articulates with the anterior surface of the lower end of the femur to form the patellofemoral joint. The patella has an important mechanical function, which is to displace the quadriceps tendon forwards, thereby improving its leverage.
The tibia extends from the knee joint to the ankle joint. Its upper end is broadened into medial and lateral condyles, with an almost flat upper surface which articulates with the femur. The tibial tubercle is a small bony prominence on the front of the tibia, where the patellar tendon is inserted. The anterior surface of the tibia is subcutaneous. The lower end of the tibia forms the upper and medial surfaces of the ankle joint, with a subcutaneous medial projection called the medial malleolus.
The fibula is next to the tibia on its lateral side. For most of its length it is a fairly slim bone, although it is broadened at both ends, the upper end being known as the head. The broadened lower end forms the lateral part of the ankle joint, with a subcutaneous lateral projection known as the lateral malleolus. The tibia and fibula are in contact with each other at their upper and lower ends, as the tibiofibular joints. Movements at these joints are very small and will not be considered further. A layer of fibrous tissue, known as the interosseous membrane, lies between the bones.
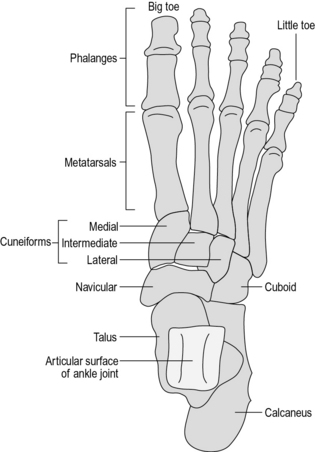
The foot is a very complicated structure (Fig. 1.5), which is best thought of as having four parts:
1. The hindfoot, which consists of two bones, one on top of the other
2. The midfoot, which consists of five bones, packed closely together
3. The forefoot, which consists of the five metatarsals
4. The toes, which consist of the five sets of phalangeal bones.
The talus or astragalus is the upper of the two bones in the hindfoot. Its superior surface forms the ankle joint, articulating above and medially with the tibia and laterally with the fibula. Below, the talus articulates with the calcaneus through the subtalar joint. It articulates anteriorly with the most medial and superior of the midfoot bones – the navicular.
The calcaneus or os calcis lies below the talus and articulates with it through the subtalar joint. Its lower surface transmits the body weight to the ground through a thick layer of fat, fibrous tissue and skin – the heelpad. The anterior surface articulates with the most lateral and inferior of the midfoot bones – the cuboid.
The midfoot consists of five bones:
1. The navicular, which is medial and superior
2. The cuboid, which is lateral and inferior
3. Three cuneiform bones (medial, intermediate and lateral), which lie in a row, distal to the navicular.
The five metatarsals lie roughly parallel to each other, the lateral two articulating with the cuboid and the medial three articulating with the three cuneiform bones.
The phalanges are the bones of the toes; there are two in the big toe and three in each of the other toes. The big toe is also called the great toe or hallux.
Joints and ligaments
A joint is the region where two bones come in contact with each other. From a practical point of view, they can be divided into synovial joints, in which significant movement can take place, and the various other types of joint in which only small movements can occur. Since gait analysis is usually only concerned with fairly large movements, the description which follows deals only with synovial joints. In a synovial joint, the bone ends are covered in cartilage and the joint is surrounded by a synovial capsule, which secretes the lubricant synovial fluid. Most joints are stabilised by ligaments, which are bands of relatively inelastic fibrous tissue connecting one bone to another. Fascia is a special type of connective tissue, being a continuous web of tissue found throughout the human body.
The hip joint is the only true ball-and-socket joint in the body, the ball being the head of the femur and the socket the acetabulum of the pelvis. Extremes of movement are prevented by a number of ligaments running between the pelvis and the femur, by a capsule surrounding the joint and by a small ligament – the ligamentum teres – which joins the centre of the head of the femur to the centre of the acetabulum. The joint is capable of flexion, extension, abduction, adduction, and internal and external rotation (Fig. 1.2).
The knee joint consists of the medial and lateral condyles of the femur, above, and the corresponding condyles of the tibia, below. The articular surfaces on the medial and lateral sides are separate, making the knee joint, in effect, two joints, side by side. The femoral condyles are curved both from front to back and from side to side, whereas the tibial condyles are almost flat. The ‘gap’ this would leave around the point of contact is filled, on each side, by a ‘meniscus’, commonly called a ‘cartilage’, which acts to spread the load and reduce the pressure at the point of contact.
The motion of the joint is controlled by five structures which, between them, exert very close control over the movements of the knee:
1. The medial collateral ligament (MCL), which prevents the medial side of the joint from opening up (i.e. it opposes abduction or valgus)
2. The lateral collateral ligament (LCL) similarly opposes adduction or varus
3. The posterior joint capsule, which prevents hyperextension (excessive extension) of the joint
4. The anterior cruciate ligament (ACL), in the centre of the joint, between the condyles; it is attached to the tibia anteriorly and the femur posteriorly. It prevents the tibia from moving forwards relative to the femur and also helps to prevent hyperextension of the knee as well as excessive internal rotation of the tibia
5. The posterior cruciate ligament (PCL), also in the centre of the joint, is attached to the tibia posteriorly and the femur anteriorly and prevents the tibia from moving backwards relative to the femur and also helps to limit external rotation of the tibia.
The anterior and posterior cruciate ligaments are named for the positions in which they are attached to the tibia. They appear to act together as what engineers call a ‘four-bar linkage’, which imposes a combination of sliding and rolling on the joint and moves the contact point forwards as the joint extends and backwards as it flexes. This means that the axis about which the joint flexes and extends is not fixed, but changes with the angle of flexion or extension. Pollo et al. (2003) challenged this description, saying that it only occurs in the unloaded knee and that during walking, the tibia moves backwards relative to the femur as the knee flexes.
In the normal individual, the motions of the knee are flexion and extension, with a small amount of internal and external rotation. Significant amounts of abduction and adduction are only seen in damaged knees. As the knee comes to full extension, there is an external rotation of a few degrees: the so-called automatic rotation or ‘screw-home’ mechanism.
The patellofemoral joint lies between the posterior surface of the patella and the anterior surface of the femur. The articular surface consists of a shallow V-shaped ridge on the patella, which fits into a shallow groove between the medial and lateral condyles. The principal movement is the patella gliding up and down in this groove, during extension and flexion of the knee, respectively. This causes different areas of the patella to come into contact with different parts of the joint surfaces of the femur. There is also some medial-lateral movement of the patella.
The ankle or talocrural joint has three surfaces: upper, medial and lateral. The upper surface is the main articulation of the joint; it is cylindrical and formed by the tibia above and the talus below. The medial joint surface is between the talus and the inner aspect of the medial malleolus of the tibia. Correspondingly, the lateral joint surface is between the talus and the inner surface of the lateral malleolus of the fibula.
The major ligaments of the ankle joint are those between the tibia and the fibula, preventing these two bones from moving apart, and the collateral ligaments on both sides, between the two malleoli and both the talus and calcaneus, which keep the joint surfaces in contact. The ankle joint, being cylindrical, has only one significant type of motion – dorsiflexion and plantarflexion – corresponding to flexion and extension in other joints.
The subtalar or talocalcaneal joint lies between the talus above and the calcaneus below. It has three articular surfaces: two anterior and medial and one posterior and lateral. Large numbers of ligaments join the two bones to each other and to all the adjacent bones. The axis of the joint is oblique, running primarily forwards but also upwards and medially. From a functional point of view, the importance of the subtalar joint is that it permits eversion/inversion (abduction and adduction or a valgus/varus motion) of the hindfoot. When performing gait analysis, it is usually impossible to distinguish between movement at the ankle joint and that taking place at the subtalar joint and it is reasonable to refer to motion taking place at the ‘ankle/subtalar complex’. This motion in normal individuals includes dorsiflexion/plantarflexion, hindfoot abduction/adduction, and internal/external rotation about the long axis of the tibia.
The mid tarsal joints lie between each of the tarsal bones and its immediate neighbours, making for a very complicated structure. The movement of most of these joints is very small, as there are ligaments crossing the joints and the joint surfaces are not shaped for large movements. As a result, the mid tarsal joints may be considered together to provide a flexible linkage between the hindfoot and the forefoot, which permits a small amount of movement in all directions.
The tarsometatarsal joints, between the cuboid and the cuneiforms proximally and the five metatarsals distally, are capable of only small gliding movements, because of the relatively flat joint surfaces and the ligaments binding the metatarsals to each other and to the tarsal bones. There are also joint surfaces between adjacent metatarsals, except for the medial one.
The metatarsophalangeal and interphalangeal joints consist of a convex proximal surface fitting into a shallow concave distal surface. The metatarsophalangeal joints permit abduction and adduction as well as flexion and extension; the interphalangeal joints are restricted by their ligaments to flexion and extension, the range of flexion being greater than that of extension. In walking, the most important movement in this region is extension at the metatarsophalangeal joints.
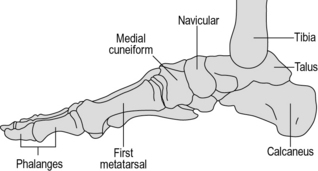
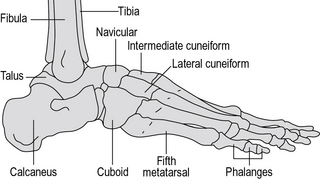
No description of the anatomy of the foot is complete without a mention of the arches. The bones of the foot are bound together by ligamentous structures, reinforced by muscle tendons, to make a flexible structure which acts like two strong curved springs, side by side. These are the longitudinal arches of the foot and they cause the body weight to be transmitted to the ground primarily through the calcaneus posteriorly and the metatarsal heads anteriorly. The midfoot transmits relatively little weight directly to the ground because it is lifted up, particularly on the medial side. The posterior end of both arches is the calcaneus. The medial arch (Fig. 1.6) goes upwards through the talus and then forwards and gradually down again through the navicular and cuneiforms to the medial three metatarsals, which form the distal end of the arch. The lateral arch (Fig. 1.7) passes forwards from the calcaneus through the cuboid to the lateral two metatarsals.
Muscles and tendons
Muscles are responsible for movements at joints. Most muscles are attached to different bones at their two ends and cross over either one joint (monarticular muscle), two joints (biarticular muscle) or several joints (polyarticular muscle). In many cases the attachment to one of the bones covers a broad area, whereas at the other end it narrows into a tendon, which is attached to the other bone. It is usual to talk about a muscle as having an ‘origin’ and an ‘insertion’, although these terms are not always clearly defined. Ligaments and tendons are obviously similar and frequently confused. As a general rule, ligaments connect two bones together, whereas tendons connect muscles to bones.
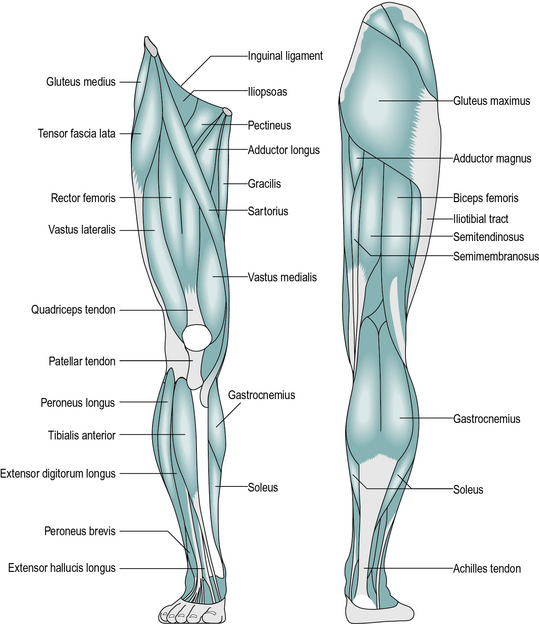
The following is a brief account of the muscles of the pelvis and lower limb, including their major actions. Most muscles also have secondary actions, which may vary according to the position of the joints, particularly with biarticular muscles. The larger and more superficial muscles are illustrated in Figure 1.8.
Muscles acting only at the hip joint
1. Psoas major originates from the front of the lumbar vertebrae. Iliacus originates on the inside of the pelvis. The two tendons combine to form the iliopsoas, inserted at the lesser trochanter of the femur; the main action of these two muscles is to flex the hip.
2. Gluteus maximus originates from the back of the pelvis and is inserted into the back of the shaft of the femur near its top; it extends the hip.
3. Gluteus medius and gluteus minimus originate from the side of the pelvis and are inserted into the greater trochanter of the femur; they primarily abduct the hip.
4. Adductor magnus, adductor brevis and adductor longus all originate from the ischium and pubis of the pelvis. They insert in a line down the medial side of the femur and adduct the hip.
5. Quadratus femoris, piriformis, obturator internus, obturator externus, gemellus superior and gemellus inferior originate in the pelvis and insert close to the top of the femur; they all externally rotate the femur, although most also have secondary actions.
6. Pectineus originates on the pubis of the pelvis; it runs laterally and inserts on the front of the femur, near the lesser trochanter; it flexes and adducts the hip.
Internal rotation of the femur was not mentioned in the above list; it is achieved as a secondary action by gluteus medius, gluteus minimus, psoas major, iliacus, pectineus and tensor fascia lata (described below).
Muscles acting across the hip and knee joints
1. Rectus femoris originates from around the anterior inferior iliac spine of the pelvis and inserts into the quadriceps tendon; it flexes the hip, as well as being part of the quadriceps, a group of four muscles which extend the knee.
2. Tensor fascia lata originates from the pelvis close to the anterior superior iliac spine and is inserted into the iliotibial tract, a broad band of fibrous tissue which runs down the outside of the thigh and attaches to the head of the fibula. The muscle abducts the hip and the knee.
3. Sartorius is a strap-like muscle originating at the anterior superior iliac spine of the pelvis and winding around the front of the thigh, to insert on the front of the tibia on its medial side; it is mainly a hip flexor.
4. Semimembranosus and semitendinosus are two of the hamstrings; both originate at the ischial tuberosity of the pelvis and are inserted into the medial condyle of the tibia; they extend the hip and flex the knee.
5. Biceps femoris is the third hamstring; it has two origins – the ‘long head’ comes from the ischial tuberosity and the ‘short head’ from the middle of the shaft of the femur. It inserts into the lateral condyle of the tibia and is a hip extensor and knee flexor.
6. Gracilis runs down the medial side of the thigh from the pubis to the back of the tibia on its medial side; it adducts the hip and flexes the knee.
Muscles acting only at the knee joint
1. Vastus medialis, vastus intermedius and vastus lateralis are three elements of the quadriceps muscle. They all originate from the upper part of the femur, on the medial, anterior and lateral sides, respectively. The fourth element of the quadriceps is rectus femoris, described above. The four muscles combine to become the quadriceps tendon. This surrounds the patella and continues beyond it as the patellar tendon, which inserts into the tibial tubercle. Quadriceps is the only muscle which extends the knee.
2. Popliteus is a small muscle behind the knee; it flexes and helps to unlock the knee by internally rotating the tibia at the beginning of flexion.
Muscles acting across the knee and ankle joints
1. Gastrocnemius originates from the back of the medial and lateral condyles of the femur; its tendon joins with that of the soleus (and sometimes also the plantaris) to form the Achilles tendon, which inserts into the back of the calcaneus. The main action of these muscles is to plantarflex the ankle, although the gastrocnemius is also a flexor of the knee.
2. Plantaris is a very slender muscle running deep to the gastrocnemius from the lateral condyle of the femur to the calcaneus; it is a feeble plantarflexor of the ankle.
Muscles acting across the ankle and subtalar joints
1. Soleus arises from the posterior surface of the tibia, fibula and the deep calf muscles. Its tendon joins with that of the gastrocnemius (and sometimes plantaris) to plantarflex the ankle. The soleus and gastrocnemius together are called the triceps surae.
2. Extensor hallucis longus, extensor digitorum longus, tibialis anterior and peroneus tertius form the anterior tibial group. They originate from the anterior aspect of the tibia and fibula and the interosseous membrane. The former two are inserted into the toes, which they extend; the latter two are inserted into the tarsal bones and raise the midfoot on the medial side (tibialis anterior) or lateral side (peroneus tertius). Tibialis anterior is the main ankle dorsiflexor; the others are weak dorsiflexors.
3. Flexor hallucis longus, flexor digitorum longus, tibialis posterior, peroneus longus and peroneus brevis are the deep calf muscles and all arise from the back of the tibia, fibula and interosseous membrane. The former two are flexors of the toes; the peronei are on the lateral side and evert the foot; tibialis posterior is on the medial side and inverts it. All five muscles are weak ankle plantarflexors.
Muscles within the foot
1. Extensor digitorum brevis and the dorsal interossei are on the dorsum of the foot; the former muscle extends the toes and the latter muscles abduct and flex the toes.
2. Flexor digitorum brevis, abductor hallucis and abductor digiti minimi form the superficial layer of the sole of the foot; they flex the toes and abduct the big toe and the little toe, respectively.
3. Flexor accessorius, flexor hallucis brevis and flexor digiti minimi brevis form an intermediate layer in the sole of the foot; between them they flex all the toes.
4. The adductor hallucis is in two parts – the oblique and transverse heads. It adducts the big toe.
5. The plantar interossei and the lumbricals lie in the deepest layer of the sole of the foot; the former adduct and flex the toes, the latter flex the proximal phalanges and extend the distal ones.
The above five groups of muscles are known together as the intrinsic muscles of the foot.
Spinal cord and spinal nerves
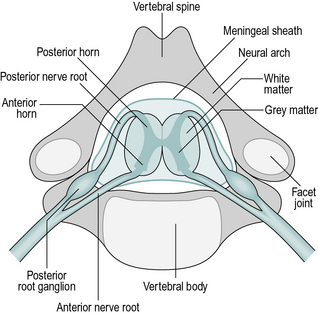
The spinal cord is an extension of the brain and plays an active role in the processing of nerve signals. Like the brain itself, it consists of white matter, which is bundles of nerve fibres, and grey matter, which contains many cell bodies and nerve endings, where the synapses (connections) between nerve cells take place. The spinal cord lies within the spinal canal, which is formed in front by the vertebral bodies and behind by the neural arches of the vertebrae (Fig. 1.9). The vertebrae are divided into four groups: cervical (7 vertebrae), thoracic (12), lumbar (5) and sacral (5). It is usual to use the abbreviated names, for example, the fourth thoracic vertebra is known as ‘T4’.
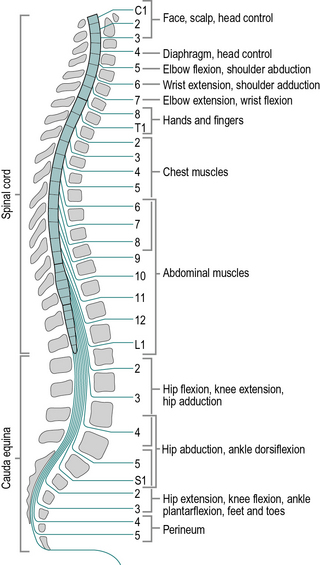
The spinal cord is shorter than the spinal canal, terminating in adults at approximately the level of the first lumbar vertebra (L1) and in children a little lower. Beyond the end of the spinal cord is a bundle of nerves known as the cauda equina, which consists of the nerve roots that enter and leave the lower levels of the spinal canal (Fig. 1.10). There are eight cervical nerve roots but only seven cervical vertebrae; each nerve root except the eighth emerges above the correspondingly numbered vertebra. In the remainder of the spine, the nerve roots emerge below the correspondingly numbered vertebrae.
The organisation of the neurons (nerve cells) of the spinal cord and the peripheral nerves is extremely complicated. It is possible to give here only a brief outline, although further details will be given in the physiology section later in this chapter. The main neurons responsible for muscle contraction pass down from the brain as upper motor neurons in the ‘descending’ tracts of the spinal cord. At the appropriate spinal level, they enter the grey matter and connect with the lower motor neurons, also called efferent neurons. The axons (nerve fibres) of these cells pass out of the spinal cord through the anterior root, combine with other spinal roots and then split into smaller and smaller nerves, finally reaching the muscle itself.
Nerve fibres also pass in the opposite direction, from the muscles, skin and other structures to the spinal cord. They enter the spinal cord at the posterior root, having passed through the posterior root ganglion, a swelling which contains the cell bodies of the neurons. These afferent neurons transmit many different types of sensory information. Some connect with the nerve fibres which pass up the spinal cord to the brain in the ‘ascending’ tracts, while others synapse with other nerve cells at the same or nearby spinal levels. Connections within the spinal cord are responsible for the spinal reflexes, which will be referred to later.
When the spinal cord is damaged by accident or disease, the results depend both on the spinal level at which the damage occurred and on whether the cord was totally or partially transected (cut through). A wide variety of disabilities may result from incomplete destruction of the spinal cord. If the cord is totally transected, the upper motor neurons are unable to control the muscle groups at or below that level, so voluntary control of those muscles is lost. There is also a total loss of sensation below the level of the damage. However, at levels below the damaged area, there is usually preservation of the lower motor neurons, the sensory nerves and the spinal reflexes. Injury to the vertebral column below L1 will damage the cauda equina, rather than the spinal cord. The cauda equina consists of lower motor neurons and sensory fibres and damage to it produces a totally different clinical picture from damage to the spinal cord itself.
Patients paralysed at the level of the cervical spine are tetraplegic or quadriplegic, with paralysis of the arms and legs. With a cervical lesion above C4, the diaphragm is also paralysed, making breathing difficult or impossible, and the chances of survival are poor. At the lower cervical levels, some arm or hand function is preserved. Where the spinal cord damage is at thoracic or lumbar level, only the legs are paralysed and the patient is paraplegic. Where only the cauda equina is damaged, the patient has an incomplete paraplegia and may be able to walk wearing some form of orthosis (an external support, also known as a brace or caliper). The word ‘orthotic’ was once synonymous with ‘orthosis’ but current usage restricts it to orthotic insoles, used within the shoes. Patients with paralysis restricted to one side of the body are hemiplegic. Sometimes the suffix ‘-paretic’ may be used in place of ‘-plegic’; it implies an incomplete paralysis.
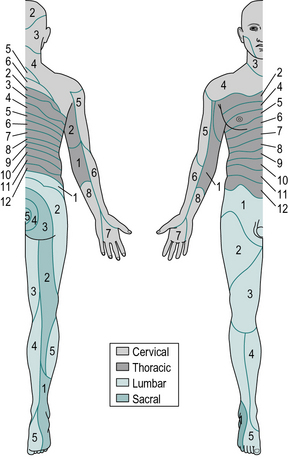
The area of skin served by the sensory nerves from a particular spinal root is known as a dermatome. The distribution of the dermatomes for all the spinal nerves is shown in Figure 1.11. In the legs, the anterior surface is innervated by the higher spinal segments and the posterior surface by the lower ones; loss of sensation from the buttocks and perineum is likely to follow spinal injury at almost any level.
Peripheral nerves
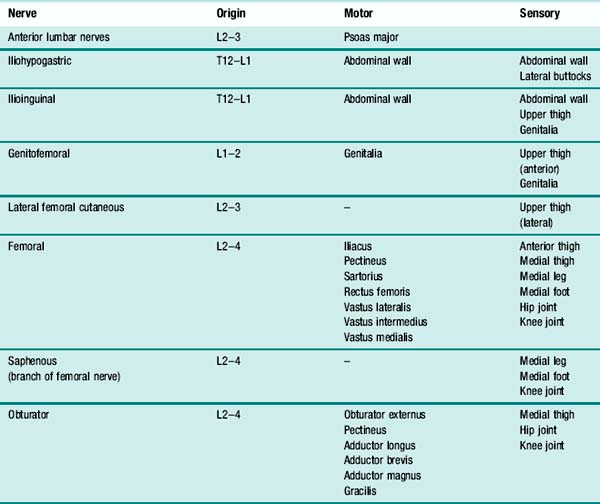
On emerging from the spinal cord, the spinal roots from adjacent levels form a network known as a plexus. The peripheral nerves which emerge from such a plexus usually contain nerve fibres from several adjacent spinal roots. The peripheral nerves supplying the muscles of walking all arise from either the lumbar plexus or the sacral plexus. Table 1.1 gives brief details of the motor and sensory distribution of the nerves arising from the lumbar plexus and Table 1.2 the corresponding information for the nerves arising from the sacral plexus (sometimes called the lumbosacral plexus).
Physiology
Again, the following text is only intended to give an overview of the most important aspects of physiology which apply to gait. There are many good textbooks on the subject; the authors use Guyton (2005).
Nerves
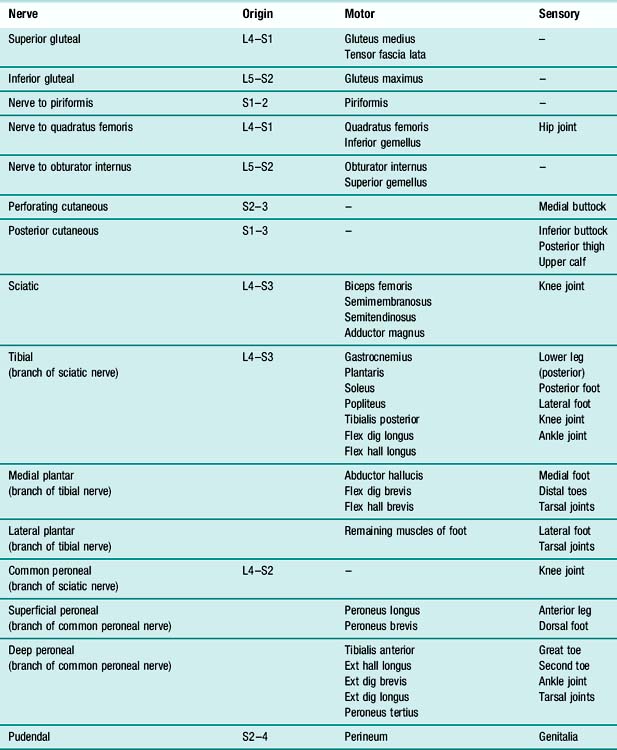
Mention has already been made of the nerve cell or neuron, the basic element of the nervous system. Although neurons in different parts of the nervous system vary considerably in structure, they all consist of four basic elements (Fig. 1.12): dendrites, cell body, axon and presynaptic endings. Nerve impulses are conducted from the dendrites to the cell body and thence down the axon to the presynaptic endings. These contain very small packages of a chemical known as a neurotransmitter, which is released and crosses a small space known as a synapse, to stimulate the dendrite of another neuron. Within the brain and spinal cord, dendrites are stimulated to produce nerve impulses by the axons of other cells and in turn the nerve impulse sent along the axon stimulates the dendrites of other neurons. The peripheral nerves contain motor neurons, whose axons stimulate muscle fibres, and sensory neurons, in which the dendrites are stimulated by the sense organs.
The brain and spinal cord consist of millions of neurons, connected together in a vast and complex network. A single peripheral nerve consists of the axons and dendrites of hundreds or even thousands of individual neurons. The tissues of the brain, spinal cord and peripheral nerves also contain a number of other types of cell known as neuroglia, whose functions are either to provide physical support for the neurons or to perform a variety of maintenance functions.
The upper motor neurons arise in several different areas of the brain, but most notably in an area known as the motor cortex, and pass down the spinal cord to the appropriate level, crossing over to the other side at some point in their journey. Within the anterior horn of grey matter, the upper motor neurons synapse with the lower motor neurons, as well as with a large number of other neurons, which take part in the complex system of motor control.
The motor or efferent neurons arise in the anterior horns of the spinal cord, emerge from the anterior spinal roots and pass down the peripheral nerves to the muscles. The axon usually branches at its distal end, where it synapses with the muscle cells at a number of motor endplates. The nerve impulse causes contraction of the muscle, by a process which will be described later.
The sensory nerves arise in the sense organs of the skin, joints, muscles and other structures. The sense organ itself stimulates the end of the dendrite of the afferent neuron. The dendrite usually commences as a number of branches; these come together and run up the peripheral nerve to enter the posterior root of the spinal cord. The cell body is in the posterior root ganglion (Fig. 1.9) and the axon runs from this ganglion into the spinal cord itself, usually terminating in the posterior horn of grey matter, where it synapses with other neurons. As well as the familiar sensations of touch, temperature, pain and vibration, sensory nerves also carry proprioception signals, which are used for feedback in the control of the limbs. These signals include the positions of the joints and the tension in the muscles and ligaments.
The term nerve impulse has been used above without explanation and it is now time to rectify this deficiency. The nature of the nerve impulse is a little difficult to grasp, since it is a complicated electrochemical process.
There are different concentrations of ions between the inside of cells (of all types) and the surrounding extracellular fluid. (Ions are atoms or molecules that have gained or lost one or more electrons, making them electrically charged.) The outside layer of a cell is known as the cell membrane; it is largely impermeable to sodium ions and any ions that leak in are ‘pumped’ out again. The inside of the cell contains large negatively charged ions, such as proteins, which are unable to pass through the cell membrane. The high concentration of positively charged sodium ions outside the cell, and of negative ions inside it, causes an automatic compensation, which results in a high concentration of potassium ions on the inside of the cell and of chloride ions outside. The inside of the cell thus has higher concentrations of potassium and large negative ions, while the outside has more sodium and chloride. The result of these imbalances in ionic concentration is a voltage difference between the inside and outside of the cell, across the thickness of the cell membrane. This membrane potential can be measured if a suitably small electrode is inserted. The normal resting membrane potential for a neuron is around − 70 mV, the negative sign indicating that the inside of the cell is negative with respect to the outside.
All body cells exhibit a membrane potential but nerve and muscle cells differ from other cells in that they can manipulate it, by altering the permeability of the cell membrane to sodium and potassium ions. This is the mechanism by which both nerve impulses and muscular contraction are propagated. If the membrane potential is lowered by about 20 mV, the membrane suddenly becomes extremely permeable to sodium ions, which enter rapidly from the extracellular fluid. While these ions are entering, the membrane potential is reversed to about + 40 mV and it is said to be depolarised. The increase in permeability to sodium ions is short-lived and is followed by an increased permeability to potassium ions, which leave the cell, thus restoring the ionic balance and returning the membrane potential to − 70 mV. The actual number of ions crossing the cell membrane is small and the overall composition of the cell is not affected to any appreciable extent; it is only when the sodium ions have entered, but before the potassium ions have left, that the membrane potential is reversed. This change in membrane potential by around 110 mV, from − 70 mV to + 40 mV, is known as an action potential.
Under normal circumstances, an action potential in a neuron begins in the synapses, in response to the neurotransmitters released from the presynaptic endings of the axons of other neurons. Some of these are excitatory, which means that they reduce the membrane potential, and some are inhibitory, in that they increase it. This combination of excitatory and inhibitory influences permits the addition and subtraction of nerve impulses. If the net effect of the various excitatory and inhibitory influences causes the membrane potential to fall by around 20 mV, an action potential will occur in that region of the neuron. This action potential spreads from its origin, crossing the cell body and running down the axon to its termination.
The action potential is an ‘all-or-none’ phenomenon, its size and shape being independent of the intensity of the stimulus, provided it is above the threshold; there are no ‘larger’ or ‘smaller’ action potentials. However, the spacing of the action potentials may vary; a nerve can pass action potentials one after another, in quick succession, or only occasionally and separated by long intervals. Thus it is the frequency of the nerve impulses, not their size, which carries the information on how hard the muscle is to be contracted, for example, or on the temperature of the skin.
Figure 1.13 shows an action potential passing along an axon from left to right. At its leading edge, sodium ions enter the axon, producing a region with reversed polarity. At the trailing edge of the action potential, potassium ions leave the axon and the membrane potential is restored. The depolarised region has a membrane potential of + 40 mV, whereas the surrounding regions have a membrane potential of around − 70 mV. This is equivalent to a tiny battery producing 110 mV and an electric current flows between the depolarised region and the surrounding normal regions of cell membrane. The passage of this electric current causes a drop in the membrane potential sufficient to generate an action potential in the normally polarised region in front, enabling the action potential to spread along the nerve. The region immediately behind an action potential becomes refractory, meaning that it cannot be stimulated again for a few milliseconds, so the action potential only moves in one direction.
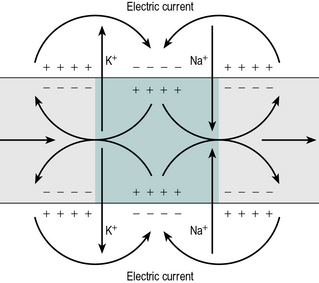
Fig. 1.13 • Propagation of an action potential along an axon. Electric current flows from positive regions (+) to negative regions (–). The depolarised region is coloured green.
The description so far has ignored the fact that many nerve fibres, particularly those required to send impulses quickly over long distances, are enclosed in a myelin sheath, as shown in Figure 1.12. Myelin is a fatty substance which surrounds nerve fibres, both axons and dendrites, as a series of sleeves, with gaps between them known as nodes of Ranvier. Since myelin is an insulator, it prevents the electric current from passing through the cell membrane close to an area of depolarisation, forcing it instead to pass through the next node of Ranvier, some distance along the nerve fibre. The effect of this is to cause the action potential to pass down the fibre in a series of jumps, known as saltatory conduction, which is much faster than the continuous propagation seen in unmyelinated fibres. A number of neurological diseases, most notably multiple sclerosis, are associated with loss of myelin from nerve fibres, with serious consequences to the functioning of the nervous system.
The speed at which nerve impulses travel depends on two things: the diameter of the nerve fibre and whether or not it is myelinated. Several types of fibres are found within the nervous system, known as types A, B and C. Type A fibres are all myelinated and are further divided by their conduction velocities into three groups:
Type B and C fibres are unmyelinated with conduction velocities around 10 m/s and 2 m/s, respectively. The type A fibres are the most important in gait analysis, especially the A-alpha fibres, which supply the motor nerves to muscles, and the A-beta and A-delta fibres, which conduct afferent impulses such as touch and/or pain. The gamma fibre is of particular importance in muscle physiology and will be referred to again later.
When an unmyelinated nerve fibre becomes damaged, recovery of function is usually impossible, because of the formation of scar tissue. For this reason, very little recovery of neuronal function takes place following damage to the brain or spinal cord, although function may be partially restored by the use of alternative neurological pathways. Myelinated fibres can recover, provided the cell body remains alive and the myelin sheaths remain in line; the nerve fibre regrows down the sheath at the rate of a few millimetres a week. In practice, if a complete nerve is divided and reconnected, most of the nerve fibres will enter the wrong myelin sheaths, although a sufficient number may be correctly connected to provide useful sensory and motor function.
Muscles
The human body contains three types of muscle: smooth, cardiac and skeletal. The description which follows is of skeletal muscle, also known as voluntary or striated muscle, which is responsible for the movement of the limbs.
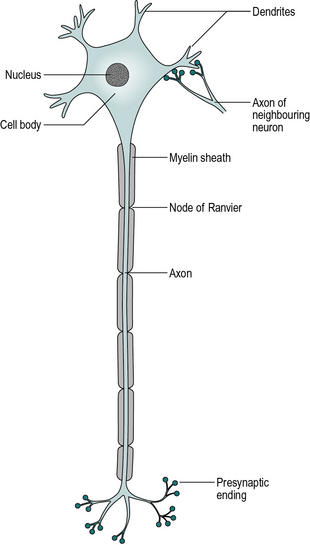
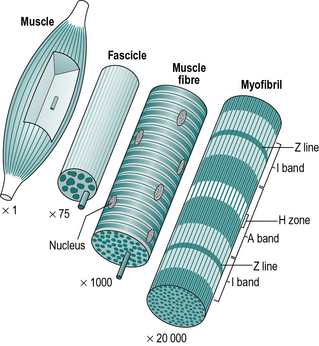
A muscle is made up of hundreds of fascicles (Fig. 1.14), which in turn consist of hundreds of muscle fibres. These large multinucleated cells (cells with many nuclei) are the basic units of muscle tissue. The fibre is itself made up of hundreds of myofibrils, which have a characteristic striated (striped) appearance. The striations are due to a regular arrangement of filaments, which are made of two types of protein – actin and myosin. It is the sliding of these filaments past each other, by the formation and destruction of cross-bridges, which is responsible for muscle contraction.
The various light and dark bands in the myofibril are identified by letters. The thin, dark ‘Z’ line is the origin of the slender actin filaments (Fig. 1.15). These are interleaved with the thicker myosin filaments, which form the ‘A’ band. The ‘I’ band and ‘H’ zone change their width during muscular contraction, as they represent the areas where the actin and myosin, respectively, are not overlapped – they were named before the process of contraction was understood!
There is an extremely complicated arrangement of membranes surrounding the myofibrils within the muscle fibre. It is responsible for the transport of nutrients and waste products and the transmission of the muscle action potential. Outside the muscle fibres are the blood capillaries and the terminal branches of the motor nerves, which connect to the muscle fibres at motor endplates, also known as neuromuscular junctions. On average, a single motor nerve will connect to about 150 muscle fibres, the combination of the neuron and the muscle fibres it innervates being known as a motor unit.
When an action potential passes down a nerve to the motor endplate, it results in the release of the transmitter substance acetylcholine (ACH). ACH diffuses across the synaptic cleft and binds to receptors on the muscle cell membrane causing depolarisation of the membrane, which causes a spreading wave of depolarisation. As this muscle action potential spreads throughout the muscle fibre, it causes the release of calcium ions, which trigger muscle contraction. Cross-bridges form between the actin and myosin molecules, pulling them together. The tension is maintained for a brief period, then released if no further action potential occurs, the calcium ions being removed by the calcium pump. The electrical activity of muscle action potentials can be detected and is known as the electromyogram (EMG).
The energy for muscular contraction comes from the release of a high-energy phosphate group from a chemical known as adenosine triphosphate (ATP). The regeneration of ATP requires the expenditure of metabolic energy and a failure to keep up with the demand results in muscle fatigue. There are two metabolic pathways involved in regeneration of ATP. One uses up chemicals stored within the cell (phosphocreatine and glucose), without the need for oxygen, and is known as anaerobic; the other requires oxygen and nutrients to enter the muscle fibre from the bloodstream and is known as aerobic. Anaerobic processes are quickly exhausted, although they can provide brief bursts of powerful contraction. For more sustained muscular effort, aerobic metabolism is required. Following anaerobic respiration, a muscle will have an oxygen debt, which will need to be ‘repaid’ by aerobic respiration, to remove lactic acid, which accumulates in the muscle.
If a single nerve impulse stimulates a muscle, it will respond, after a short pause known as the latent period, with a brief contraction known as a twitch (Fig. 1.16). If the motor nerve delivers a second nerve impulse during the latent period, it has no effect. The force which a muscle is able to generate in a contraction depends on a number of factors, particularly the strength of stimulation, the cross-sectional area of the muscle, the speed of contraction and the direction of contraction. The greatest force is usually produced when the muscle length is close to its middle range of length. If a muscle shortens to its minimum length, its force of contraction falls greatly (‘active insufficiency’). If the muscle becomes stretched over two or more joints it may be unable to stretch enough to complete full range of motion in both joints simultaneously. This is termed ‘passive insufficiency’. An example of this is that when the wrist is fully flexed with the fingers extended it becomes impossible to then fully flex the fingers as the finger extensor tendons have been stretched over several joints and cannot elongate further.
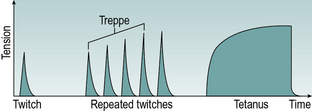
Fig. 1.16 • Response of a single muscle fibre to single stimulation and to repeated stimulation at low and high frequencies.
There are a number of different types of muscle fibre, the main subdivision being into types I and II. The type of muscle fibre depends on the nerve innervating it. Because of this, all the fibres in a single motor unit are of the same type. Type I fibres (slow twitch) are dark in colour, they contract and relax slowly and are fatigue resistant; they are used primarily for the sustained contractions used for posture control. Type II fibres (fast twitch) are pale in colour, quick to contract and relax, and easily fatigued. They are mainly used for brief bursts of powerful contraction. Depending on their function in the body, different muscles have different proportions of fast and slow fibres. This is also seen in poultry, where the ‘red meat’ in the leg muscles is used for sustained contraction and the ‘white meat’ in the wing muscles is used for bursts of powerful contraction. A change in the stimulation pattern will cause a change in the fibre type in the course of a few weeks, despite the fact that the fibre types differ in the actual structure of the myosin. This ability to alter the fibre type becomes very important when electrical stimulation is used on paralysed muscles.
When a muscle contracts, not all the motor units are active at the same time. If a stronger contraction is needed, further motor units are brought into use, a process known as recruitment.
If a muscle generates tension without changing its length, the contraction is known as isometric. If the muscle changes its length but the force of contraction remains the same, the contraction is isotonic. One normally thinks of a muscle shortening as it contracts – a concentric contraction. However, it is quite usual, particularly in gait, for a muscle to produce tension while it is lengthening – an eccentric contraction. For example, the quadriceps undergoes an eccentric contraction as you sit down. The muscle which is responsible for a particular action is known as an agonist. If two or more muscles act together, they are known as synergists; muscles which oppose agonists are known as antagonists. As a general rule, contraction of one set of muscles results in reciprocal inhibition of opposing muscles.
Muscle atrophy is the term used to describe the loss of bulk and strength of a muscle when it is not used. If the motor nerve is intact, the muscle fibres will become smaller but their numbers remain the same and subsequent restoration of muscle stimulation will lead to a full recovery of function. This happens, for example, when a limb is encased in plaster following a fracture. This type of muscle atrophy also occurs in spinal cord injury where the upper motor neurons are destroyed but the lower motor neurons remain intact. In contrast, if the lower motor neuron is destroyed, the muscle fibres shrink and become replaced by fibrous tissue. This leads to an irreversible form of muscle atrophy, such as is seen following poliomyelitis and after damage to the cauda equina or peripheral nerves.
Spinal reflexes
The lower motor neurons receive nerve impulses from both the brain and other neurons within the spinal cord. The two areas of the brain chiefly concerned with posture and movement are the motor cortex, which is responsible for voluntary movement, and the cerebellum, which is responsible for generating patterns of muscular activity. The motor cortex and its associated nerves are known as the pyramidal system; the cerebellum and some associated brain centres, with their associated nervous pathways, are known as the extrapyramidal system. Within the spinal cord itself, the influences of other neurons give rise to the spinal reflexes. There are also pattern generators for each limb within the spinal cord, which are capable of producing alternating flexion and extension.
The brain and higher centres exert an inhibitory influence on spinal reflexes, which as a result are often very weak in normal individuals. However, the reflexes may become very strong, due to the loss of this inhibition, in patients who have suffered damage to the brain or spinal cord.
One of the most important spinal reflexes (for the spinal nerve L4) is the stretch reflex, which is responsible for the knee-jerk, when the patellar tendon is struck by a small hammer. When a muscle is stretched, stretch receptors within it are stimulated, sending nerve impulses to the spinal cord along fast sensory neurons. Within the cord, these neurons synapse with and stimulate the lower motor neurons of the same muscle, causing it to contract. The stretch receptors are within the muscle spindles and attached to very small intrafusal muscle fibres, which are innervated by thin, relatively slow gamma motor neurons. These adjust the length of the spindle as the main muscle contracts and relaxes, so that it continues to work over the complete range of muscle lengths. The intrafusal fibres are also able to alter the ‘sensitivity’ of the stretch receptor. The stretch reflex provides a feedback system for maintaining the position of a muscle despite changes in the force applied to it. The stretch reflex is unusual in that it involves only a single synapse, between the sensory and motor neurons, making it a monosynaptic reflex. Most reflexes are polysynaptic, involving many intermediate neurons and often involving neurons on both sides of the spinal cord and at more than one spinal level.
Partly because of the stretch reflex and partly through a continuous low level of activity in the motor neurons, most muscles show a certain amount of resistance to being stretched – this is known as muscle tone. In some individuals this effect is exaggerated, giving the clinical condition of spasticity, in which muscle tone is very high, small movements of the limb being opposed by strong muscular contractions. Spasticity is an important cause of gait abnormalities. It usually results from the loss of some or all of the inhibitory influence of the higher centres on the spinal reflexes and is often seen in patients with brain damage (as in cerebral palsy) or following damage to the spinal cord. A related phenomenon, also seen in gait, is clonus in which a muscle produces a series of contractions, one after the other, in response to being stretched.
Many different types of sensory organ in the tissues are responsible for spinal reflexes, those of particular importance in gait analysis being the muscle spindle, referred to above, and the Golgi organ. The latter is a stretch receptor in tendons which inhibits muscular contraction if the force applied to the tendon, either actively or passively, becomes dangerously large. Pain receptors in the limb may elicit the flexor withdrawal reflex, in which the flexor muscles contract and the extensors relax, hopefully to remove the limb from whatever is causing the pain. There is also a crossed extensor reflex, where contraction of flexors on one side is accompanied by contraction of extensors on the other. An example of this is a person who has stepped on a nail with their right foot; the right leg flexes to move away from the pain and the left leg extends to hold the full body weight up.
Motor control
Walking is accomplished through a complex and coordinated pattern of nerve signals, sent to the muscles, which in turn move the joints, the limbs and the remainder of the body. The ‘central pattern generator’, which produces this pattern of nerve impulses, is not located in a single place but consists of networks of neurons in various parts of the brain and spinal cord. Much of the research in this area has been done on experimental animals but there is some evidence that human locomotion is organised in a similar fashion to that in cats, where a rhythm-generating system within the spinal cord is controlled by neural input from ‘higher levels’ in the brain and receives feedback from sensors in the muscles, joints and skin of the legs (Duysens and Van de Crommert, 1998).
Biomechanics
Biomechanics is a scientific discipline which studies biological systems, such as the human body, by the methods of mechanical engineering. Since gait is a mechanical process which is performed by a biological system, it is appropriate to study it in this way. Mechanical engineering is a vast subject but the descriptions which follow are limited to those aspects which are most relevant to gait analysis, especially time, mass, force, centre of gravity, moments of force, and motion, both linear and angular. The science of biomechanics can be extremely mathematical, but the basic principles are easy to grasp and the section ends with a worked example to illustrate this. A good text on the scientific basis of movement is Richards (2008).
Time
The second (s) and the millisecond (ms) are the primary units for time measurement in biomechanics, although it is still fairly common to find walking speed quoted in metres per minute or even miles per hour. When repeated events occur at short intervals of time, it is usual to quote a ‘frequency’ in hertz (abbreviated ‘Hz’), 1 Hz being one cycle per second. For example, a typical gait analysis system might measure the positions of markers on a patient's limbs at 100 Hz (corresponding to an interval between samples of 10 ms), the ground reaction force at 500 Hz (2 ms interval between samples) and EMG at 2000 Hz (0.5 ms interval between samples). The relationship between sample interval and frequency is given by:
Mass
As we all live in the Earth's gravitational field, we normally use the terms mass and weight to mean the same thing. However, there is a clear distinction between them. The mass of an object is the amount of matter contained in it, which does not depend on whether any gravity is present, whereas weight is the force exerted by gravity on the object. For example, in an orbiting spacecraft there is no gravity and all objects are weightless, although they still have mass. This means that you are still likely to be injured if someone throws a moon-rock at you inside a spacecraft, even though it doesn't ‘weigh’ anything! We casually talk about measuring our body ‘weight’ in kilograms (kg) or pounds but this is incorrect in scientific terms, as these are units of mass, not of force. As an example, a man with a mass of 90 kg (198 lb) has a weight of 882.9 N (90 kg * 9.81 m/s2).
Force
We are all familiar in general terms with the concept of force but the scientist uses the term in a particular way. Force is a vector quantity, which means that it has both magnitude and direction, in contrast to scalar quantities, such as temperature, which have only magnitude. The internationally agreed system for scientific measurement is the Système International (SI). The unit of force in this system is the newton (N). The force applied by normal earth gravity to a mass of 1 kg is 9.81 N; 1 N is the force exerted by gravity on a mass of about 102 g or 3½ ounces. This is easily visualised as being the weight of an average size apple! The earlier imperial and metric units of force were confusing and are best avoided; for conversions, see Appendix 2). The direction of a force vector may be stated in any convenient manner, for example 20 N downwards or 140 N at 30° to the x-axis. However, the direction should never be omitted, unless it is obvious.
The whole science of mechanical engineering is based on the three laws of force propounded by Sir Isaac Newton, which may be paraphrased as follows.
Newton's first law
A body will continue in a state of rest, or of uniform motion in a straight line, unless it is acted upon by an external force.
Newton's second law
An external force will cause a body to accelerate in the direction of the force. The acceleration (a) is equal to the size of the force (F) divided by the mass (m) of the object, as in the equation:
Newton's third law
To every action there is a reaction, which is equal in magnitude and opposite in direction.
Neglecting the strange behaviour of atomic and subatomic particles, all physical systems simultaneously obey all three of Newton's laws.
It is easy to remember which law is which if you first imagine a brick, just floating in space (first law); then someone pushes it and it accelerates (second law); as it is accelerating, the brick pushes back on whoever or whatever is pushing it (third law).
It is easy to see that a single force acting in one direction can be balanced out by an equal force acting in the opposite direction. A much more common situation, however, is to have a number of forces acting in different directions which, taken together, balance out each other. Provided that direction is taken into account, it is possible to add and subtract force vectors, as it is with any other vectors such as velocity or acceleration. To understand how this is possible, it is necessary to appreciate the fact that a single force, acting in a single direction, can be exactly equivalent to a number of different forces acting in other directions. Conversely, any number of separate forces can be represented by an appropriate single force.
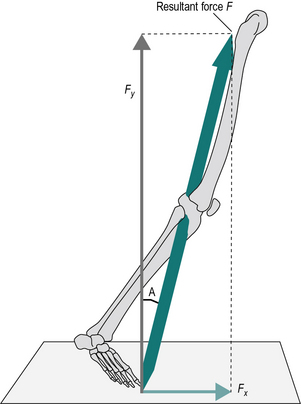
The technique used to convert a single force into two forces, acting in different directions, is known as resolving into components. Figure 1.17 shows how the resultant force F can be represented by two smaller forces, Fx and Fy, acting at right angles to each other. The magnitude of these forces is given by the formulae:
where A is the angle between the resultant force F and Fx.
The converse process (i.e. the combination of Fx and Fy to yield the resultant F), can be performed using these formulae:
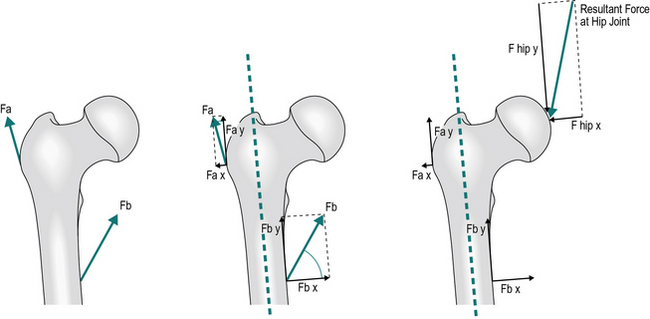
In order to combine forces, they are first resolved into components, using a common system of directions. Next, all the x components are added together and so are all the y components. The resulting totals are then used to find the single equivalent force. This is illustrated in Figure 1.18, where two forces, Fa and Fb represent resultant muscle forces acting around the hip joint. First, Fa and Fb are resolved into components (Fa x, Fa y, Fb x and Fb y). The algebraic sum of the x components gives the x component of the resultant force acting on the hip joint and similarly with the y components. Since Fa x and Fb x are in opposite directions, their algebraic sum is actually their difference. The resultant, R, is then obtained by recombining the x and y components.
It follows from Newton's second law that if an object is not accelerating, there can be no net force acting on it. Any forces which are acting on the object must be balanced out by other, equal and opposite forces. If the forces do not appear to balance, yet the object is not accelerating or decelerating, there must be at least one force which has not been taken into account.
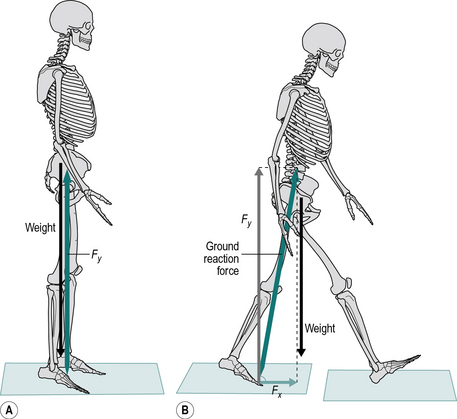
Figure 1.19A shows an individual standing perfectly still. In this case the ground reaction force will be equal and opposite to the weight of the person and will be acting only in a vertical direction with no horizontal component. However if we consider the forces during walking, in late stance phase there is a horizontal force Fx which is unopposed which will cause an acceleration or propulsion of the body forwards (Fig. 1.19B). We can also see that the vertical force Fy is greater than the weight of the person causing an acceleration of the body upwards.
Centre of gravity
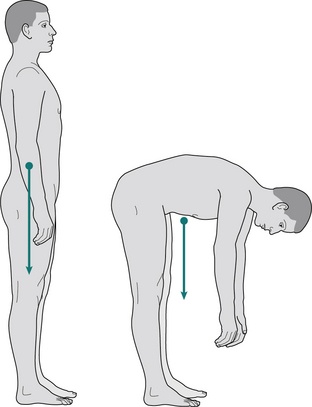
Although the mass of any object is distributed throughout every part of it, it is frequently convenient, as far as the effects of an applied force are concerned, to imagine that the whole mass is concentrated at a single point. This point, which should be called the centre of mass is usually called the centre of gravity. For a regular shape, such as a cube, made of a uniform material, it is easy to see that the centre of gravity must be at the geometric centre. However, for irregular and changing shapes, such as the human body, it may be necessary to determine it by direct measurement. It is also possible to determine the centre of gravity of every part of the body separately and to find the centre of gravity of the whole body by adding these together (by a method which is beyond the scope of this book). It is frequently stated that the centre of gravity of the body is just in front of the lumbosacral junction. This is approximately true for a person standing in the anatomical position but any movement of the body will move the centre of gravity. It is not even necessary for the centre of gravity to remain within the body; the centre of gravity of someone bending down to touch their toes will usually be outside the body, in front of the top of the thigh (Fig. 1.20). An interesting example of this is the technique used by skilled high-jumpers, who curve the body in such a way that although each part of the body in turn passes over the bar, the centre of gravity actually passes under it!
Moment of force
If an adult wishes to play with a small child on a seesaw, they will have to sit much closer to the pivot in order to balance the weight of the child (Fig. 1.21). The action which tends to unbalance the seesaw is the moment of force, which is calculated by multiplying the magnitude of the force by its perpendicular distance from the fulcrum or pivot point, this distance commonly being referred to as the lever arm or moment arm. The ‘moment of force’ may also be referred to as the ‘torque’, the ‘turning moment’ or simply the ‘moment’. The formula for calculating the moment of force is:
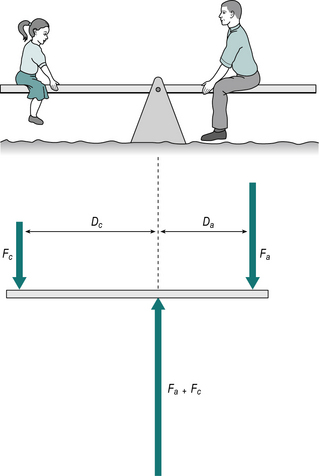
Fig. 1.21 • The adult on the seesaw will balance the child if the force Fa multiplied by the distance Da equals the force Fc multiplied by the distance Dc.
where M is the moment of force (in newton-metres, Nċm), F is the force (in newtons, N) and D is the distance (in metres, m).
For the system to be in equilibrium (that is, for the seesaw to balance), the sum of the clockwise moments of force must equal the sum of the anticlockwise moments. In Figure 1.21, if the child has a mass of 40 kg, she will exert a force due to gravity (Fc) of:
If her distance (Dc) from the fulcrum is 4 m, she exerts an anticlockwise moment of:
A 70 kg adult will produce a downward force (Fa) of:
This will produce an opposing clockwise moment of 1569.6 Nċm if he sits at a distance (Da) from the fulcrum of:
The definition of a moment of force refers to the perpendicular distance from the fulcrum. This is very important if opposing moments are produced by forces which act in different directions. Figure 1.22 illustrates the moments of force about the knee joint when standing with the knee bent. The ground reaction force is acting at a perpendicular distance ‘a’ from the point of loadbearing. The quadriceps tendon is pulling at an oblique angle relative to the vertical and the moment of force it provides is the product of the tension in the tendon and the perpendicular distance ‘b’. It will be noted that the presence of the patella increases the value of b and hence reduces the muscle force needed to produce a given moment of force. For equilibrium, the two moments (F1 × a) and (F2 × b) must be equal.
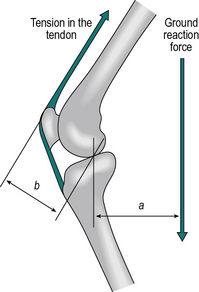
Fig. 1.22 • The moment of force due to ground reaction force, F1 multiplied by a, is opposed by contraction of the quadriceps, producing a moment of force F2 multiplied by b.
The measurement and interpretation of moments of force are essential for the full understanding of normal and pathological gait. ‘Active’ internal moments are generated by muscular contraction (concentric, isometric or eccentric). ‘Passive’ internal moments are generated by bone-on-bone forces and by tension in the soft tissues, especially ligaments. Moments may also be transmitted from adjacent joints. External moments (sometimes referred to as ‘reaction moments’) are generally due to gravitational forces. Modern gait analysis systems are able to measure the ‘net moment’ at the major joints during walking, which is the sum of all the active and passive moments present. However, this is seldom used to calculate the contraction force of a particular muscle, because there is frequently more than one muscle contracting. An example of this is ‘co-contraction’ at the hip joint, where flexor and extensor muscles contract at the same time, to increase the stability of the joint (Park et al., 1999).
Unfortunately, some confusion exists in the literature, because a term such as ‘flexor moment’ is often used without stipulating whether it refers to an internal or external moment. Contraction of a flexor muscle generates an internal flexor moment. In contrast, an external flexor moment attempts to flex the joint and is likely to be resisted by the contraction of extensor muscles (an example would be landing from a jump and the knee flexing from the force; the knee extensors would resist this external moment and prevent excessive knee flexion). To avoid such confusion, it is essential to make it clear whether any moment is internal or external. The gait analysis community now tends to use internal moments, a convention which has been adopted in this book, although the important textbook by Perry (1992) used external moments.
A couple is a moment that is produced by two equal forces which are parallel to each other but acting in opposite directions. The forces cancel each other out as far as producing linear motion is concerned (displacement or acceleration) but work together to produce rotation about a point between them.
In the same way that Newton's third law states that every force is opposed by another ‘equal and opposite’ force, every moment of force is opposed by an equal and opposite moment. It is impossible to generate a moment unless there is something to ‘push back’ with an opposing moment. The consequence of this for gait analysis is that if an external force generates a moment at a particular joint (attempting to flex the knee, for example), there must be a corresponding internal moment, generated within the joint, to oppose it. In the case of the knee, only the quadriceps muscles can provide an internal extensor moment, although for most joints both muscles and stretched ligaments can generate internal moments.
Any object which is supported by the ground will remain stable so long as the line of gravity (the line of force passing vertically downwards from the centre of gravity) remains within the area on the ground which is supporting it. Should the line of gravity stray outside this area, one of two things can happen: it may automatically correct itself, as happens with a self-righting lifeboat, or it may fall over, as will happen with a pencil balanced on its point. The former is a stable equilibrium, where a degree of imbalance produces ‘restoring’ moments, which push the object back towards the balanced position. The latter is an unstable equilibrium, where the moments act to increase the imbalance. When walking at moderate speeds, a further condition exists – a dynamic equilibrium, where from instant to instant the equilibrium is unstable but before there has been time to fall, the area of support is moved and equilibrium is restored.
The measurement of the moments generated about the joints of the lower limbs is an important part of scientific gait analysis. Such moments may be expressed in their original units (e.g. newton-metres) or they may be ‘normalised’ by dividing by body mass, changing the units to newton-metres per kilogram, to make it easier to compare results between individuals of different sizes. Although there is no general agreement on the best method of accomplishing such normalisation (Pierrynowski and Galea, 2001; Stansfield et al., 2003), it seems reasonable to normalise forces with reference to body mass and moments with reference to both body mass and either height or limb length.
Linear motion
The velocity of a moving object is the rate at which its position changes, which usually means the distance it covers in a given time. This is, of course, similar to the everyday concept of speed, except that velocity is a vector and thus has direction as well as magnitude. In measuring gait, the usual unit for velocity is metres per second, which can be abbreviated to either m/s or mċs− 1. Sometimes other units are used, such as metres per minute or kilometres per hour, but the SI units are to be preferred.
Acceleration is the rate at which velocity changes; the change may be in either magnitude or direction. An unchanging velocity has an acceleration of zero; a decrease in velocity may be known as negative acceleration, deceleration or retardation. If the velocity is measured in metres per second, the acceleration will be in metres per second per second, abbreviated to m/s2 or mċs− 2. The acceleration due to gravity has already been mentioned; it has a value of 9.81 m/s2.
The relationships between velocity, acceleration and distance travelled are given by four equations:
where u is the initial velocity (in metres per second, m/s)
v is the final velocity (in metres per second, m/s)
a is the acceleration (in metres per second per second, m/s2)
s is the distance travelled (in metres, m).
These equations help us to find unknown distances, velocities and accelerations. However all these equations assume acceleration is constant and therefore care is needed when using them in human movement and in particular gait analysis where this is seldom the case.
Circular motion
An object which is rotating has an angular velocity and if the angular velocity changes, there is an angular acceleration, such as when a wheel, rotating on its axle, either speeds up or slows down. In walking, the leg has an angular velocity and undergoes angular acceleration and retardation. Every rotating object has an angular velocity, even if it is not attached to an axle or fulcrum, and a change in that angular velocity is an angular acceleration. In the same way that linear acceleration depends on the presence of a force, angular acceleration will only occur if there is an application of a moment of force.
The detailed mathematics of angular velocity and angular acceleration are beyond the scope of this book, but it is worth saying a few words about the general concepts. Angular velocity is measured by the angle turned per unit time, usually in degrees per second or radians per second. Angular acceleration is similarly expressed in degrees (or radians) per second per second. The radian is an obscure unit to non-mathematicians; it is the ratio, within the arc of a circle, of the length of the arc to the radius of the circle. There are 2 π radians in a complete circle, giving the relationship:
When a force applied to an object produces an angular acceleration, the acceleration does not depend solely on the size of the force and the mass of the object, as it does with linear motion. It also depends on the way in which the mass is distributed about the centre of gravity, a property known as the moment of inertia. An object with the mass concentrated around the outside, such as a flywheel, has a much higher moment of inertia than one with the mass concentrated around the centre, such as a cannon ball. If a flywheel and a cannon ball have the same mass and are spinning with the same angular velocity, the flywheel will be much more difficult to stop rotating than the cannon ball, because of its higher moment of inertia.
Inertia and momentum
The term inertia is used to describe the resistance offered by a body to any attempt to set it in motion or to stop it if it is already moving. It is a descriptive term, rather than a measured physical quantity. In the case of linear motion, it results from the mass of the object; in the case of rotational motion, it results from the moment of inertia.
Momentum exists in two forms – linear and angular. The linear momentum (generally just called ‘momentum’) of a moving object is calculated by multiplying its velocity by its mass. A force applied to the object will cause it to change its velocity and hence its momentum. Another way of expressing Newton's second law is to say that the force is equal to the rate of change of momentum. The angular momentum of a rotating object is calculated by multiplying its angular velocity by its moment of inertia. A law of conservation of momentum exists, which states that momentum (both linear and angular) cannot be created or destroyed, merely transferred from one object to another.
Momentum has received little attention in gait analysis in the past but transfers of momentum are involved at a number of key events of the gait cycle, including the heelstrike transient and the end of the swing phase, both of which will be described in more detail in Chapter 2.
Kinetics and kinematics
The terms kinetics and kinematics are commonly used in gait analysis and they deserve some explanation. Kinetics is the study of forces, moments, masses and accelerations, but without any detailed knowledge of the position or orientation of the objects involved. For example, an instrument known as a force platform is used in gait analysis to measure the force beneath the foot during walking, but it gives no information on the position of the limb or the angle of the joints. Kinematics describes motion, but without reference to the forces involved. An example of a kinematic instrument is a video camera, which can be used to observe the motion of the trunk and the limbs during walking, but which gives no information on the forces involved. It is obvious that for an adequate quantitative description of an activity such as walking, both kinetic and kinematic data are needed.
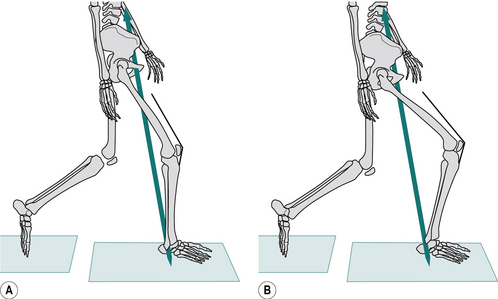
Work, energy and power
One of the remarkable features of normal gait is how energy is conserved by means of a number of optimisations. Abnormal gait patterns involve a loss of these optimisations, which may result in excessive energy expenditure and hence fatigue. The measurement, during walking, of energy transfers at individual joints and overall energy consumption is an important component of scientific gait analysis.
There is a subtle difference in viewpoint between the physical scientist and the biologist as far as work, energy and power are concerned. To the physical scientist, work is done when a force moves an object a certain distance. It is calculated as the product of the force and the distance; if a force of 2 N moves an object 3 m, the work done is:
The joule could also be called a newton-metre, but this would cause confusion with the identically named unit which is used to measure moment of force. Energy is the capacity to do work and is also measured in joules. It exists in two basic forms: potential or stored energy and kinetic or movement energy. In walking, there are alternating transfers between potential and kinetic energy, which will be described in Chapter 2. Power is the rate at which work is done; a rate of 1 J/s is a watt, which is familiar to users of electrical appliances.
The reason biologists regard these matters slightly differently from physical scientists is that muscles can use energy without shortening, in other words without doing any physical work. The potential energy stored in the muscles, in the form of ATP, is converted to mechanical energy in response to the muscle action potential. This energy is still used, even in an eccentric contraction, where the muscle actually gets longer while developing a force, which in physical terms is negative work. In other words, while everyone agrees that walking uphill involves the doing of work, the physicist might expect someone walking downhill to gain energy, whereas in reality the muscles are still activated and metabolic energy is still consumed. Even if a muscle shortens as it contracts, in a concentric contraction, the conversion of metabolic energy to mechanical energy is relatively inefficient, with a typical efficiency of around 25%. The old unit for measuring metabolic energy was the Calorie (the capital C indicating 1000 calories or 1 kilocalorie); the conversion factor is 4200 J or 4.2 kJ equals 1 Calorie (see Appendix 2).
The calculation of the mechanical power generated at joints has become an important part of the biomechanical study of gait. In a rotary movement, when a joint flexes or extends, the power is calculated as the product of the moment of force and the angular velocity, omega (ω):
In Chapter 2, reference will be made to the power exchanges across the hip, knee and ankle joints at different stages of the gait cycle. When a muscle is contracting concentrically (e.g. a flexor muscle contracts while a joint is flexing), power is generated. If a muscle contracts eccentrically (e.g. a flexor muscle contracts while a joint is extending), it absorbs power. If a muscle contracts isometrically (e.g. a flexor muscle contracts while the joint angle is unchanging), no power exchange takes place. Although, in the gait cycle, power generation and absorption are often due to muscle contraction, it is important to realise that the stretching of ligaments and other soft tissues also involves power exchange. If a ligament is stretched, it absorbs power, with a resulting storage of potential energy. Some or all of this stored energy may be released later, with a resulting power generation.
In gait analysis, it is common practice to ‘normalise’ joint power by dividing it by body mass, giving a unit of watts per kilogram, in a similar way to the treatment of joint moments (mentioned above).
Worked example
When an individual who is pain and pathology free walks, the position of the ground reaction force in relation to the knee causes a muscular response. One common gait problem is that of crouch gait which can affect several different patient groups including people with cerebral palsy. By considering the mechanics involved we are able to estimate the moments and power about the knee and the forces in the quadriceps muscles in both these conditions.
To find the moments about the knee we need to know the perpendicular distance between the ground reaction force and the knee joint and the magnitude of the ground reaction force. Figure 1.23 shows a point during loading of the front foot. In both cases the ground reaction force was 500 N. The individual who is pain and pathology free had a distance to the knee of 0.08 m and the individual with crouch gait had a distance of 0.2 m. The moment may be found by multiplying the force by the perpendicular distance. Therefore the moments will be:
To find the eccentric power we will need to know the angular velocity of the knee. If the pain and pathology-free individual has an angular velocity of 150° per second and the individual with crouch gait has an angular velocity of 40° per second, the eccentric power may be found by:
First converting degrees per second into radians per second
To find the muscle force we will need to know the knee moment and the perpendicular distance the muscle acts away from the knee joint. If in both cases the quadriceps tendon is only 0.06 m in front of the knee, the forces in the quadriceps may be found by:
Clearly crouch gait changes the mechanics and loading patterns of the knee and surrounding structures. The flexed position of the knee produces a much greater moment in the individual with crouch gait, however, they do not have the same eccentric control leading to a lower eccentric power. The increased moment at the knee has to be supported by the quadriceps but this leads to a load in the knee over two and half times that of the pain and pathology-free individual.
Duysens J., Van de Crommert H.W.A.A. Neural control of locomotion; part 1: the central pattern generator from cats to humans. Gait Posture. 1998;7:131–141.
Guyton A.C. Textbook of Medical Physiology, Twelfth ed. Philadelphia, PA: WB Saunders; 2005.
Park S., Krebs D.E., Mann W. Hip muscle co-contraction: evidence from concurrent in vivo pressure measurement and force estimation. Gait Posture. 1999;10:211–222.
Perry J. Gait Analysis: Normal and Pathological Function. Thorofare, NJ: Slack Incorporated; 1992.
Pierrynowski M.R., Galea V. Enhancing the ability of gait analyses to differentiate between groups: scaling gait data to body size. Gait Posture. 2001;13:193–201.
Pollo F.E., Jackson R.W., Komdeur P., et al. Measuring dynamic knee motion with an instrumented spatial linkage device. In: Gait and Clinical Movement Analysis Society. USA: Eighth Annual Meeting, Wilmington, Delaware; 2003:15–16.
Richards J. Biomechanics in Clinic and Research. Oxford: Churchill Livingstone; 2008.
Stansfield B.W., Hillman S.J., Hazlewood M.E., et al. Normalization of gait data in children. Gait Posture. 2003;17:81–87.