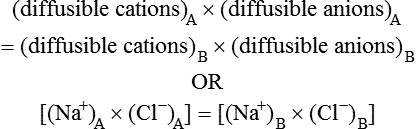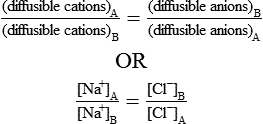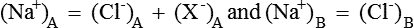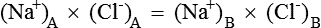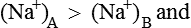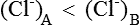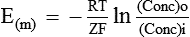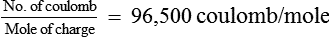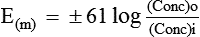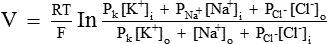Membrane Potential
Selective permeability of the cell membraneIntroduction
There exists a potential difference across the membrane of all living cells with the inside being negative in relation to the outside. This potential difference is named membrane potential, because the cations and anions arrange themselves along the outer and inner surfaces of the cell membrane. The magnitude of membrane potential varies from cell-to-cell and in a particular cell varies according to its functional status. For example, a nerve cell has a membrane potential of –70 mV (inside negative) at rest, but when it gets excited the membrane potential becomes about +30 mV (inside positive). The membrane potential at rest is called resting membrane potential or resting transmembrane potential or simply resting potential. The term rest does not imply that cell is metabolically quiescent but that it is not undergoing any electrical change. The membrane potential measured during excited state of the cell is called action potential.
Genesis of membrane potential
Membrane potential is basically due to unequal distribution of ions across the cell membrane, which in turn results due to the combined effect of various forces acting on the ions. The factors involved in genesis of membrane potential are:
• Selective permeability of the cell membrane,
• Gibbs’-Donnan membrane equilibrium,
Selective permeability of the cell membrane
The cell membrane is selectively permeable, i.e. to some ions it is freely permeable, to others impermeable and to some others it has variable permeability as:
• Ions like Na+, K+, Cl–and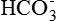 
are diffusible ions. The cell membrane is freely permeable to K+ and Cl– and moderately permeable to Na+.
• The cell membrane is practically impermeable to intra-cellular proteins and organic phosphate which are negatively charged ions.
• Presence of gated channels in the cell membrane is responsible for the variable permeability of certain ions in different circumstances.
Gibbs’-Donnan membrane equilibrium
According to Gibbs’-Donnan membrane equilibrium, when two ionized solutions are separated by a semipermeable membrane at equilibrium:
• Each solution shall be electrically neutral, i.e. total charges on cations will be equal to total charges on anions.
• The product of diffusible ions on one side of the membrane will be equal to product of diffusible ions on the other side of the membrane.
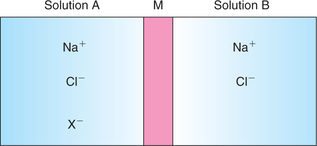
To understand let us consider ’M’ is a semipermeable membrane separating two ionized solutions of sodium chloride A and B (Fig. 1.4-1). Then according to the Gibbs’-Donnan equilibrium:
1. Each solution is electrically neutral, i.e.
2. The product of diffusible ions on both sides will be equal, i.e.
From the above equation, the ratio of diffusible ions at equilibrium will be as below:
Thus there will be symmetrical distribution of ions at equilibrium. But if one or more non-diffusible ions ‘X−’ are present on one side (A side) of the membrane, then according to Gibbs’-Donnan equilibrium the distribution of diffusible ions will be as under:
1. Both solutions will be electrically neutral, i.e.
2. The product of diffusible ions on two sides will be equal, i.e.
Hence there is unequal distribution of diffusible ions (asymmetrical). At equilibrium, Na+ being greater on the side which contains non-diffusible anions ’X ’ (side A) and anion Cl is greater on the other side (side B). However, their concentration ratio are equal.
Since the intracellular fluid (ICF) contains non-diffusible anions like proteins and organic phosphate, so, according to Gibbs’-Donnan equilibrium there should be an asymmetrical distribution of diffusible ions across the cell membrane with cations being more inside than the outside. However, in reality interior of the cell is negatively charged, which will be explained in the ensuing discussion.
Nernst equation
The asymmetrical distribution of diffusible ions across the cell membrane in the form of excess diffusible cation inside due to the Gibbs’-Donnan equilibrium (as explained above) results in concentration gradient. As a result of which diffusible cations (K+) will try to diffuse back into the extracellular fluid (ECF) from ICF, but it is counteracted by the electrical gradient, which will be created due to the presence of non-diffusible anions inside the cell. Thus, equilibrium will be reached between the concentration gradient and the electrical gradient, resulting in diffusion potential (equilibrium potential) across the cell membrane. The magnitude of this equilibrium potential can be determined by the Nernst equation as:
E(m) = Equilibrium potential (in millivolts) of the ions at which efflux and influx of the ions are equal
R = The natural gas constant and its value is 8.316 joules/ degree
F = The Faraday constant and its value is represented as
ln = Symbol for natural logarithm
(Conc)i = The concentration of the ions in the intracellular fluid (inside)
(Conc)o = The concentration of the ions in the extracellular fluid (outside)
At normal body temperature (37°C), converting from the natural log to the base 10 log and replacing some of the constants with numerical values, the equation can be simplified to:
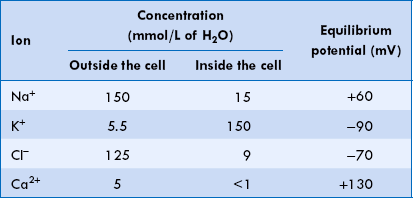
The equilibrium potential, E(m), for some of the important ions in the mammalian spinal motor neuron calculated from the simplified Nernst equation is shown in Table 1.4-1.
Goldmann-Hodgkin-Katz equation
The Nernst equation helps in calculating the equilibrium potential for each ion individually. However, the magnitude of the membrane potential at any given time depends on the distribution of Na+, K+ and Cl–, and the permeability of each of these ions. The integrated role of different ions in the generation of membrane potential can be described accurately by the Goldmann's constant field equation or the so-called Goldmann-Hodgkin-Katz (GHK) equation:
, 
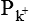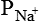and 
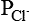= The permeabilities of the membrane to K+, Na+ and Cl–, and brackets signify concentration and i and o refer to inside and outside of the cell, respectively.
Inferences of the Goldmann constant field equation
Following important inferences can be drawn from the Goldmann's constant field equation:
1. Most important ions for development of membrane potentials in nerve and muscle fibres are sodium, potassium and chloride. The voltage of membrane potential is determined by the concentration gradient of each of these ions.
2. Degree of importance of each of the ions in determining the voltage depends upon the membrane permeability of the individual ion. For example, if the membrane is impermeable to K+ and Cl- then the membrane potential will be determined by the Na+ gradient alone and the resulting potential will be equal to the Nernst potential for sodium.
3. Positive ion concentration from inside the membrane to outside is responsible for electronegativity inside the membrane. This is because of the fact that due to concentration gradient, the positive ions diffuse outside leaving the non-diffusible negative ions inside the cell.
4. Signal transmission in the nerves is primarily due to change in the sodium and potassium permeability because their channels undergo rapid change during conduction of the nerve impulse and not much change is seen in the chloride channels.
Role of NA+-K+ ATPase pump
The role of Na+-K+ ATPase lies in building the concentration gradient. It serves to pump back the Na+ that diffuses into the cell and K+ that diffuses out of the cell. In the resting membrane, these diffusions are negligible, so the Na+-K+pump works very feebly in this stage. Further, although the Na+-K+ pump is potentially electrogenic (since it pumps out 3Na+ ions for 2K+ ions), at no stage the pump is able to build up a significant membrane potential. This is because of the fact that as soon as the pump creates a negative potential inside the cell, chloride ions rush out of the cell and restore electroneutrality. Thus, in other words, the pump pumps out 3Na+ ions and one Cl– ion for every 2K+ ions it pumps in.
Recording of membrane potential
Instruments used for recording
The essential instruments used in recording the activity of an excitable tissue are:
Basic principles of the functioning of these instruments are described on page 38.