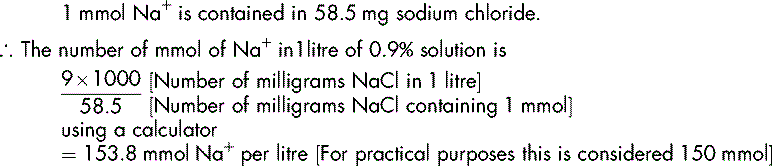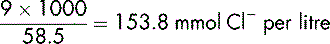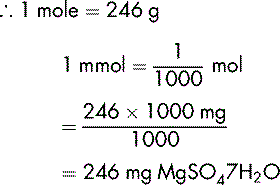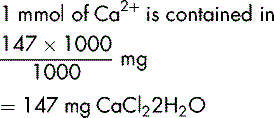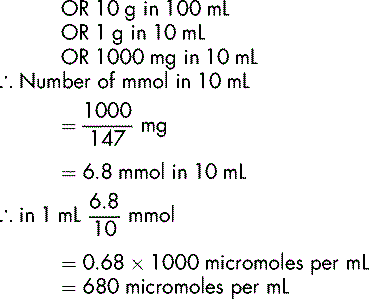CHAPTER 6 Calculating parenteral doses
large volume
Introduction
Water makes up between 50% and 70% body weight. Most body processes are dependent on water. Movement of a wide range of substances round the body depends on water (e.g. nutrients, hormones, electrolytes, and waste products).
Fluid losses, mainly through the kidney, must be replaced, in normal circumstances, by drinking (about 2 litres per day).
When the fluid balance of the body is compromised by, say, diarrhoea, vomiting or trauma (burns) and the oral route cannot be used, fluids and electrolytes are administered parenterally (Sexton and Rahman 2008).
Intravenous infusions are widely used with great benefit for patients. Nurses play a key role in the safe management of fluid and electrolyte therapy.
Many body processes depend on electrical activity at the cellular level, e.g. the passage of a nerve impulse. This electrical activity is made possible by the presence of electrolytes, mainly sodium, potassium and calcium in cells and plasma. An electrolyte can be defined as a chemical substance that dissociates in water to yield electrically charged particles known as ions. Sodium chloride dissociates in water to yield Na+ (cation) and Cl− (anion)
Intravenous infusions
Special points
Practice aspects
Products
The more common solutions used for intravenous infusion (large volumes) are listed in Table 6.1. The information on a typical infusion solution bag is shown in Figs. 6.1-6.3. Nurses have to be ready to interpret common abbreviations and chemical symbols (see Abbreviations). Normal volumes in containers are 100 mL, 500 mL and 1000 mL.
Table 6.1 Common infusion solutions
| Active ingredient of solution | Content and common strengths w/v | Notes |
|---|---|---|
| Glucose (dextrose anhydrous) | 5% | Commonly used solution to replace water deficit |
| Energy source | ||
| Potassium chloride | Potassium chloride 0.3% or 0.15% with 5% glucose | Used to correct hypokalaemia. In view of dangers of overdose, use ready made up solution rather than add a concentrated solution to an infusion solution. |
| Sodium bicarbonate | Used to control severe metabolic acidosis | |
| Sodium chloride | 0.9% (normal saline) often in combination with glucose and other electrolytes | Used for electrolyte/water imbalance and as a vehicle for drug administration |
| Sodium lactate compound infusion | Sodium chloride, sodium lactate, potassium chloride, calcium chloride (see BNF for details) (BMA and RPSGB 2009) | Used for electrolyte and water deficiency |
Administration
Infusions are administered using an administration set which conveys the fluid from the bag either to a cannula already sited in a peripheral vein or by central venous access. Administration sets vary depending on whether the infusion is to be administered by gravity or by pump and whether the infusion is of a clear fluid or of blood. It is essential to select the appropriate set as the rate of flow has been predetermined in the different types available.
For adults, the set to use for:
If there is any doubt about which set to use, reference should be made to the administration set packaging.
The safest way to administer an intravenous infusion is to deliver it via an infusion pump, as this method provides very precise control over the rate of the fluid. Where large volumes are to be given or where the fluid and/or its contents are highly potent, the standard expected would involve the use of an infusion pump. However, infusion pumps are costly, and it may not be possible to provide one in every case. It is obvious therefore that nurses are required to be competent in managing infusions with or without an infusion pump.
Gravity-assisted infusion
An infusion may be set up which simply allows the fluid to travel from the bag through the administration set to the cannula or by central venous access under the influence of gravity. With this type of infusion, the rate of fluid can be controlled in three ways. These are the:
To calculate how to set the infusion at the prescribed rate, you need to know the amount to be infused and the length of time the infusion is to take. The next step is to work out how much will be infused in 1 hour. This is done by dividing the total volume by the time the infusion is to take:
For example, 500 mL of a clear fluid is to be transfused over 4 hours:
The prescribed rate is 125 mL/h.
In order that the infusion can be regulated, however, the nurse needs to know how many drops per minute at which to set the infusion. In this instance, a clear solution is in use and therefore the appropriate administration set would be one set at 20 drops/mL.
To calculate the rate of flow in drops per minute, which the nurse will be able to count using a watch:
The infusion can be controlled at 42 drops per minute.
Some prescription sheets provide a ready reckoner to assist the nurse in calculating the rate of flow and should be used where provided.
Since other variables come into play, such as the positioning of the patient which may increase the flow rate, this method is not wholly reliable, and so to limit the risks associated with the infusion of large volumes of fluid, the maximum size of bag used is often limited to 500 mL.
Pump-assisted infusion
When using an infusion pump (Fig. 6.4), the appropriate administration set (specifically for use with a pump) must be used.
The infusion pump has been designed to provide very precise control of the rate at which the fluid is infused. It does not serve the purpose of a calculator and so it is essential to know how to calculate what the patient is to receive, i.e. the flow rate. This is expressed in millilitres per hour (mL/h).
Once the calculation has been made, and only then, the rate and the total volume to be infused can be keyed in to the pump.
To calculate the flow rate, the prescribed volume (always in mL) is divided by the duration of the infusion (always per hour):
If a volume of 1000 mL is to be infused over 8 hours, it can be represented as:
The rate is therefore 125 mL per hour.
These figures are then carefully entered using the appropriate keys. The pump will not correct any errors made; it will only perform on the basis of the information that has been entered into it. Over-reliance on it is to be avoided and periodic checks (e.g. at least hourly) must be made to ensure that the amount infused and the amount left, when added together, are the same as the original volume to be infused.
Reconstitution and dilution of parenteral medicines
Some parenteral medicines may need to be reconstituted, by adding a suitable volume of a diluent and then being further diluted for administration. Often dilution is required because of the irritancy of the drug to the tissues. Whenever possible, dilution to the required strength should be undertaken in a controlled environment (in pharmacy) in order to minimise the risk of microbial contamination. The BNF gives details of any necessary dilutions. The dilution will depend on the method of administration (Table 6.2), i.e.:
Table 6.2 Examples of diluents
| Method | Drug | Diluent |
|---|---|---|
| Continuous | Danaparoid | Sodium chloride 0.9% or glucose 5% |
| Intermittent | Carmustine | Sodium chloride 0.9% or glucose 5% |
| Via drip tubing | Epirubicin | Sodium chloride 0.9% or water for injections |
The choice of method used will depend on a number of factors including clinical factors and the stability of the drug added to the infusion. The calculations and procedures involved are essentially the same as with small-volume parenterals (see Chapter 5).
Essentially, very similar calculations are involved when administering intermittent infusions except that the volume involved will be smaller than in continuous infusions.
The method chosen will depend on the patient’s condition and the chemical, physical and pharmacological properties of the drug.
Calculation of dilute solutions for infusion
Demonstration 6.1
Dopexamine is to be diluted in glucose 5% to produce a solution containing 400 micrograms in 1 mL. To prepare 500 mL of the dilute solution, the total amount of dopexamine required is:
The solution available for dilution contains 10 mg in 1 mL in 5 mL ampoules (or 50 mg in 5 mL).
20 mL must be diluted to 500 mL to provide a solution containing 400 micrograms in 1 mL.
Demonstration 6.2
Salbutamol solution for infusion (for bronchodilatation) should contain 200 micrograms in 1 mL. To prepare 200 mL (in glucose 5%) of the dilute solution, the total amount of salbutamol required is:
The solution available for dilution contains 1 mg/1 mL in 5 mL ampoules (or 5 mg in 5 mL).
Transfusion of blood and blood components
It is essential when administering blood or its components to use the correct administration set, normally one that delivers 15 drops/minute. The volume in each bag of blood varies and so it is important to read the accompanying blood prescription form and the label on the bag to establish the exact volume. A bag of red cells may contain anything from 260 mL to 300 mL; for example, the figure could be 268 mL. If the bag is to be transfused in 3 hours, to calculate the flow rate, the volume, as before, must be divided by the duration:
To calculate the number of drops per minute, 1.489 is multiplied by 15 (remember, the administration set used for blood transfusion is set at 15 drops per mL):
An example such as this one should be checked using a calculator.
Blood may also be administered using a pressure bag or rapid infuser via large-bore central access allowing the administration of a unit of blood in a few seconds. Rapid infusers are commonly used in theatre, maternity and intensive care environments.
Subcutaneous infusion (by hypodermoclysis)
A number of medicines can be infused into the body by the subcutaneous route; the administration of a subcutaneous infusion can be established and maintained by the nurse. The introduction of fluid into the patient by this method is dependent on gravity; there is no need for an infusion pump to be used. Alternatively, a syringe driver may be used.
Clear fluids are always used and so the administration set is always the same, i.e. one that is set at 20 drops per mL. Calculating the flow rate is exactly the same as for a gravity-assisted intravenous infusion (see pp. 114–115).
Exercises of large-volume parenteral infusion calculations to practise
The calculations in this section are presented in a different format to that of earlier chapters. Because the prescribing documentation and calculations are very varied, the levels classification system used earlier is not appropriate. All the essential information is given to enable the calculations to be completed using the methods covered in the text. Unless otherwise stated, the diluent is glucose 5%. Answers are given on p. 195.
Exercise 6.1
| Prescription/other clinical data | Product details | Commentary |
|---|---|---|
| Soluble insulin (human) 50 units in 50 mL 0.9% sodium chloride solution (for use in syringe driver) | Soluble insulin (human) 100 units/1 mL | Take particular care to select the correct product |
Exercise 6.2
| Prescription/other clinical data | Product details | Commentary |
|---|---|---|
| Dopamine 260 mg IV to be diluted to 1.6 mg/mL in glucose 5% solution | Dopamine injection 40 mg/1 mL (in 5 mL ampoules) | An inotropic sympathomimetic |
Exercise 6.3
| Prescription/other clinical data | Product details | Commentary |
|---|---|---|
| Sodium bicarbonate 50 mmol by IV injection | Sodium bicarbonate 1.26% w/v sterile solution containing 150 mmol each of Na+ and HCO3− per litre | Used to treat severe metabolic acidosis |
| What is the total volume (mL) of sodium bicarbonate solution to be infused? | ||
Exercise 6.4
| Prescription/other clinical data | Product details | Commentary |
|---|---|---|
| Digoxin 750 micrograms IV to be given over a 2 hour period diluted in 50 mL glucose 5% solution | Digoxin injection 250 micrograms/1 mL in 2 mL ampoules | A cardiac glycoside |
Exercise 6.5
| Prescription/other clinical data | Product details | Commentary |
|---|---|---|
| Lidocaine 1 mg/min by IV infusion | Lidocaine 1 g in 500 mL glucose 5% w/v solution | Lidocaine is used in the treatment of arrhythmias |
| Calculate the flow rate in mL/hour | ||
Exercise 6.6
| Prescription/other clinical data | Product details | Commentary |
|---|---|---|
| Aminophylline 500 micrograms/kg/hour by IV infusion | Aminophylline 250 mg in 500 mL sodium chloride solution 0.9% | |
Exercise 6.7
| Prescription/other clinical data | Product details | Commentary |
|---|---|---|
| Vasopressin 0.2 unit/mL to be given over 15 min IV | Synthetic vasopressin injection 20 units/mL in 1 mL ampoules | Vasopressin is an antidiuretic hormone used to treat pituitary diabetes insipidus |
| Calculate the volume (mL) of vasopressin injection to be diluted in 100 mL | ||
Exercise 6.8
| Prescription/other clinical data | Product details | Commentary |
|---|---|---|
| Heparin 500 units/1 mL in 50 mL glucose solution 5% by continuous infusion | Heparin injection 25 000 units/1 mL ampoules | Heparin is an anticoagulant |
| Calculate the total quantity (mL) of heparin injection to be diluted to 50 mL | ||
Exercise 6.9
| Prescription/other clinical data | Product details | Commentary |
|---|---|---|
| Adrenaline (epinephrine) 50 mL of a 1 in 10 000 solution infused IV at 5 mL/hour | Adrenaline 1 in 10 000 injection | Adrenaline (epinephrine) is a non-selective alpha and beta receptor agonist used in the emergency treatment of hypotension, anaphylaxis and angioedema |
| How much adrenaline (micrograms) is infused per hour? | ||
Exercises 6.10-6.12 are not based on prescriptions but are included as an aid to understanding percentages.
Critical care
Of all the patient care specialities, few are as complex and demanding as critical care. A thorough knowledge of physiology, pathophysiology and pharmacology is required. Practitioners have to deal with daily unpredictability and act efficiently, effectively and decisively.
Management of medicines in a critically ill patient is a complex task requiring knowledge of drug therapy in acute and chronic disease states. The risks associated with drug therapy are higher than elsewhere. Multiple prescribing is commonplace. High doses are often prescribed increasing the risks.
Rapid action needs to be taken and a rapid response achieved. The patient may be receiving multiple intravenous infusions at the same time along with frequent boluses and intermittent infusions. These infusions often include high-risk drugs and errors in prescription, calculation, administration or delivery, as well as interactions can occur.
Drug calculations in critical care are carried out in a very demanding environment where speed and accuracy are essential and therefore it is important to have calculations checked.
Further exercises
Intravenous nutrition
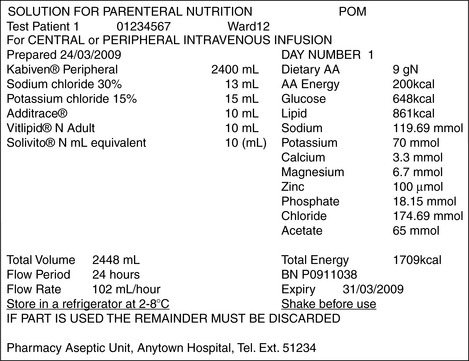
When disease or trauma involving the alimentary tract makes adequate nutrition impossible, supplementary or total parenteral nutrition (TPN) will often be required. Solutions containing essential and non-essential amino acids (protein source), carbohydrate and fat (energy sources), electrolytes, trace elements and vitamins are widely used. Nurses will not normally be involved in calculating the amounts of the various components to be combined to produce the solution that best meets the patient’s needs; the special solutions will normally be formulated and prepared in the pharmacy. However, the nurse needs to be aware of the physiological needs of the patient as expressed in appropriate units and must be capable of interpreting the information given on the label of the container (see Fig. 6.5).
Energy requirements
The units used to indicate the energy content of solutions used for intravenous nutrition (and other nutritional products) are as follows:
TPN solutions are formulated so that there is a balance between the amount of energy and protein (in the form of amino acids). The BNF recommends that energy be provided in a ratio of 0.6 to 1.1 mJ per gram of protein nitrogen. Energy is provided by a carbohydrate (glucose is the preferred source) and emulsified fat which has a high energy content.
Further exercises
Elements, atoms, molecules, moles, micromoles and millimoles
Many large-volume solutions for intravenous infusion including TPN solutions contain electrolytes and trace elements. The content of electrolytes and trace elements in a solution is normally expressed in millimoles or micromoles in a given volume (see pp. 126–128).
Elements
All matter is made up of elements either individually or in combination. Examples of elements are hydrogen, oxygen, carbon, sodium, calcium, chlorine, iron, silver, magnesium and gold. Diamond and graphite comprise a single element carbon, whereas water is a combination of two elements, hydrogen and oxygen (H2O).
Atoms
All elements are made up from atoms. An atom is the smallest particle into which an element can be divided. The atom is made up of a central nucleus containing protons (positively charged) and neutrons (with no charge). The electrons (negatively charged) revolve around the nucleus of the atom in orbits or shells. The atomic number of an element is the number of protons in the nucleus of an atom. The mass number of an element is the sum of the number of protons and neutrons in the nucleus of an atom. As the number of protons and neutrons differs, each element will have a different atomic weight and mass number (Table 6.3).
Table 6.3 Atoms and masses (weights)
| Atom | Chemical symbol | Mass |
|---|---|---|
| Bicarbonate | HCO3 | 61 |
| Calcium | Ca | 40 |
| Carbon | C | 12 |
| Chlorine | Cl | 35.5 |
| Hydrogen | H | 1 |
| Magnesium | Mg | 24 |
| Oxygen | O | 16 |
| Potassium | K | 39 |
| Sodium | Na | 23 |
Molecules
A molecule is a combination of two or more atoms that are held together by bonds. Molecules may contain two atoms of the same element such as oxygen (O2) or they may consist of two or more different atoms such as calcium and chlorine (CaCl2 – calcium chloride) and hydrogen and oxygen (H2O – water). The molecular mass of a molecule is calculated by adding the atomic weights (mass numbers), e.g. sodium – Na (atomic weight 23) combines with chlorine – Cl (atomic weight 35.5) to form sodium chloride. Sodium chloride has a molecular mass of 58.5 (the sum of the atomic weights).
Avogadro’s number and the mole
In 1811, the Italian scientist Amadeo Avogadro (1766–1856) first put forward the concept that the volume of a gas (at a given temperature and pressure) is proportional to the number of atoms or molecules regardless of the nature of the gas. The concept was developed over the years by scientists and a number was determined. This number was named in honour of Avogadro in 1909. You may be forgiven for wondering what this has to do with the nurse in clinical practice, especially when the number (which Avogadro never knew) is revealed. The number is 6.022137 x 1023. Clearly this is a VERY, VERY large number indeed. When dealing with atoms, however, the numbers are VERY, VERY large, and it is essential that chemists are able to deal with these numbers. Chemists count atoms by weighing them, and the results of their calculations are used in clinical practice.
The mole (mol) is the amount of substance which contains as many elementary entities as there are atoms in 0.012 kilograms (12 g) of carbon (C12). The number of atoms is 6.022137 x 1023, i.e. Avogadro’s number (N-A). This definition will probably not have much resonance with non-chemists. Nevertheless, the mole and the units derived from it are of considerable practical importance in clinical practice.
In practical terms, a mole (mol) can be considered as the molecular mass of the substance expressed in grams. When 1 mole of a substance is dissolved in 1 litre of water (or other solvent), a molar solution is produced. As will be seen in Table 6.4, molar solutions are of a high concentration which seldom, if ever, have direct clinical applications.
Table 6.4 Moles and millimoles
| One mole of substance (chemical symbol) | Molecular mass (g) |
|---|---|
| Calcium chloride dihydrate (CaCl22H2O) | 147 g (40 + 71 + 36) |
| Magnesium sulphate heptahydrate (MgSO47H2O) | 246 g (120 + 126) |
| Potassium chloride (KCl) | 74.5 g (39 + 35.5) |
| Sodium bicarbonate (NaHCO3) | 84 g (23 + 61) |
| Sodium chloride (NaCl) | 58.5 g (23 + 35.5) |
Having defined (at some length!) the mole, we can now define two more practical units, the millimole (mmol) and the micromole. These units are widely used in biochemistry and parenteral therapy.
We have seen that 1 mole of sodium chloride (NaCl) is equivalent to 58.5 g.
It follows that 1 mmol of sodium chloride is equal to 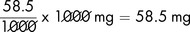 .
.
Sodium chloride is a molecule that contains both sodium and chloride. 1 mmol of sodium chloride (NaCl) contains 1 mmol of sodium (Na+) and 1 mmol of chloride (Cl−).
The usual strength of sodium chloride intravenous infusion is 0.9% w/v (normal saline). Given this information and the fact that the molecular mass of sodium chloride is 58.5 g, we can calculate the number of millimoles of sodium (Na+) and chloride (Cl−) in a given volume (1 litre) of normal saline.
Demonstration 6.3
Physiological saline contains 0.9% w/v sodium chloride
Calculate the number of mmol of sodium (Na+) in 1 litre of the solution.
Demonstration 6.4
The same calculation can be used to determine the chloride content.
Given that the chemical formula of sodium chloride is NaCl, it follows that each mmol of sodium chloride contains 1 mmol of chloride (Cl−). The calculation is the same as Demonstration 6.3.
A formula can be used for this and similar calculations but it is generally better to work from first principles.
Micromoles
In some instances, the amount of a substance, e.g. a trace element present in a solution is very small. The micromole, or 1/1000 millimole, is used to express the concentration of a substance in a given volume, e.g. a calcium chloride dihydrate 10% w/v solution contains 680 micromol/mL, an injection of zinc sulphate 14.6 mg per mL contains 50 micromol/mL.
Demonstration 6.6
Calculate the number of micromoles per mL of Mg2+ of a 20% w/v injection of magnesium sulphate hexahydrate MgSO47H2O.
This has a molecular mass of 246.
Further exercises
(Note – It is important that the sterile potassium concentrate is diluted with not less than 50 times its volume of sodium chloride intravenous infusion and mixed well.)
Although most instances where the nurse will encounter mmols will be in connection with intravenous therapy, there are instances when millimoles are used in expressing the strength of oral therapy. Two examples follow.
BMA (British Medical Association) and RPSGB (Royal Pharmaceutical Society of Great Britain). British National Formulary. London: BMJ Group and RPS Publishing, 2009.
NHS NPSA. Rapid Response Report. London: NHS National Patient Safety Agency, 2008.
Sexton J., Rahman M.H. Parenteral replacement of fluids and electrolytes: the basics. The Pharmaceutical Journal. 2008;281:571-574.



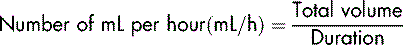


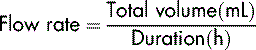
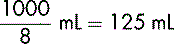
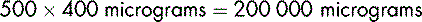
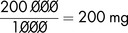
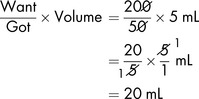
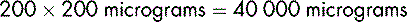
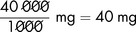
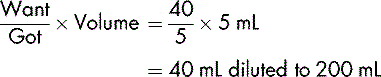
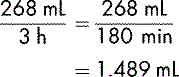

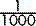 of a mole.
of a mole.