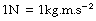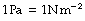Appendix A Physical quantities and units of measurement
SI Units
A clean transition from the old to the new metric units failed to occur. The old system was based on the centimetre-gram-second (CGS) and was supplemented with many non-coherent derived units such as the millimetre of mercury for pressure and the calorie for work, which could not be related to the basic units by factors which were powers of ten. The new system, the Système Internationale or SI, is based on the metre-kilogram-second (MKS) and comprises base and derived units which are obtained simply by multiplication or division without the introduction of numbers, not even powers of ten.1
Base units are metre (length), kilogram (mass), second (time), ampere (electric current), kelvin (thermodynamic temperature), mole (amount of substance) and candela (luminous intensity).
Derived units include newton (force: kilograms metre second−2), pascal (pressure: newton metre−2), joule (work: newton metre) and hertz (periodic frequency: second−1).
Special non-SI units are recognised as having sufficient practical importance to warrant retention for general or specialised use. These include litre, day, hour, minute and the standard atmosphere.
Non-recommended units include the dyne, bar, calorie and gravity-dependent units such as the kilogram-force, centimetre of water and millimetre of mercury, the demise of which has been expected for many years.
The use of SI units in respiratory physiology and clinical practice remains incomplete. The kilopascal has replaced the millimetre of mercury for blood gas partial pressures in Europe but the old units continue to be used in the USA and Australasia. The introduction of the kilopascal for fluid pressures in the medical field has failed to occur for, what appears to be, an entirely specious attachment to the mercury or water manometer. We appear to be condemned to a further period during which we record arterial pressure in mmHg and venous pressure in cmH2O. This absurd situation would be less dangerous if all staff knew the relationship between a millimetre of mercury and a centimetre of water.
As in previous editions of this book, it has proved necessary to make text and figures bilingual, with both SI and CGS units for the benefit of readers who are unfamiliar with one or other of the systems. Some useful conversion factors are listed in Table A.1. There are still some areas of physiology and medicine where non-SI units continue to be extensively used, such as mmHg for most vascular pressures and centimetres of water for airway pressure, so these units are retained throughout this book to aid clarity.
Table A.1 Conversion factors for units of measurement
| Force | |
| 1 N (newton) | = 105 dyn |
| Pressure | |
| 1 kPa (kilopascal) | = 7.50 mmHg = 10.2 cmH2O = 0.009 87 standard atmospheres = 10 000 dyn.cm−2 |
| 1 standard atmosphere | = 101.3 kPa = 760 mmHg = 1033 cmH2O = 10 m of sea water (S.G. 1.033) |
| 1 mmHg | = 1.36 cmH2O = 1 torr (approx) |
| Compliance | |
| 1 l.kPa−1 | = 0.098 l.cmH2O−1 |
| Flow resistance | |
| 1 kPa.l−1.s | = 10.2 cmH2O.l−1.sec |
| Work | |
| 1 J (joule) | = 0.102 kilopond metres = 0.239 calories |
| Power | |
| 1 W (watt) | = 1 J.s−1 = 6.12 kp.m.min−1 |
| Surface tension | |
| 1 N.m−1 (Newton/metre or pascal metre) | = 1000 dyn.cm−1 |
In the Figures, Tables and text of this book 1 kPa has been taken to equal 7.5 mmHg or 10 cmH2O.
Physical quantities relevant to respiratory physiology are defined below, together with their mass/length/time (MLT) units. These units provide a most useful check of the validity of equations and other expressions which are derived in the course of studies of respiratory function. Only quantities with identical MLT units can be added or subtracted and the units must be the same on both sides of an equation.
Volume (Dimensions: L3)
In this book we are concerned with volumes of blood and gas. Strict SI units would be cubic metres and submultiples. However, the litre (l) and millilitre (ml) are recognised as special non-SI units and will remain in use. For practical purposes, we may ignore changes in the volume of liquids which are caused by changes of temperature. However, the changes in volume of gases caused by changes of temperature or pressure are by no means negligible and constitute an important source of error if they are ignored. These are discussed in detail in Appendix C.
Fluid Flow Rate (Dimensions: L3/T, OR L3.T−1)
In the case of liquids, flow rate is the physical quantity of cardiac output, regional blood flow, etc. The strict SI units would be metre3.second−1, but litres per minute (l.min−1) and millilitres per minute (ml.min−1) are special non-SI units which may be retained. For gases, the dimension is applied to minute volume of respiration, alveolar ventilation, peak expiratory flow rate, oxygen consumption, etc. The units are the same as those for liquids except that litres per second are used for the high instantaneous flow rates that occur during the course of inspiration and expiration.
In the case of gas flow rates, just as much attention should be paid to the matter of temperature and pressure as when volumes are being measured (Appendix C).
Force (Dimensions: MLT−2)
Force is defined as mass times acceleration. An understanding of the units of force is essential to an understanding of the units of pressure. Force, when applied to a free body, causes it to change either the magnitude or the direction of its velocity.
The units of force are of two types. The first is the force resulting from the action of gravity on a mass and is synonymous with weight. It includes the kilogram-force and the pound-force (as in the pound per square inch). All such units are non-recommended under the SI and have almost disappeared. The second type of unit of force is absolute and does not depend on the magnitude of the gravitational field. In the CGS system, the absolute unit of force was the dyne and this has been replaced under the MKS system and the SI by the newton (N), which is defined as the force which will give a mass of 1 kilogram an acceleration of 1 metre per second per second.
Pressure (Dimensions: MLT−2/L2, OR ML−1T−2)
Pressure is defined as force per unit area. The SI unit is the pascal (Pa) which is 1 newton per square metre.
The pascal is inconveniently small (one hundred-thousandth of an atmosphere) and the kilopascal (kPa) has been adopted for general use in the medical field. Its introduction is simplified by the fact that the kPa is very close to 1% of an atmosphere. Thus a standard atmosphere is 101.3 kPa and the Po2 of dry air is very close to 21 kPa.
The standard atmosphere may continue to be used under SI. It is defined as 1.013 25 × 105 pascals.
The torr came into use only shortly before the move towards SI units. This is unfortunate for the memory of Torricelli, as the torr will disappear from use. The torr is defined as exactly equal to 1/760 of a standard atmosphere and it is therefore very close to the millimetre of mercury, the two units being considered identical for practical purposes. The only distinction is that the torr is absolute, while the millimetre of mercury is gravity based.
The bar is the absolute unit of pressure in the old CGS system and is defined as 106 dyn.cm−2. The unit was convenient because the bar is close to 1 atmosphere (1.013 bars) and a millibar is close to 1 centimetre of water (0.9806 millibars).
Compliance (Dimensions: M−1L4T2)
The term ‘compliance’ is used in respiratory physiology to denote the volume change of the lungs in response to a change of pressure. The dimensions are therefore volume divided by pressure, and the commonest units have been litres (or millilitres) per centimetre of water. This continues to slowly change over to litres per kilopascal (l.kPa−1).
Resistance to Fluid Flow (Dimensions: ML−4T−1)
Under conditions of laminar flow (see Figure 4.2) it is possible to express resistance to gas flow as the ratio of pressure difference to gas flow rate. This is analogous to electrical resistance, which is expressed as the ratio of potential difference to current flow. The dimensions of resistance to gas flow are pressure difference divided by gas flow rate, and typical units in the respiratory field have been cmH2O per litre per second (cmH2O.l−1.s) or dynes.sec.cm−5 in absolute units. Appropriate SI units will probably be kPa.l−1.s.
Work (Dimensions: ML2T−2, Derived from MLT−2 × L or ML−1T−2 × L3)
Work is done when a force moves its point of application or gas is moved in response to a pressure gradient. The dimensions are therefore either force times distance or pressure times volume, in each case simplifying to ML2T−2. The multiplicity of units of work has caused confusion in the past. Under SI, the erg, calorie and kilopond-metre will disappear in favour of the joule, which is defined as the work done when a force of 1 newton moves its point of application 1 metre. It is also the work done when 1 litre of gas moves in response to a pressure gradient of 1 kilopascal. This represents a welcome simplification.
Power (Dimensions: ML2T−2/T or ML2T−3)
Power is the rate at which work is done and so has the dimensions of work divided by time. The SI unit is the watt, which equals 1 joule per second. Power is the correct dimension for the rate of continuous expenditure of biological energy, although one talks loosely about the ‘work of breathing’. This is incorrect and ‘power of breathing’ is the correct term.