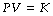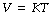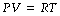Appendix B The gas laws
A knowledge of physics is more important to the understanding of the respiratory system than of any other system of the body. Not only gas transfer but also ventilation and perfusion of the lungs occur largely in response to physical forces, with vital processes playing a less conspicuous role than is the case, for example, in brain, heart or kidney.
Certain physical attributes of gases are customarily presented under the general heading of the gas laws. These are of fundamental importance in respiratory physiology.
Boyle’s law describes the inverse relationship between the volume and absolute pressure of a perfect gas at constant temperature:
where P represents pressure and V represents volume. At temperatures near their boiling point, gases deviate from Boyle’s law. At room temperature, the deviation is negligible for oxygen and nitrogen and of little practical importance for carbon dioxide or nitrous oxide.
Charles’ law describes the direct relationship between the volume and absolute temperature of a perfect gas at constant pressure:
where T represents the absolute temperature. There are appreciable deviations at temperatures immediately above the boiling point of gases. Equations (1) and (2) may be combined as:
where R is the universal gas constant, which is the same for all perfect gases and has the value of 8.1314 joules.degrees kelvin−1.moles−1. From this it may be derived that the mole volume of all perfect gases is 22.4 litres at standard temperature and pressure, dry (STPD). Carbon dioxide and nitrous oxide deviate from the behaviour of perfect gases to the extent of having mole volumes of about 22.2 litres at STPD.
Henry’s law describes the solution of gases in liquids with which they do not react. The general principle of Henry’s law is simple enough. The number of molecules of gas dissolving in the solvent is directly proportional to the partial pressure of the gas at the surface of the liquid, and the constant of proportionality is an expression of the solubility of the gas in the liquid. This is a constant for a particular gas and a particular liquid at a particular temperature but usually falls with rising temperature.
Unfortunately, confusion often arises from the multiplicity of units that are used. For example, when considering oxygen dissolved in blood, it has been customary to consider the amount of gas dissolved in units of vols% (ml of gas at STPD per 100 ml blood) and the pressure in mmHg. Solubility is then expressed as vols% per mmHg, the value for oxygen in blood at 37°C being about 0.003. However, for carbon dioxide in blood, we tend to use units of mmol.l−1 of carbon dioxide per mmHg. The units are then mmol.l−1.mmHg−1, the value for carbon dioxide in blood at 37°C being 0.03. Both vols% and mmol.l−1 are valid measurements of the quantity (mass or number of molecules) of the gas in solution and are interchangeable with the appropriate conversion factor.
Physicists are more inclined to express solubility in terms of the Bunsen coefficient. For this, the amount of gas in solution is expressed in terms of volume of gas (STPD) per unit volume of solvent (i.e. one-hundredth of the amount expressed as vols%) and the pressure is expressed in atmospheres.
Biologists, on the other hand, prefer to use the Ostwald coefficient. This is the volume of gas dissolved, expressed as its volume under the conditions of temperature and pressure at which solution took place. It might be thought that this would vary with the pressure in the gas phase, but this is not so. If the pressure is doubled, according to Henry’s law, twice as many molecules of gas dissolve. However, according to Boyle’s law, they would occupy half the volume at double the pressure. Therefore, if Henry’s and Boyle’s laws are obeyed, the Ostwald coefficient will be independent of changes in pressure at which solution occurs. It will differ from the Bunsen coefficient only because the gas volume is expressed as the volume it would occupy at the temperature of the experiment rather than at 0°C. Conversion is thus in accord with Charles’ law and the two coefficients will be identical at 0°C. This should not be confused with the fact that, like the Bunsen coefficient, the Ostwald coefficient falls with rising temperature.
The partition coefficient is the ratio of the number of molecules of gas in one phase to the number of molecules of gas in another phase when equilibrium between the two has been attained. If one phase is gas and the other liquid, the liquid/gas partition coefficient will be identical to the Ostwald coefficient. Partition coefficients are also used to describe partitioning between two media (e.g. oil/water, brain/blood, etc.).
Graham’s law of diffusion governs the influence of molecular weight on the diffusion of a gas through a gas mixture. Diffusion rates through orifices or through porous plates are inversely proportional to the square root of the molecular weight. This factor is only of importance in the gaseous part of the pathway between ambient air and the tissues, and is, in general, only of importance when the molecular weight is greater than that of oxygen or carbon dioxide. Graham’s law is not relevant to the process of ‘diffusion’ through the alveolar/capillary membrane (page 147).
Dalton’s law of partial pressure states that, in a mixture of gases, each gas exerts the pressure that it would exert if it occupied the volume alone (see Figure 13.8). This pressure is known as the partial pressure (or tension) and the sum of the partial pressures equals the total pressure of the mixture. Thus, in a mixture of 5% carbon dioxide in oxygen at a total pressure of 101 kPa (760 mmHg), the carbon dioxide exerts a partial pressure of 5/100 × 101 = 5.05 kPa (38 mmHg). In general terms:
In the alveolar gas at sea level, there is about 6.2% water vapour, which exerts a partial pressure of 6.3 kPa (47 mmHg). The available pressure for other gases is therefore (Pb−6.3) kPa or (Pb−47) mmHg. Gas concentrations are usually measured in the dry gas phase and therefore it is necessary to apply this correction for water vapour in the lungs.