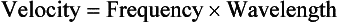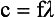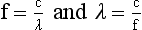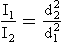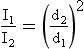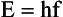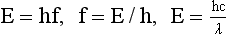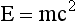Electromagnetic Energy
At the completion of this chapter, the student should be able to do the following:
1 Identify the properties of photons.
2 Explain the inverse square law.
PHOTONS WERE first described by the ancient Greeks. Today, photons are known as electromagnetic energy; however, these words are commonly used interchangeably. Electromagnetic energy is present everywhere and exists over a wide energy range. X-rays, visible light, and radiofrequencies are examples of electromagnetic energy.
The properties of electromagnetic energy include frequency, wavelength, velocity, and amplitude. In this chapter, discussions of visible light, radiofrequency (RF), and ionizing radiation highlight these properties and the importance of electromagnetic energy in medical imaging. The wave equation and the inverse square law are mathematical formulas that further describe how electromagnetic energy behaves.
The wave-particle duality of electromagnetic energy is introduced as wave theory and quantum theory. Matter and energy, as well as their importance to medical imaging, are summarized.
Photons
Ever present all around us is a field or state of energy called electromagnetic energy. This energy exists over a wide range called an energy continuum. A continuum is an uninterrupted (continuous) ordered sequence. Examples of continuums are free-flowing rivers and sidewalks. If the river is dammed or the sidewalk curbed, then the continuum is interrupted. Only an extremely small segment of the electromagnetic energy continuum—the visible light segment—is naturally apparent to us.
The ancient Greeks recognized the unique nature of light. It was not one of their four basic essences, but light was given entirely separate status. They called an atom of light a photon. Today, many types of electromagnetic energy in addition to visible light are recognized, but the term photon is still used.
A photon is the smallest quantity of any type of electromagnetic energy, just as an atom is the smallest quantity of an element. A photon may be pictured as a small bundle of energy, sometimes called a quantum, that travels through space at the speed of light. We speak of x-ray photons, light photons, and other types of electromagnetic energy as photon radiation.
The physics of visible light has always been a subject of investigation apart from other areas of science. Nearly all of the classical laws of optics were described hundreds of years ago. Late in the 19th century, James Clerk Maxwell showed that visible light has both electric and magnetic properties, hence the term electromagnetic energy.
By the beginning of the 20th century, other types of electromagnetic energy had been described, and a uniform theory evolved. Electromagnetic energy is best explained by reference to a model, in much the same way that the atom is best described by the Bohr model.
Velocity and Amplitude
Photons are energy disturbances that move through space at the speed of light (c). Some sources give the speed of light as 186,000 miles per second, but in the SI system of units, it is 3 × 108 m/s.
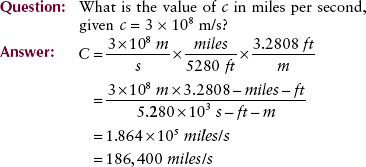
Although photons have no mass and therefore no identifiable form, they do have electric and magnetic fields that are continuously changing in a sinusoidal fashion. Physicists use the term field to describe interactions among different energies, forces, or masses that can otherwise be described only mathematically. For instance, we can understand the gravitational field even though we cannot see it. We know the gravitational field exists because we are held to the Earth by it.
The gravitational field governs the interaction of different masses. Similarly, the electric field governs the interaction of electrostatic charges, and the magnetic field, the interaction of magnetic poles.
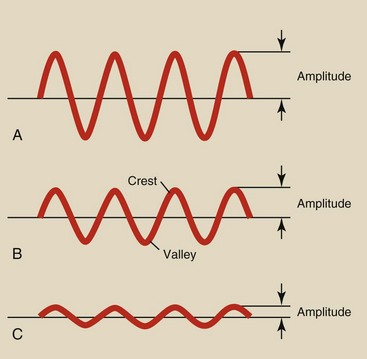
Figure 3-1 shows three examples of a sinusoidal variation. This type of variation is usually called a sine wave. Sine waves can be described by a mathematical formula and therefore have many applications in physics.
Sine waves exist in nature and are associated with many familiar objects (Figure 3-2). Simplistically, sine waves are variations of amplitude over time.
FIGURE 3-2 Sine waves are associated with many naturally occurring phenomena in addition to electromagnetic energy.
Alternating electric current consists of electrons moving back and forth sinusoidally through a conductor. A long rope fastened at one end vibrates as a sine wave if the free end is moved up and down in whiplike fashion.
The arms of a tuning fork vibrate sinusoidally after being struck with a hard object. The weight on the end of a coil spring varies sinusoidally up and down after the spring has been stretched.
The sine waves in Figure 3-1 are identical except for their amplitude; sine wave A has the largest amplitude, and sine wave C has the smallest. Sine wave amplitude is discussed later in connection with high-voltage generation and rectification in an x-ray imaging system.
Frequency and Wavelength
The sine wave model of electromagnetic energy describes variations in the electric and magnetic fields as the photon travels with velocity c. The important properties of this model are frequency, represented by f, and wavelength, represented by the Greek letter lambda (λ).
Another interpretation of the vibrating rope in Figure 3-2 is the Texas roadside critter observing the motion of the rope from a point midway between the fastened end and the scientist (Figure 3-3).
FIGURE 3-3 Moving one end of a rope in a whiplike fashion will set into motion sine waves that travel down the rope to the fastened end. An observer, midway, can determine the frequency of oscillation by counting the crests or valleys that pass a point (A) per unit time.
What does the critter see? If he moves his field of view along the rope, he will observe the crest of the sine wave traveling along the rope to the end. If he fixes his attention on one segment of the rope such as point A, he will see the rope rise and fall harmonically as the waves pass. The more rapidly the scientist holding the loose end moves the rope up and down, the faster the sequence of the rise and fall.
The rate of rise and fall is frequency. It is usually identified as cycles per second. The unit of measurement is the hertz (Hz). One hertz is equal to 1 cycle per second. The frequency is equal to the number of crests or the number of valleys that pass the point of an observer per unit of time. If the critter used a stopwatch and counted 20 crests passing in 10 s, then the frequency would be 20 cycles in 10 s, or 2 Hz. If the scientist doubles the rate at which he moves the rope up and down, the critter would count 40 crests passing in 10 s, and the frequency would be 4 Hz.
The wavelength is the distance from one crest to another, from one valley to another, or from any point on the sine wave to the next corresponding point. Figure 3-4 shows sine waves of three different wavelengths. With a meter rule, you can verify that wave A repeats every 1 cm and therefore has a wavelength of 1 cm. Similarly, wave B has a wavelength of 0.5 cm, and wave C has a wavelength of 1.5 mm. Clearly, then, as the frequency is increased, the wavelength is reduced. The wave amplitude is not related to wavelength or frequency.
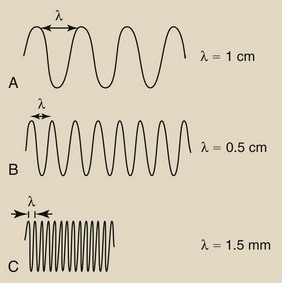
FIGURE 3-4 These three sine waves have different wavelengths. The shorter the wavelength (λ), the higher is the frequency.
Three wave parameters—velocity, frequency, and wavelength—are needed to describe electromagnetic energy. The relationship among these parameters is important. A change in one affects the value of the others. Velocity is constant.
Suppose a radiologic technologist is positioned to observe the flight of the sine wave arrows to determine their frequency (Figure 3-5). The first sine wave is measured and is found to have a frequency of 60 Hz, which signifies 60 oscillations (wavelengths) of the sine wave every second.
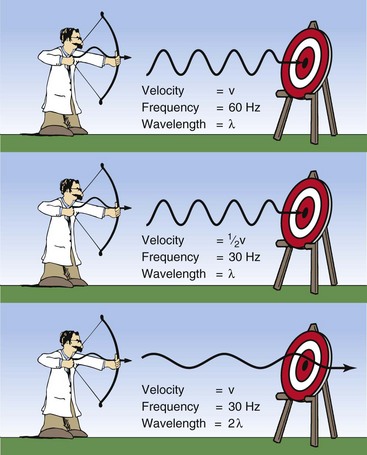
FIGURE 3-5 Relationships among velocity (v), frequency (f), and wavelength (lambda) for any sine wave.
The unknown archer now puts an identical sine wave arrow into his bow and shoots it with less force so that this second arrow has only half the velocity of the first arrow. The observer correctly measures the frequency at 30 Hz even though the wavelength of the second arrow was the same as that of the first arrow. In other words, as the velocity decreases, the frequency decreases proportionately.
Now the archer shoots a third sine wave arrow with precisely the same velocity as the first but with a wavelength twice as long as that of the first. What should be the observed frequency? The correct answer is 30 Hz.
This brief analogy demonstrates how the three parameters associated with a sine wave are interrelated. A simple mathematical formula, called the wave equation, expresses this interrelationship:
The wave equation is used for both sound and electromagnetic energy. However, keep in mind that sound waves are very different from electromagnetic photons. The sources of sound are different, they are propagated in different ways, and their velocities vary greatly. The velocity of sound depends on the density of the material through which it passes. Sound cannot travel through a vacuum.
When dealing with electromagnetic energy, we can simplify the wave equation because all such energy travels with the same velocity.
The product of frequency and wavelength always equals the velocity of light for electromagnetic energy. Stated differently, for electromagnetic energy, frequency and wavelength are inversely proportional. The following are alternative forms of the electromagnetic wave equation.
As the frequency of electromagnetic energy increases, the wavelength decreases and vice versa.
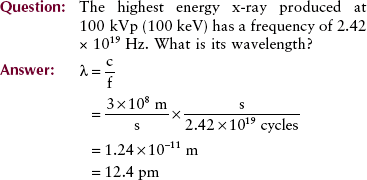
Electromagnetic Spectrum
The frequency range of electromagnetic energy extends from approximately 102 to 1024 Hz. The photon wavelengths associated with these radiations are approximately 107 to 10−16 m, respectively. This wide range of values covers many types of electromagnetic energy, most of which are familiar to us. Grouped together, these types of energy make up the electromagnetic spectrum.
The known electromagnetic spectrum has three regions most important to radiologic science: visible light, x- and gamma radiation, and RF. Other portions of the spectrum include ultraviolet light, infrared light, and microwave radiation.
With all of these various types of energy, photons are essentially the same. Each can be represented as a bundle of energy consisting of varying electric and magnetic fields that travel at the speed of light. The photons of these various portions of the electromagnetic spectrum differ only in frequency and wavelength.
Ultrasound is not produced in photon form and does not have a constant velocity. Ultrasound is a wave of moving molecules. Ultrasound requires matter; electromagnetic energy can exist in a vacuum.
Measurement of the Electromagnetic Spectrum
The electromagnetic spectrum shown in Figure 3-6 contains three different scales, one each for energy, frequency, and wavelength. Because the velocity of all electromagnetic energy is constant, the wavelength and frequency are inversely related.
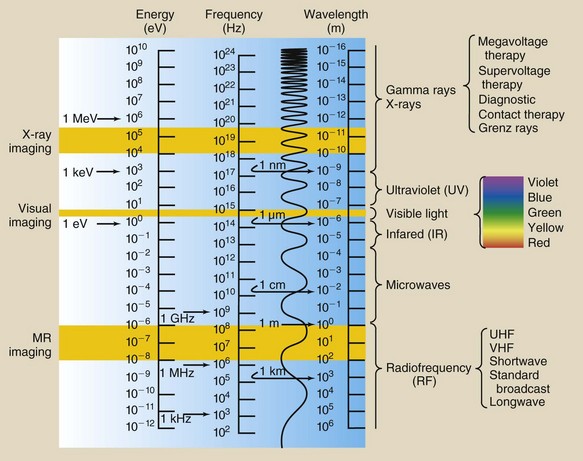
FIGURE 3-6 The electromagnetic spectrum extends over more than 25 orders of magnitude. This chart shows the values of energy, frequency, and wavelength and identifies the three imaging windows.
Although segments of the electromagnetic spectrum are often given precise ranges, these ranges actually overlap because of production methods and detection techniques. For example, by definition, ultraviolet light has a shorter wavelength than violet light and cannot be sensed by the eye. What is visible violet light to one observer, however, may be ultraviolet light to another. Similarly, microwaves and infrared light are indistinguishable in their common region of the spectrum.
The earliest investigations focused on visible light. Studies of reflection, refraction, and diffraction showed light to be wavelike. Consequently, visible light is described by wavelength, measured in nanometers (nm).
In the 1880s, some scientists began to experiment with the radio, which required the oscillation of electrons in a conductor. Consequently, the unit of frequency, the hertz, is used to describe radio waves.
Finally, in 1895, Roentgen discovered x-rays by applying an electric potential (kilovolts) across a Crookes tube. Consequently, x-rays are described in terms of a unit of energy, the electron volt (eV).
It should be clear that these three scales are directly related mathematically. If you know the value of electromagnetic energy on one scale, you can easily compute its value on the other two.
The electromagnetic spectrum has been scientifically investigated for longer than a century. Scientists working with energy in one portion of the spectrum were often unaware of others investigating another portion. Consequently, there is no generally accepted, single dimension for measuring electromagnetic energy.
Visible Light
An optical physicist describes visible light in terms of wavelength. When sunlight passes through a prism (Figure 3-7), it emerges not as white sunlight but as the colors of the rainbow.
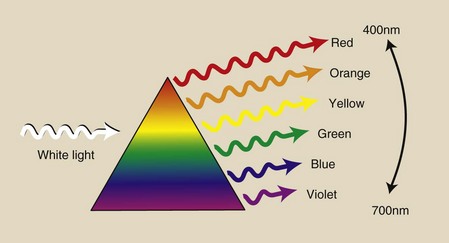
FIGURE 3-7 When it passes through a prism, white light is refracted into its component colors. These colors have wavelengths that extend from approximately 400 to 700 nm.
Although photons of visible light travel in straight lines, their course can be deviated when they pass from one transparent medium to another. This deviation in line of travel, called refraction, is the cause of many peculiar but familiar phenomena, such as a rainbow or the apparent bending of a straw in a glass of water.
White light is composed of photons of a range of wavelengths, and the prism acts to separate and group the emerging light into colors because different wavelengths are refracted through different angles. The component colors of white light have wavelength values ranging from approximately 400 nm for violet to 700 nm for red.
Visible light occupies the smallest segment of the electromagnetic spectrum, and yet it is the only portion that we can sense directly. Sunlight also contains two types of invisible light: infrared and ultraviolet.
Infrared light consists of photons with wavelengths longer than those of visible light but shorter than those of microwaves. Infrared light heats any substance on which it shines. It may be considered radiant heat.
Ultraviolet light is located in the electromagnetic spectrum between visible light and ionizing radiation. It is responsible for molecular interactions that can result in sunburn.
Radiofrequency
A radio or television engineer describes radio waves in terms of their frequency. For example, radio station WIMP might broadcast at 960 kHz, and its associated television station WIMP-TV might broadcast at 63.7 MHz. Communication broadcasts are usually identified by their frequency of transmission and are called radiofrequency (RF) emissions.
Radiofrequency covers a considerable portion of the electromagnetic spectrum. RF has relatively low energy and relatively long wavelength. Ham operators speak of broadcasting on the 10-m band or the 30-m band; these numbers refer to the approximate wavelength of emission.
Standard AM radio broadcasts have a wavelength of about 100 m. Television and FM broadcasting occur at much shorter wavelengths. Because microwaves are also used for communication, RF and microwave emissions overlap considerably.
Very-short-wavelength RF is microwave radiation. Microwave frequencies vary according to use but are always higher than broadcast RF and lower than infrared. Microwaves have many uses, such as cellular telephone communication, highway speed monitoring, medical diathermy, and hotdog preparation.
Ionizing Radiation
Different from RF or visible light, ionizing electromagnetic energy usually is characterized by the energy contained in a photon. When an x-ray imaging system is operated at 80 kVp, the x-rays it produces contain energies ranging from 0 to 80 keV.
An x-ray photon contains considerably more energy than a visible light photon or an RF photon. The frequency of x-radiation is much higher and the wavelength much shorter than for other types of electromagnetic energy.
It is sometimes said that gamma rays have higher energy than x-rays. In the early days of radiology, this was true because of the limited capacity of available x-ray imaging systems. Today, linear accelerators make it possible to produce x-rays of considerably higher energies than gamma ray emissions. Consequently, the distinction by energy is not appropriate.
X-rays are emitted from the electron cloud of an atom that has been stimulated artificially (Figure 3-8). Gamma rays, on the other hand, come from inside the nucleus of a radioactive atom (Figure 3-9).
Whereas x-rays are produced in diagnostic imaging systems, gamma rays are emitted spontaneously from radioactive material. Nevertheless, given an x-ray and a gamma ray of equal energy, one could not tell them apart.
This situation is analogous to the difference between beta particles and electrons. These particles are the same except that beta particles come from the nucleus and electrons come from outside the nucleus.
Visible light is identified by wavelength, radiofrequency is identified by frequency, and x-rays are identified by energy.
Again, three regions of the electromagnetic spectrum are particularly important to radiologic science. Naturally, the x-ray region is fundamental to producing a high-quality radiograph. The visible light region is also important because the viewing conditions of a radiographic or fluoroscopic image are critical to diagnosis. With the introduction of magnetic resonance imaging (MRI), the RF region has become more important in medical imaging.
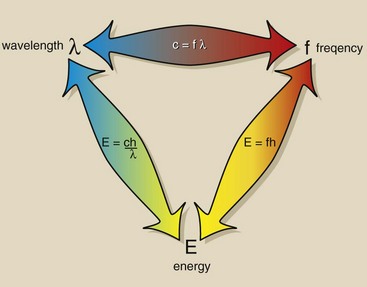
The electromagnetic relationship triangle (Figure 3-10) can be helpful in relating each scale to the other two.
Wave-Particle Duality
A photon of x-radiation and a photon of visible light are fundamentally the same except that x-radiation has much higher frequency, and hence a shorter wavelength, than visible light. These differences result in differences in the way these photons interact with matter.
Visible-light photons tend to behave more like waves than particles. The opposite is true of x-ray photons, which behave more like particles than waves. In fact, both types of photons exhibit both types of behavior— a phenomenon known as the wave-particle duality of electromagnetic energy.
Photons interact with matter most easily when the matter is approximately the same size as the photon wavelength.
Another general way to consider the interaction of electromagnetic radiation with matter is as a function of wavelength. Radio and TV waves, whose wavelengths are measured in meters, interact with metal rods or wires called antennas.
Microwaves, whose wavelengths are measured in centimeters, interact most easily with objects of the same size, such as hotdogs and hamburgers.
The wavelength of visible light is measured in nanometers (nm); visible light interacts with living cells, such as the rods and cones of the eye. Ultraviolet light interacts with molecules, and x-rays interact with electrons and atoms. All radiation with wavelength longer than those of x-radiation interacts primarily as a wave phenomenon.
Wave Model: Visible Light
One of the unique features of animal life is the sense of vision. It is interesting that we have developed organs that sense only a very narrow portion of the enormous spread of the electromagnetic spectrum. This narrow portion is called visible light.
The visible-light spectrum extends from short-wavelength violet radiation through green and yellow to long-wavelength red radiation. On either side of the visible-light spectrum are ultraviolet light and infrared light. Neither can be detected by the human eye, but they can be detected by other means, such as a photographic emulsion.
Visible light interacts with matter very differently from x-rays. When a photon of light strikes an object, it sets the object’s molecules into vibration. The orbital electrons of some atoms of certain molecules are excited to an energy level that is higher than normal. This energy is immediately re-emitted as another photon of light; it is reflected.
The atomic and molecular structures of any object determine which wavelengths of light are reflected. A leaf in the sunlight appears green because nearly all of the visible-light photons are absorbed by the leaf. Only photons with wavelengths in the green region are reflected. Similarly, a balloon may appear red by absorbing all visible light photons except long-wavelength red photons, which are reflected.
Many familiar phenomena of light, such as reflection, absorption, and transmission, are most easily explained by using the wave model of electromagnetic energy. When a pebble is dropped into a still pond, ripples radiate from the center of the disturbance like miniature waves.
This situation is similar to the wave nature of visible light. Figure 3-11 shows the difference in the water waves between an initial disturbance caused by a small object and one caused by a large object. The distance between the crests of waves is much greater with the large object than with the small object.
FIGURE 3-11 A small object dropped into a smooth pond creates waves of short wavelength. A large object creates waves of much longer wavelength.
With these water waves, the difference in wavelength is proportional to the energy introduced into the system. With light, the opposite is true: The shorter the photon wavelength, the higher is the photon energy.
If the analogy of the pebble in the pond is extended to a continuous succession of pebbles dropped into a smooth ocean, then at the edge of the ocean, the waves will appear straight rather than circular. Light waves behave as though they were straight rather than circular because the distance from the source is so great. The manner in which light is reflected from or transmitted through a surface is a consequence of this straight wavelike motion.
When the waves of the ocean crash into a vertical bulkhead (Figure 3-12), the reflected waves scatter from the bulkhead at the same angle at which the incident waves struck it. When the bulkhead is removed and replaced with a beach, the water waves simply crash onto the beach, dissipate their energy, and are absorbed. When an intermediate condition exists in which the bulkhead has been replaced by a line of pilings, the energy of the waves is scattered and absorbed.
FIGURE 3-12 Energy is reflected when waves crash into a bulkhead. It is absorbed by a beach. It is partially absorbed or attenuated by a line of pilings. Light is also reflected, absorbed, or attenuated, depending on the composition of the surface on which it is incident.
Electromagnetic energy attenuation is the reduction in intensity that results from scattering and absorption.
Visible light can similarly interact with matter. Reflection from the silvered surface of a mirror is common. Examples of transmission, absorption, and attenuation of light are equally easy to identify. When light waves are absorbed, the energy deposited in the absorber reappears as heat. A black asphalt road reflects very little visible light but absorbs a considerable amount. In so doing, the road surface can become quite hot.
Just a slight modification can change how some materials transmit or absorb light. There are three degrees of interaction between light and an absorbing material: transparency, translucency, and opacity (Figure 3-13).
FIGURE 3-13 Objects absorb light in three degrees: not at all (transmission), partially (attenuation), and completely (absorption). The objects associated with these degrees of absorption are called transparent, translucent, and opaque, respectively.
Window glass is transparent; it allows light to be transmitted almost unaltered. One can see through glass because the surface is smooth and the molecular structure is tight and orderly. Incident light waves cause molecular and electronic vibrations within the glass. These vibrations are transmitted through the glass and are re-irradiated almost without change.
When the surface of the glass is roughened with sandpaper, light is still transmitted through the glass but is greatly scattered and reduced in intensity. Instead of seeing clearly, one sees only blurred forms. Such glass is translucent.
When the glass is painted black, the characteristics of the pigment in the paint are such that no light can pass through. Any incident light is totally absorbed in the paint. Such glass is opaque to visible light.
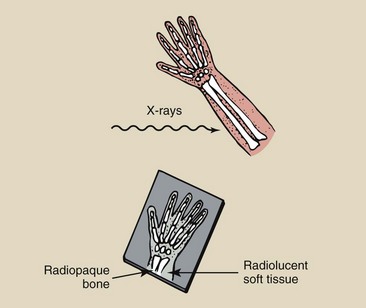
The terms radiopaque and radiolucent are used routinely in x-ray diagnosis to describe the visual appearance of anatomical structures. Structures that absorb x-rays are called radiopaque. Structures that transmit x-rays are called radiolucent (Figure 3-14). Whereas bone is radiopaque, lung tissue and to some extent soft tissue are radiolucent.
Inverse Square Law
When light is emitted from a source such as the sun or a light bulb, the intensity decreases rapidly with the distance from the source. X-rays exhibit precisely the same property. Figure 3-15 shows that as a book is moved farther from a light source, the intensity of light falls.
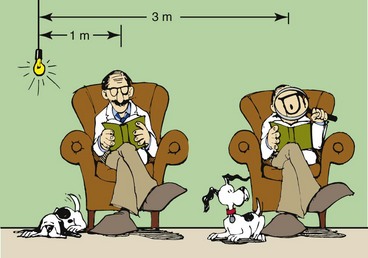
FIGURE 3-15 The inverse square law describes the relationship between radiation intensity and distance from the radiation source.
This decrease in intensity is inversely proportional to the square of the distance of the object from the source. Mathematically, this is called the inverse square law and is expressed as follows:
Inverse Square Law
where I1 is the intensity at distance d1 from the source and I2 is the intensity at distance d2 from the source.
The reason for the rapid decrease in intensity with increasing distance is that the total light emitted is spread out over an increasingly larger area. The equivalent of this phenomenon in the water wave analogy is the reduction of wave amplitude with distance from the source. The wavelength remains fixed.
Electromagnetic energy (radiation) intensity is inversely related to the square of the distance from the source.
If the source of electromagnetic energy is not a point but rather a line, such as a fluorescent lamp, the inverse square law does not hold at distances close to the source. At great distances from the source, the inverse square law can be applied.
The inverse square law can be applied to distances greater than seven times the longest dimension of the source.
To apply the inverse square law, you must know three of the four parameters, which consist of two distances and two intensities. The usual situation involves a known intensity at a given distance from the source and an unknown intensity at a greater distance.
This relationship between electromagnetic energy (radiation) intensity and distance from the source applies equally well to x-ray intensity.
This example illustrates that when the distance from the source is doubled, the intensity of radiation is reduced to one fourth; conversely, when the distance is halved, the intensity is increased by a factor of four.
Often it is necessary to determine the distance from the source at which the radiation has a given intensity. This type of problem is commonly encountered in designing radiologic facilities.
In the previous exercises, the intensity of the x-ray beam is calculated at a distance that assumes that the source is constant. In practical radiography, it is usual to work the other way around. One must calculate what the intensity of the beam should be at the source (i.e., the x-ray focal spot), so that exposure at the distance to the image receptor will remain constant. Thus, later, we will use the above formula but with one side inverted and will call it The Square Law.
Particle Model: Quantum Theory
In contrast to other portions of the electromagnetic spectrum, x-rays are usually identified by their energy, measured in electron volts (eV). X-ray energy ranges from approximately 10 keV to 50 MeV. The associated wavelength for this range of x-radiation is approximately 10−10 to 10−14 m. The frequency of these photons ranges from approximately 1018 to 1022 Hz.
Table 3-1 describes the various types of x-rays produced and the general use that is made of each. We are interested primarily in the diagnostic range of x-radiation, although what is said for that range holds equally well for other types of x-radiation.
TABLE 3-1
Examples of the Wide Range of X-rays Produced by Application in Medicine, Research, and Industry
| Type of X-Ray | Approximate kVp | Application |
| Diffraction | <10 | Research: structural and molecular analysis |
| Grenz rays* | 10–20 | Medicine: dermatology |
| Superficial | 50–100 | Medicine: therapy of superficial tissues |
| Diagnostic | 30–150 | Medicine: imaging anatomical structures and tissues |
| Orthovoltage* | 200–300 | Medicine: therapy of deep-lying tissues |
| Supervoltage* | 300–1000 | Medicine: therapy of deep-lying tissues |
| Megavoltage | >1000 (1MV) | Medicine: therapy of deep-lying tissues |
| Industry: checking integrity of welded metals |
An x-ray photon can be thought of as containing an electric field and a magnetic field that vary sinusoidally at right angles to each other with a beginning and an end that have diminishing amplitude (Figure 3-16). The wavelength of an x-ray photon is measured similarly to that of any electromagnetic energy: It is the distance from any position on the sine wave to the corresponding position of the next wave. The frequency of an x-ray photon is calculated similarly to the frequency of any electromagnetic photon, with use of the wave equation.
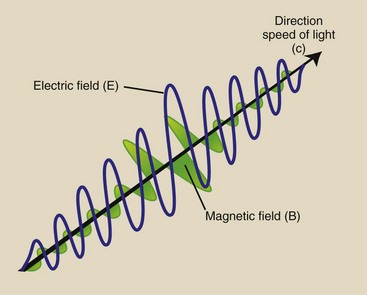
FIGURE 3-16 All electromagnetic radiation, including x-rays, can be visualized as two perpendicular sine waves that travel in a straight line at the speed of light. One of the sine waves represents an electric field and the other a magnetic field.
X-rays are created with the speed of light (c), and they exist with velocity (c) or they do not exist at all. That is one of the substantive statements of Planck’s quantum theory. Max Planck was a German physicist whose mathematical and physical theories synthesized our understanding of electromagnetic radiation into a uniform model; for this work, he received the Nobel Prize in 1918.
Another important consequence of this theory is the relationship between energy and frequency: Photon energy is directly proportional to photon frequency. The constant of proportionality, known as Planck’s constant and symbolized by h, has a numeric value of 4.15 × 10−15 eVs or 6.63 × 10−34 Js. Mathematically, the relationship between energy and frequency is expressed as follows:
Planck’s Quantum Equation
where E is the photon energy, h is Planck’s constant, and f is the photon frequency in hertz.
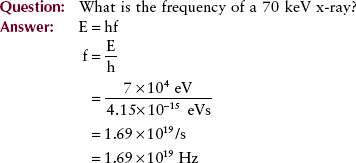
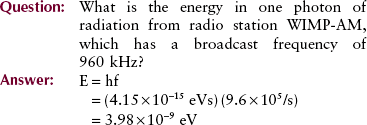
An extension of Planck’s equation is the relationship between photon energy and photon wavelength; this relationship is useful in computing equivalent wavelengths of x-rays and other types of radiation.
In other words, photon energy is inversely proportional to photon wavelength. In this relationship, the constant of proportionality is a combination of two constants, Planck’s constant and the speed of light. The longer the wavelength of electromagnetic energy, the lower is the energy of each photon.
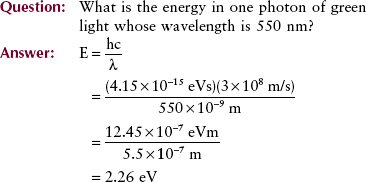
Matter and Energy
We began Chapter 1 with the statement that everything in existence can be classified as matter or energy. We further stated that matter and energy are really manifestations of each other. According to classical physics, matter can be neither created nor destroyed, a law known as the law of conservation of matter. A similar law, the law of conservation of energy, states that energy can be neither created nor destroyed.
Einstein and Planck greatly extended these theories. According to quantum physics and the physics of relativity, matter can be transformed into energy and vice versa. Nuclear fission, the basis for generating electricity, is an example of converting matter into energy. In radiology, a process known as pair production (see Chapter 9) is an example of the conversion of energy into mass.
A simple relationship introduced in Chapter 1 allows the calculation of energy equivalence of mass and mass equivalence of energy. This equation is a consequence of Einstein’s theory of relativity and is familiar to all.
Similar to the electron volt, the joule (J) is a unit of energy. One joule is equal to 6.24 × 1018 eV.
Relativity
E in the equation is the energy measured in joules, m is the mass measured in kilograms, and c is the velocity of light measured in meters per second.
The problem might be stated in the opposite direction as follows.
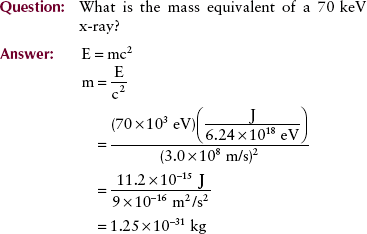
By using the relationships reported earlier, one can calculate the mass equivalence of a photon when only the photon wavelength or photon frequency is known.
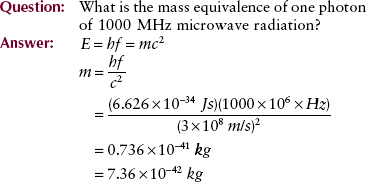
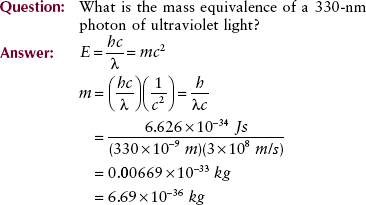
Calculations of this type can be used to set up a scale of mass equivalence for the electromagnetic spectrum (Figure 3-17). This scale can be used to check the answers to the previous examples and to some of the problems in the companion Workbook and Laboratory Manual.
Summary
Although matter and energy are interchangeable, x-ray imaging is based on energy in the form of x-ray photons that interact with tissue and an image receptor.
X-rays are one type of photon of electromagnetic energy. Frequency, wavelength, velocity, and amplitude are used to describe the various imaging regions of the electromagnetic spectrum. These characteristics of electromagnetic energy determine how such radiation interacts with matter.
1. Define or otherwise identify the following:
2. Accurately diagram one photon of orange light (λ = 620 nm) and identify its velocity, electric field, magnetic field, and wavelength.
3. A thunderclap associated with lightning has a frequency of 800 Hz. If its wavelength is 50 cm, what is its velocity? How far away is the thunder if the time interval between seeing the lightning and hearing the thunder is 6 s?
4. What is the frequency associated with a photon of microwave radiation that has a wavelength of 10−4 m?
5. Radio station WIMP-FM broadcasts at 104 MHz. What is the wavelength of this radiation?
6. In mammography, 26 keV x-rays are used. What is the frequency of this radiation?
7. Radiography of a barium-filled colon calls for high-kVp technique. These x-rays can have energy of 110 keV. What is the frequency and wavelength of this radiation?
8. What is the energy of the 110 keV x-ray in question 7 when expressed in joules? What is its mass equivalence?
9. The output intensity of a normal radiographic imaging system is 0.05 mGya/mAs at 100 cm. What is the output intensity of such a system at 200 cm?
10. A mobile x-ray imaging system has an output intensity of 0.04 mGya at 100 cm. Conditions require that a particular examination be conducted at 75 cm SID. What will be the output intensity at this distance?
12. How are frequency and wavelength related?
13. Write the inverse square law and describe its meaning.
14. The intensity of light from a reading lamp is 200 millilumens (mlm) at a distance of 2 meters (m). What is the intensity of light at 3 m?
15. What are the three imaging windows of the electromagnetic spectrum, and what unit of measure is applied to each?
16. What is the energy range of diagnostic x-rays?
17. What is the difference between x-rays and gamma rays?
18. Some regions of the electromagnetic spectrum behave like waves, and some regions behave like particles in their interaction with matter. What is this phenomenon called?
The answers to the Challenge Questions can be found by logging on to our website at http://evolve.elsevier.com.