X-ray Interaction with Matter
At the completion of this chapter, the student should be able to do the following:
1 Describe each of the five x-ray interactions with matter.
2 Define differential absorption and describe its effect on image contrast.
3 Explain the effect of atomic number and mass density of tissue on differential absorption.
4 Discuss why radiologic contrast agents are used to image some tissues and organs.
5 Explain the difference between absorption and attenuation.
X-RAYS INTERACT with matter in the following five ways: (1) coherent scattering, (2) Compton scattering, (3) photoelectric effect, (4) pair production, and (5) photodisintegration. Only Compton scattering and photoelectric effect are important in making an x-ray image. The conditions that govern these two interactions control differential absorption, which determines the degree of contrast of an x-ray image.
Five X-Ray Interactions with Matter
In Chapter 3, the interaction between electromagnetic radiation and matter was described briefly. This interaction was said to have wavelike and particle-like properties. Electromagnetic radiation interacts with structures that are similar in size to the wavelength of the radiation.
X-rays have very short wavelengths, approximately 10−8 to 10−9 m. The higher the energy of an x-ray, the shorter is its wavelength. Consequently, low-energy x-rays tend to interact with whole atoms, which have diameters of approximately 10−9 to 10−10 m; moderate-energy x-rays generally interact with electrons, and high-energy x-rays generally interact with nuclei.
X-rays interact at these various structural levels through five mechanisms: coherent scattering, Compton scattering, photoelectric effect, pair production, and photodisintegration. Two of these—Compton scattering and photoelectric effect—are of particular importance to diagnostic radiology. They are discussed in some detail here.
Coherent Scattering
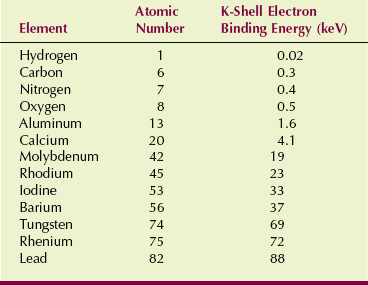
X-rays with energies below approximately 10 keV interact with matter by coherent scattering, sometimes called classical scattering or Thompson scattering (Figure 9-1). J.J. Thompson was the physicist to first describe coherent scattering.
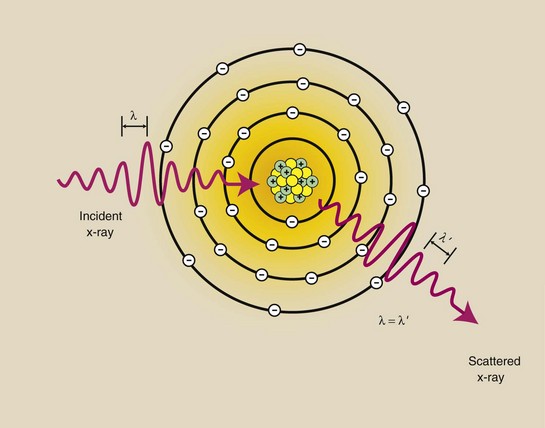
FIGURE 9-1 Coherent scattering is an interaction between low-energy x-rays and atoms. The x-ray loses no energy but changes direction slightly. The wavelength of the incident x-ray is equal to the wavelength of the scattered x-ray.
In coherent scattering, the incident x-ray interacts with a target atom, causing it to become excited. The target atom immediately releases this excess energy as a scattered x-ray with wavelength equal to that of the incident x-ray (λ = λ′) and therefore of equal energy. However, the direction of the scattered x-ray is different from that of the incident x-ray.
The result of coherent scattering is a change in direction of the x-ray without a change in its energy. There is no energy transfer and therefore no ionization. Most coherently scattered x-rays are scattered in the forward direction.
Coherent scattering primarily involves low-energy x-rays, which contribute little to the medical image. Some coherent scattering, however, occurs throughout the diagnostic range. At 70 kVp, a few percent of the x-rays undergo coherent scattering, which contributes slightly to image noise, the general graying of an image that reduces image contrast.
Compton Scattering
X-rays throughout the diagnostic range can undergo an interaction with outer-shell electrons that not only scatters the x-ray but reduces its energy and ionizes the atom as well. This interaction is called Compton scattering (Figure 9-2).
FIGURE 9-2 Compton scattering occurs between moderate-energy x-rays and outer-shell electrons. It results in ionization of the target atom, a change in x-ray direction, and a reduction in x-ray energy. The wavelength of the scattered x-ray is greater than that of the incident x-ray.
In Compton scattering, the incident x-ray interacts with an outer-shell electron and ejects it from the atom, thereby ionizing the atom. The ejected electron is called a Compton electron. The x-ray continues in a different direction with less energy.
The energy of the Compton-scattered x-ray is equal to the difference between the energy of the incident x-ray and the energy of the ejected electron. The energy of the ejected electron is equal to its binding energy plus the kinetic energy with which it leaves the atom. Mathematically, this energy transfer is represented as follows:
Compton Effect
where Ei is energy of the incident x-ray, Es is energy of the scattered x-ray, Eb is electron binding energy, and EKE is kinetic energy of the electron.
During Compton scattering, most of the energy is divided between the scattered x-ray and the Compton electron. Usually, the scattered x-ray retains most of the energy. Both the scattered x-ray and the Compton electron may have sufficient energy to undergo additional ionizing interactions before they lose all their energy.
Ultimately, the scattered x-ray is absorbed photoelectrically. The Compton electron loses all of its kinetic energy through ionization and excitation and drops into a vacancy in an electron shell previously created by some other ionizing event.
Compton-scattered x-rays can be deflected in any direction, including 180 degrees from the incident x-ray. At a deflection of 0 degrees, no energy is transferred. As the angle of deflection increases to 180 degrees, more energy is transferred to the Compton electron, but even at 180 degrees of deflection, the scattered x-ray retains at least approximately two thirds of its original energy.
X-rays scattered back in the direction of the incident x-ray beam are called backscatter radiation. In radiography, backscatter radiation is responsible for the cassette-hinge image sometimes seen on a radiograph even though the hinge was on the back side of the cassette. In such situations, the x-radiation has backscattered from the wall or the examination table, not from the patient.
The probability that a given x-ray will undergo Compton scattering is a complex function of the energy of the incident x-ray. In general, the probability of Compton scattering decreases as x-ray energy increases.
The probability of Compton scattering is inversely proportional to x-ray energy (1/E) and independent of atomic number.
The probability of Compton scattering does not depend on the atomic number of the atom involved. Any given x-ray is just as likely to undergo Compton scattering with an atom of soft tissue as with an atom of bone (Figure 9-3). Table 9-1 summarizes Compton scattering.
TABLE 9-1
Features of Compton Scattering
| Most Likely to Occur | With Outer-Shell Electrons |
| With loosely bound electrons | |
| As x-ray energy increases | Increased penetration through tissue without interaction |
| Increased Compton scattering relative to photoelectric effect | |
| Reduced Compton scattering (≈1/E) | |
| As atomic number of absorber increases | No effect on Compton scattering |
| As mass density of absorber increases | Proportional increase in Compton scattering |
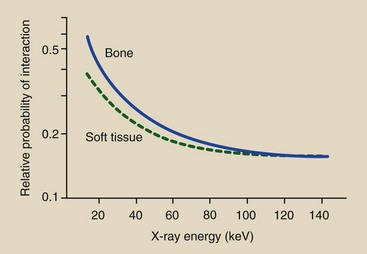
FIGURE 9-3 The probability that an x-ray will interact through Compton scattering is about the same for atoms of soft tissue and those of bone. This probability decreases with increasing x-ray energy.
Compton scattering in tissue can occur with all x-rays and therefore is of considerable importance in x-ray imaging. However, its importance involves a negative sense. Scattered x-rays provide no useful information on the radiograph. Rather, they produce a uniform optical density on the screen-film radiograph and uniform intensity on the digital image receptor that results in reduced image contrast. Ways of reducing this scattered radiation are discussed later, but none is totally effective.
The scattered x-rays from Compton scatterings can create a serious radiation exposure hazard in radiography and particularly in fluoroscopy. A large amount of radiation can be scattered from the patient during fluoroscopy. Such radiation is the source of most of the occupational radiation exposure that radiographers receive.
During radiography, the hazard is less severe because no one but the patient is usually in the examining room. Nevertheless, scattered radiation levels are sufficient to necessitate protective shielding of the x-ray examining room.
Photoelectric Effect
X-rays in the diagnostic range also undergo ionizing interactions with inner-shell electrons. The x-ray is not scattered, but it is totally absorbed. This process is called the photoelectric effect (Figure 9-4) and earned Albert Einstein the 1921 Nobel Prize in physics.
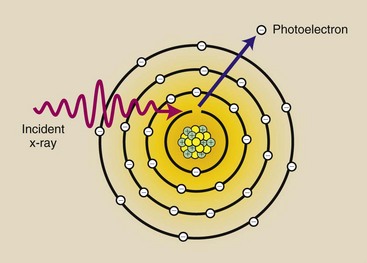
FIGURE 9-4 The photoelectric effect occurs when an incident x-ray is totally absorbed during the ionization of an inner-shell electron. The incident photon disappears, and the K-shell electron, now called a photoelectron, is ejected from the atom.
The electron removed from the atom, called a photoelectron, escapes with kinetic energy equal to the difference between the energy of the incident x-ray and the binding energy of the electron. Mathematically, this is shown as follows:
Photoelectric Effect
where Ei is the energy of the incident x-ray, Eb is the electron-binding energy, and EKE is the kinetic energy of the electron.
For low atomic number atoms, such as those found in soft tissue, the binding energy of even K-shell electrons is low (e.g., 0.3 keV for carbon). Therefore, the photoelectron is released with kinetic energy nearly equal to the energy of the incident x-ray.
For higher atomic number target atoms, electron binding energies are higher (37 keV for barium K-shell electrons). Therefore, the kinetic energy of the photoelectron from barium is proportionately lower. Table 9-2 shows the approximate K-shell binding energy for elements of radiologic importance.
Characteristic x-rays are produced after a photoelectric interaction in a manner similar to that described in Chapter 7. Ejection of a K-shell photoelectron by the incident x-ray results in a vacancy in the K shell. This unnatural state is immediately corrected when an outer-shell electron, usually from the L shell, drops into the vacancy.
This electron transition is accompanied by the emission of an x-ray whose energy is equal to the difference between binding energies of the shells involved. These characteristic x-rays consist of secondary radiation and behave in the same manner as scattered radiation. They contribute nothing of diagnostic value and fortunately have sufficiently low energy that they do not penetrate to the image receptor.
The probability that a given x-ray will undergo a photoelectric interaction is a function of both the x-ray energy and the atomic number of the atom with which it interacts.
The probability of the photoelectric effect is inversely proportional to the third power of the x-ray energy (1/E)3.
A photoelectric interaction cannot occur unless the incident x-ray has energy equal to or greater than the electron binding energy. A barium K-shell electron bound to the nucleus by 37 keV cannot be removed by a 36-keV x-ray.
If the incident x-ray has sufficient energy, the probability that it will undergo a photoelectric effect decreases with the third power of the photon energy (1/E)3. This relationship is shown graphically in Figure 9-5 for soft tissue and bone.
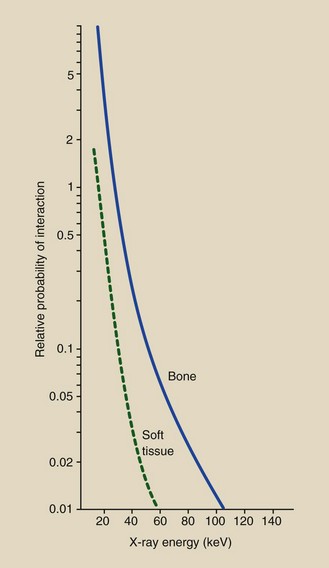
FIGURE 9-5 The relative probability that a given x-ray will undergo a photoelectric interaction is inversely proportional to the third power of the x-ray energy and directly proportional to the third power of the atomic number of the absorber.
The probability of photoelectric effect is directly proportional to the third power of the atomic number of the absorbing material (Z3).
As the relative vertical displacement between the graphs of soft tissue and bone demonstrates, a photoelectric interaction is much more likely to occur with high-Z atoms than with low-Z atoms (see Figure 9-5). Table 9-3 presents the effective atomic numbers of materials of radiologic importance.
Semilogarithmic Graphs
Figure 9-5 is an example of a graph with a logarithmic (log for short) scale along the vertical axis. A log scale is a power of 10 scale used to plot data that cover several orders of magnitude. In Figure 9-5, for example, the relative probability of photoelectric interaction with soft tissue varies from approximately 2 to less than 0.01 over the energy range from 10 to 60 keV.
A plot of these data in conventional arithmetic form appears in Figure 9-6. Clearly, this type of graph is unacceptable because all probability values above 30 keV are so close to zero.
FIGURE 9-6 Relative probability for photoelectric interaction ranges over several orders of magnitude. If it is plotted in the conventional linear fashion, as here, one cannot estimate its value above an energy of approximately 30 keV.
On a linear scale, equal intervals have equal numeric value, but on a log scale, equal intervals represent equal ratios. This difference in scales is shown in Figure 9-7.
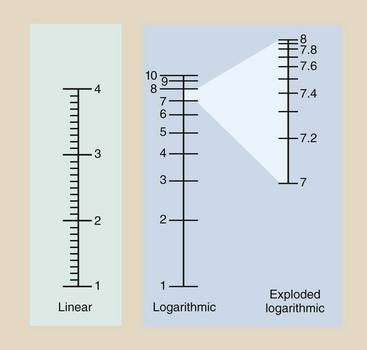
FIGURE 9-7 Graphic scales can be linear or logarithmic. The log scale is used to plot wide ranges of values.
All major intervals on the linear scale have a value of 1, and the subintervals have a value of 0.1. On the other hand, the log scale contains major intervals that each equal one order of magnitude, with subintervals that are not equal in length.
Cubic Relationships
The probability of interaction proportional to the third power changes rapidly. For the photoelectric effect, this means that a small variation in atomic number of the tissue atom or in x-ray energy results in a large change in the chance of photoelectric interaction. This is unlike the situation that exists for Compton scattering.
Table 9-4 summarizes the photoelectric effect.
TABLE 9-4
Features of Photoelectric Effect
| Most likely to occur | With inner-shell electrons |
| With tightly bound electrons | |
| When x-ray energy is just higher than electron binding energy | |
| As x-ray energy increases | Increased penetration through tissue without interaction |
| Less photoelectric effect relative to Compton scattering | |
| Reduced absolute photoelectric effect (≈1/E)3 | |
| As atomic number of absorber increases | Increases proportionately with the cube of the atomic number (Z3) |
| As mass density of absorber increases | Proportional increase in photoelectric absorption |
Pair Production
If an incident x-ray has sufficient energy, it may escape interaction with electrons and come close enough to the nucleus of the atom to be influenced by the strong nuclear field. The interaction between the x-ray and the nuclear field causes the x-ray to disappear, and in its place, two electrons appear, one positively charged (positron) and one negatively charged. This process is called pair production (Figure 9-8).
FIGURE 9-8 Pair production occurs with x-rays that have energies greater than 1.02 MeV. The x-ray interacts with the nuclear field, and two electrons that have opposite electrostatic charges are created.
In Chapter 3, we calculated the energy equivalence of the mass of an electron to be 0.51 MeV. Because two electrons are formed in pair production interaction, the incident x-ray photon must have at least 1.02 MeV of energy.
An x-ray with less than 1.02 MeV cannot undergo pair production. Any of the x-ray’s energy in excess of 1.02 MeV is distributed equally between the two electrons as kinetic energy.
The electron that results from pair production loses energy through excitation and ionization and eventually fills a vacancy in an atomic orbital shell. The positron unites with a free electron, and the mass of both particles is converted to energy in a process called annihilation radiation.
Because pair production involves only x-rays with energies greater than 1.02 MeV, it is unimportant in x-ray imaging, but it is very important for positron emission tomography imaging in nuclear medicine.
Photodisintegration
X-rays with energy above approximately 10 MeV can escape interaction with electrons and the nuclear field and be absorbed directly by the nucleus. When this happens, the nucleus is raised to an excited state and instantly emits a nucleon or other nuclear fragment. This process is called photodisintegration (Figure 9-9).
Differential Absorption
Of the five ways an x-ray can interact with tissue, only two are important to radiology, Compton scattering and the photoelectric effect. Similarly, only two methods of x-ray production (see Chapter 7)—bremsstrahlung x-rays and characteristic x-rays—are important.
More important than interaction of the x-ray by Compton scattering or photoelectric effect, however, is the x-ray transmitted through the body without interacting. Figure 9-10 shows schematically how each of these types of x-ray contributes to an image.
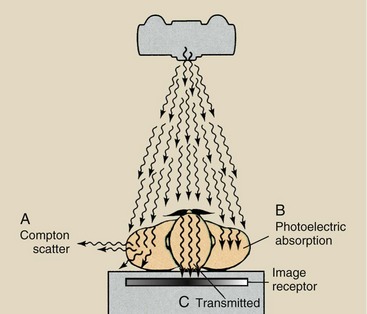
FIGURE 9-10 Three types of x-rays are important to the making of a radiograph: those scattered by Compton interaction (A), those absorbed photoelectrically (B), and those transmitted through the patient without interaction (C).
Differential absorption occurs because of Compton scattering, photoelectric effect, and x-rays transmitted through the patient.
The Compton-scattered x-ray contributes no useful information to the image. When a Compton-scattered x-ray interacts with the image receptor, the image receptor assumes that the x-ray came straight from the x-ray tube target (Figure 9-11). The image receptor does not recognize the scattered x-ray as representing an interaction off the straight line from the target.
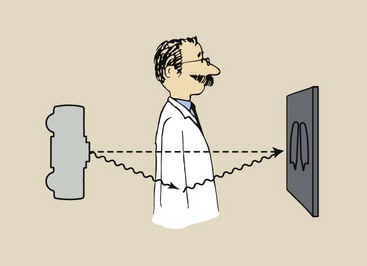
FIGURE 9-11 When an x-ray is Compton scattered, the image receptor thinks it came straight from the source.
These scattered x-rays result in image noise, a generalized dulling of the image by x-rays not representing diagnostic information. To reduce this type of noise, we use techniques and apparatus to reduce the number of scattered x-rays that reach the image receptor.
X-rays that undergo photoelectric interaction provide diagnostic information to the image receptor. Because they do not reach the image receptor, these x-rays are representative of anatomical structures with high x-ray absorption characteristics; such structures are radiopaque. The photoelectric absorption of x-rays produces the light areas in a radiograph, such as those corresponding to bone.
Other x-rays penetrate the body and are transmitted to the image receptor with no interaction whatsoever. They produce the dark areas of a radiograph. The anatomical structures through which these x-rays pass are radiolucent.
Basically, an x-ray image results from the difference between those x-rays absorbed photoelectrically in the patient and those transmitted to the image receptor. This difference in x-ray interaction is called differential absorption.
Approximately 1% of the x-rays incident on a patient reach the image receptor. Fewer than half of those that reach the image receptor interact to form an image. Thus, the radiographic image results from approximately 0.5% of the x-rays emitted by the x-ray tube. Consequently, careful control and selection of the x-ray beam are necessary to produce high-quality radiographs.
Producing a high-quality radiograph requires the proper selection of kVp, so that the effective x-ray energy results in maximum differential absorption. Unfortunately, reducing the kVp to increase differential absorption and therefore image contrast results in increased patient dose. A compromise is necessary for each examination.
Dependence on Atomic Number
Consider the image of an extremity (Figure 9-12). An image of the bone is produced because many more x-rays are absorbed photoelectrically in bone than in soft tissue. Recall that the probability of an x-ray undergoing photoelectric effect is proportional to the third power of the atomic number of the tissue.
FIGURE 9-12 Radiograph of bony structures results from differential absorption between bone and soft tissue.
Bone has an atomic number of 13.8, and soft tissue has an atomic number of 7.4 (see Table 9-3). Consequently, the probability that an x-ray will undergo a photoelectric interaction is approximately seven times greater in bone than in soft tissue.
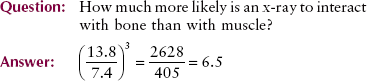
These relative values of interaction are apparent in Figure 9-13 when one pays particular attention to the logarithmic scale of the vertical axis. Note that the relative probability of interaction between bone and soft tissue (differential absorption) remains constant, but the absolute probability of each decreases with increasing energy. With higher x-ray energy, fewer interactions occur, so more x-rays are transmitted without interaction.
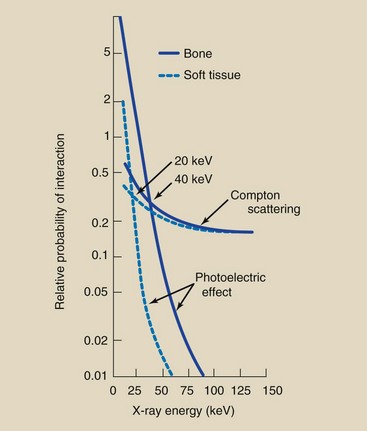
FIGURE 9-13 Graph showing the probabilities of photoelectric and Compton interactions with soft tissue and bone. The interactions of these curves indicate those x-ray energies at which the chance of photoelectric absorption equals the chance of Compton scattering.
Compton scattering is independent of the atomic number of tissue. The probability of Compton scattering for bone atoms and for soft tissue atoms is approximately equal and decreases with increasing x-ray energy.
This decrease in Compton scattering, however, is not as rapid as the decrease in photoelectric effect with increasing x-ray energy. The probability of Compton scattering is inversely proportional to x-ray energy (1/E). The probability of the photoelectric effect is inversely proportional to the third power of the x-ray energy (1/E3).
At low energies, most x-ray interactions with tissue are photoelectric. At high energies, Compton scattering predominates.
Of course, as x-ray energy is increased, the chance of any interaction at all decreases. As kVp is increased, more x-rays penetrate to the image receptor; therefore, a lower x-ray quantity (lower mAs) is required.
Figure 9-13 combines all of these factors into a single graph. At 20 keV, the probability of photoelectric effect equals the probability of Compton scattering in soft tissue. Below this energy, most x-rays interact with soft tissue photoelectrically. Above this energy, the predominant interaction with soft tissue is Compton scattering. Low kVp resulting in increased differential absorption provides the basis for mammography, which is an example of soft tissue radiography.
To image small differences in soft tissue, one must use low kVp to get maximum differential absorption.
The relative frequency of Compton scattering compared with photoelectric effect increases with increasing x-ray energy. The crossover point between photoelectric effect and Compton scattering for bone is approximately 40 keV. Nevertheless, low-kVp technique is usually appropriate for bone radiography to maintain image contrast.
High-kVp technique is usually used for examination of barium studies and chest radiography, in which intrinsic contrast is high, resulting in much lower patient dose.
When high-kVp technique is used in this manner, the amount of scattered radiation from surrounding soft tissue contributes little to the image. When the amount of scattered radiation becomes too great, grids are used (see Chapter 13). Grids do not affect the magnitude of the differential absorption.
Differential absorption in bone and soft tissue results from photoelectric interactions, which greatly depend on the atomic number of tissue. The loss of contrast is due to noise caused by Compton scattering. Two other factors are important in making an x-ray image: x-ray emission spectrum and mass density of patient tissue.
The crossover energies of 20 and 40 keV refer to a monoenergetic x-ray beam, that is, a beam containing x-rays that all have the same energy. In fact, discussed in Chapter 7, clinical x-rays are polyenergetic. They are emitted over an entire spectrum of energies.
The correct selection of voltage for optimum differential absorption depends on the other factors discussed in Chapter 8 that affect the x-ray emission spectrum. For instance, in anteroposterior radiography of the lumbar spine at 110 kVp, a greater number of x-rays are emitted with energy above the 40-keV crossover for bone than below it. Less filtration or a grid may then be necessary.
Dependence on Mass Density
Intuitively, we know that we could image bone even if differential absorption were not Z-related because bone has a higher mass density than soft tissue. Mass density is not to be confused with optical density. Mass density is the quantity of matter per unit volume, specified in units of kilograms per cubic meter (kg/m3). Sometimes mass density is reported in grams per cubic centimeter (g/cm3).
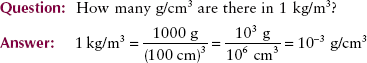
Table 9-5 gives the mass densities of several radiologically important materials. Mass density is related to the mass of each atom and basically tells how tightly the atoms of a substance are packed.
Water and ice are composed of precisely the same atoms, but ice occupies greater volume. The mass density of ice is 917 kg/m3 compared with 1000 kg/m3 for water. Ice floats in water because of this difference in mass density. Ice is lighter than water.
The interaction of x-rays with tissue is proportional to the mass density of the tissue regardless of the type of interaction.
When mass density is doubled, the chance for x-ray interaction is doubled because twice as many electrons are available for interaction. Therefore, even without the Z-related photoelectric effect, nearly twice as many x-rays would be absorbed and scattered in bone as in soft tissue. The bone would be imaged.
The lungs are imaged in chest radiography primarily because of differences in mass density. According to Table 9-5, the mass density of soft tissue is 770 times that of air (1000/1.3) and three times that of lung (1000/320). Therefore, for the same thickness, we can expect almost three times as many x-rays to interact with the soft tissue as with lung tissue.
The Z values of air and soft tissue are about the same: 7.4 for soft tissue and 7.6 for air; thus, differential absorption in air-filled soft tissue cavities is primarily attributable to differences in mass density. Interestingly, air has higher Z than soft tissue because it has more nitrogen. Figure 9-14 demonstrates differential absorption in air, soft tissue, and bone caused by mass density differences. Table 9-6 summarizes the various relationships of differential absorption.
TABLE 9-6
Characteristics of Differential Absorption
| As X-ray Energy Increases | Fewer Compton Interactions |
| Many fewer photoelectric interactions | |
| More transmission through tissue | |
| As tissue atomic number increases | No change in Compton interactions |
| Many more photoelectric interactions | |
| Less x-ray transmission | |
| As tissue mass density increases | Proportional increase in Compton interactions |
| Proportional increase in photoelectric interactions | |
| Proportional reduction in x-ray transmission |
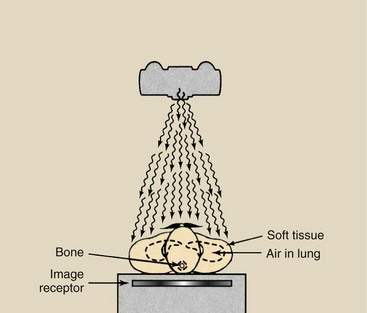
FIGURE 9-14 Even if x-ray interaction were not related to atomic number (Z), differential absorption would occur because of differences in mass density.
Contrast Examinations
Barium and iodine compounds are used as an aid for imaging internal organs with x-rays. The atomic number of barium is 56; that of iodine is 53. Each has a much higher atomic number and greater mass density than soft tissue. When used in this fashion, they are called contrast agents, and because of their high atomic numbers, they are positive contrast agents.
When an iodinated contrast agent fills the internal carotid artery or when barium fills the colon, these internal organs are readily visualized on a radiograph. Low-kVp technique (e.g., <80 kVp) produces excellent, high-contrast radiographs of the organs of the gastrointestinal tract. Higher-kVp operation (e.g., >90 kVp) often can be used in these examinations not only to outline the organ under investigation but also to penetrate the contrast medium so the lumen of the organ can be visualized more clearly.
Air was used at one time as a contrast medium in procedures such as pneumoencephalography and ventriculography. Air is still used for contrast in some examinations of the colon along with barium; this is called a double-contrast examination. When used in this fashion, air is a negative contrast agent.
Exponential Attenuation
When x-rays are incident on any type of tissue, they can interact with the atoms of that tissue through any of these five mechanisms: coherent scattering, Compton scattering, photoelectric effect, pair production, and photodisintegration. The relative frequency of interaction through each mechanism depends on the atomic number of the tissue atoms, the mass density, and the x-ray energy.
An interaction such as the photoelectric effect is called an absorption process because the x-ray disappears. Absorption is an all-or-none condition for x-ray interaction.
Interactions in which the x-ray is only partially absorbed, such as Compton scattering, are only partial absorption processes. Pair production and photodisintegration are absorption processes.
The total reduction in the number of x-rays remaining in an x-ray beam after penetration through a given thickness of tissue is called attenuation. When a broad beam of x-rays is incident on any tissue, some of the x-rays are absorbed, and some are scattered. The result is a reduced number of x-rays, a condition referred to as x-ray attenuation.
X-rays are attenuated exponentially, which means that they do not have a fixed range in tissue. They are reduced in number by a given percentage for each incremental thickness of tissue they go through.
Consider the situation diagrammed in Figure 9-15. One thousand x-rays are incident on a 25-cm-thick abdomen. The x-ray energy and the atomic number of the tissue are such that 50% of the x-rays are removed by the first 5 cm. Therefore, in the first 5 cm, 500 x-rays are removed, leaving 500 available to continue penetration.
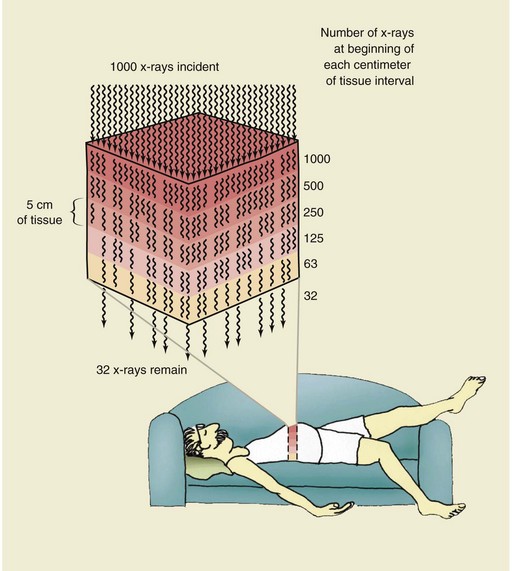
FIGURE 9-15 Interaction of x-rays by absorption and scatter is called attenuation. In this example, the x-ray beam has been attenuated 97%; 3% of the x-rays have been transmitted.
By the end of the second 5 cm, 50% of the 500 or 250 additional x-rays have been removed, leaving 250 x-rays to continue. Similarly, entering the fourth 5-cm thickness are 125 x-rays, and entering the fifth and last 5 cm thickness are 63 x-rays. Half of the 63 x-rays will be attenuated in the last 5 cm of tissue; therefore, only 32 will be transmitted to interact with the image receptor. The total effect of these interactions is 97% attenuation and 3% transmission of the x-ray beam.
A plot of this hypothetical x-ray beam attenuation, which closely resembles the actual situation, appears in Figure 9-16. Is it obvious that the assumed half-value layer in soft tissue was 5 cm? It should be clear that, theoretically at least, the number of x-rays emerging from any thickness of absorber will never reach zero. Each succeeding thickness can attenuate the x-ray beam only by a fractional amount, and a fraction of any positive number is always greater than zero.
FIGURE 9-16 Linear and semilog plots of exponential x-ray attenuation data in Figure 9-15.
This is not the way that alpha particles and beta particles interact with matter. Regardless of the energy of the particle and the type of tissue, these particulate radiations can penetrate only so far before they are totally absorbed. For example, beta particles with 2 MeV of energy have a range of approximately 1 cm in soft tissue.
Summary
Following are five fundamental interactions between x-rays and matter:
1. Coherent scattering is a change in the direction of an incident x-ray without a loss of energy.
2. Compton scattering occurs when incident x-rays ionize atoms and the x-ray then changes direction with a loss of energy.
3. The photoelectric effect occurs when the incident x-ray is absorbed into one of the inner electron shells and emits a photoelectron.
4. Pair production occurs when the incident x-ray interacts with the electric field of the nucleus. The x-ray disappears, and two electrons appear—one positively charged (positron) and one negatively charged (electron).
5. Photodisintegration occurs when the incident x-ray is directly absorbed by the nucleus. The x-ray disappears, and nuclear fragments are released.
The interactions that are important to diagnostic x-ray imaging are Compton scattering and the photoelectric effect.
Differential absorption controls the contrast of an x-ray image. The x-ray image results from the difference between those x-rays absorbed by photoelectric interaction and those x-rays that pass through the body as image-forming x-rays. Attenuation is the reduction in x-ray beam intensity as it penetrates through tissue. Differential absorption and attenuation of the x-ray beam depend on the following factors:
Radiologic contrast agents, such as iodine and barium, use the principles of differential absorption to image soft tissue organs. Iodine is used in vascular, renal, and biliary imaging. Barium is used for gastrointestinal imaging. Both elements have high atomic numbers (iodine’s is 53, and barium’s is 56) and mass density much greater than that of soft tissue.
1. Define or otherwise identify the following:
2. What are the two factors of importance to differential absorption?
3. A 28-keV x-ray interacts photoelectrically with a K-shell electron of a calcium atom. What is the kinetic energy of the secondary electron (see Table 2-3)?
4. 1000 x-rays with energy of 140 keV are incident on bone and soft tissue of equal thickness. If 87 x-rays are scattered in soft tissue, approximately how many are scattered in bone?
5. Why are iodinated compounds such excellent agents for vascular contrast examinations?
6. Diagram Compton scattering; identify the incident x-ray, positive ion, negative ion, and scattered x-ray.
7. Describe backscatter radiation. Can you think of examples in diagnostic radiology?
8. Tungsten is sometimes alloyed into the beam-defining collimators of an x-ray imaging system. If a 63-keV x-ray undergoes a Compton interaction with an L-shell electron and ejects that electron with 12 keV of energy, what is the energy of the scattered x-ray (see Figure 2-9)?
9. Of the five basic mechanisms of x-ray interaction with matter, three are not important to diagnostic radiology. Which are they, and why are they not important?
10. On average, 33.7 eV is required for each ionization in air. How many ion pairs would a 22-keV x-ray probably produce in air, and approximately how many of these would be produced photoelectrically?
11. How is the energy of the Compton-scattered x-ray computed?
12. Does the probability of Compton scattering depend on the atomic number of the target atom?
13. When kVp is increased, is Compton scattering increased or reduced?
14. Describe the photoelectric effect.
15. When kVp is increased, what happens to the absolute probability of the photoelectric effect versus Compton scattering?
16. How much more likely is it that an x-ray will interact with bone than with muscle?
17. What is the relationship between atomic number (Z) and differential absorption?
18. What is the relationship between mass density and differential absorption?
19. In a contrast radiographic examination with iodine, what is the relative probability that x-rays will interact with iodine rather than with soft tissue?
20. What kVp is used to penetrate barium in a contrast examination?
The answers to the Challenge Questions can be found by logging on to our website at http://evolve.elsevier.com.