Fundamental Principles of Radiobiology
At the completion of this chapter, the student should be able to do the following:
1 State the law of Bergonie and Tribondeau.
2 Describe the physical factors that affect radiation response.
3 Describe the biologic factors that affect radiation response.
4 Explain radiation dose-response relationships.
5 Describe five types of radiation dose-response relationships.
SOME TISSUES are more sensitive than others to radiation exposure. Such tissues usually respond more rapidly and to lower doses of radiation.
REPRODUCTIVE CELLS are more sensitive than nerve cells. This and other radiobiologic concepts were detailed in 1906 by two French scientists.
PHYSICAL FACTORS and biologic factors affect the radiobiologic response of tissue. Knowledge of these radiobiologic factors is essential for understanding the positive effects of radiation oncology and the potentially harmful effects of low-dose radiation exposure.
THE PRINCIPAL aim of the study of radiobiology is to understand radiation dose–response relationships. A dose-response relationship is a mathematical and graphic function that relates radiation dose to observed response.
Law of Bergonie and Tribondeau
In 1906, two French scientists, Bergonie and Tribondeau, theorized and observed that radiosensitivity was a function of the metabolic state of the tissue being irradiated. This has come to be known as the law of Bergonie and Tribondeau and has been verified many times. Basically, the law states that the radiosensitivity of living tissue varies with maturation and metabolism (Box 30-1).
This law is principally interesting as a historical note in the development of radiobiology. It has found some application in radiation oncology. In diagnostic imaging, the law serves to remind us that fetuses are considerably more sensitive to radiation exposure as are children compared with the mature adults.
Physical Factors that Affect Radiosensitivity
When one irradiates tissue, the response of the tissue is determined principally by the amount of energy deposited per unit mass—the radiation dose in Gyt (rad). Even under controlled experimental conditions, however, when equal doses are delivered to equal specimens, the response may not be the same because of other modifying factors. A number of physical factors affect the degree of radiation response.
Linear Energy Transfer
Linear energy transfer (LET) is a measure of the rate at which energy is transferred from ionizing radiation to soft tissue. It is another method of expressing radiation quality and determining the value of the radiation weighting factor (WR) used in radiation protection (see Chapter 35). LET is expressed in units of kiloelectron volt of energy transferred per micrometer of track length in soft tissue (keV/µm).
The ability of ionizing radiation to produce a biologic response increases as the LET of radiation increases. When LET is high, ionizations occur frequently, increasing the probability of interaction with the target molecule.
Relative Biologic Effectiveness
As the LET of radiation increases, the ability to produce biologic damage also increases. This effect is quantitatively described by the relative biologic effectiveness (RBE).
The standard radiation, by convention, is orthovoltage x-radiation in the range of 200 to 250 kVp. This type of x-ray beam was used for many years in radiation oncology and in essentially all early radiobiologic research.
Diagnostic x-rays have an RBE of 1. Whereas radiations with lower LET than diagnostic x-rays have an RBE less than 1, radiations with higher LET have a higher RBE.
Figure 30-1 shows the relationship between RBE and LET and identifies some of the more common types of radiation. Table 30-1 lists the approximate LET and RBE of various types of ionizing radiation.
TABLE 30-1
Linear Energy Transfer and Relative Biologic Effectiveness of Various Radiation Doses
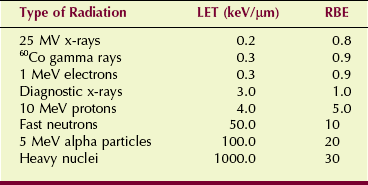
LET, Linear energy transfer; RBE, relative biologic effectiveness.
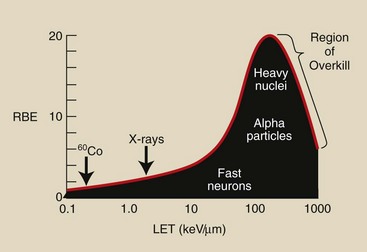
FIGURE 30-1 As linear energy transfer (LET) increases, relative biologic effectiveness (RBE) also increases, but a maximum value is reached followed by a lower RBE because of overkill.
Protraction and Fractionation
If a dose of radiation is delivered over a long period of time rather than quickly, the effect of that dose is less. Stated differently, if the time of irradiation is lengthened, a higher dose is required to produce the same effect. This lengthening of time can be accomplished in two ways.
If the dose is delivered continuously but at a lower dose rate, it is said to be protracted. Six gray (600 rad) delivered in 3 -minutes at a dose of 2 Gyt/min is lethal for a mouse. However, when 6 Gyt is delivered at the rate of 10 mGyt/hr for a total time of 600 hours, the mouse will survive.
If the 6-Gyt dose is delivered at the same dose rate, but in 12 equal fractions of 500 mGyt, all separated by 24 hours, the mouse will survive. In this situation, the dose is said to be fractionated.
Radiation dose fractionation reduces effect because cells undergo repair and recovery between doses. Dose fractionation is used routinely in radiation oncology.
Biologic Factors that Affect Radiosensitivity
In addition to these physical factors, a number of biologic conditions alter the radiation response of tissue. Some of these factors, such as age and metabolic rate, have to do with the inherent state of tissue. Other factors are related to artificially introduced modifiers of the biologic system.
Oxygen Effect
Tissue is more sensitive to radiation when irradiated in the oxygenated, or aerobic, state than when irradiated under anoxic (without oxygen) or hypoxic (low-oxygen) conditions. This characteristic of tissue radiation response is called the oxygen effect and is described numerically by the oxygen enhancement ratio (OER).
Generally, tissue irradiation is conducted under conditions of full oxygenation. Hyperbaric (high-pressure) oxygen has been used in radiation oncology in an attempt to enhance the radiosensitivity of nodular, avascular tumors, which are less radiosensitive than tumors with an adequate blood supply.

The OER is LET dependent (Figure 30-2). The OER is highest for low-LET radiation, with a maximum value of approximately 3 that decreases to approximately 1 for high-LET radiation.
Age
The age of a biologic structure affects its radiosensitivity. The response of humans is characteristic of this age-related radiosensitivity (Figure 30-3). Humans are most sensitive before birth.
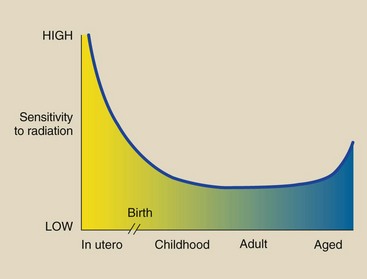
FIGURE 30-3 Radiosensitivity varies with age. Experiments with animals have shown that very young and very old individuals are more sensitive to radiation.
After birth, sensitivity decreases until maturity, at which time humans are most resistant to radiation effects. In old age, humans again become somewhat more radiosensitive.
Recovery
In vitro experiments show that human cells can recover from radiation damage. If the radiation dose is not sufficient to kill the cell before its next division (interphase death), then given sufficient time, the cell will recover from the sublethal radiation damage it has sustained.
This intracellular recovery is attributable to a repair mechanism inherent in the biochemistry of the cell. Some types of cells have greater capacity than others for repair of sublethal damage. At the whole-body level, this recovery from radiation damage is assisted through repopulation by surviving cells.
If a tissue or organ receives a sufficient radiation dose, it responds by shrinking. This is called atrophy, and it occurs because some cells die and disintegrate and are carried away as waste products.
If a sufficient number of cells sustain only sublethal damage and survive, they may proliferate and repopulate the irradiated tissue or organ.
Chemical Agents
Some chemicals can modify the radiation response of cells, tissues, and organs. For chemical agents to be effective, they must be present at the time of irradiation. Postirradiation application does not usually alter the degree of radiation response.
Radiosensitizers
Agents that enhance the effect of radiation are called sensitizing agents. Examples include halogenated pyrimidines, methotrexate, actinomycin D, hydroxyurea, and vitamin K.
The halogenated pyrimidines become incorporated into the DNA of the cell and amplify the effects of radiation on that molecule. All radiosensitizers have an effectiveness ratio of approximately 2, that is, if 90% of a cell culture is killed by 2 Gyt (200 rad), then in the presence of a sensitizing agent, only 1 Gyt (100 rad) is required for the same percentage of lethality.
Radioprotectors
Radioprotective compounds include molecules that contain a sulfhydryl group (sulfur and hydrogen bound together), such as cysteine and cysteamine. Hundreds of others have been tested and found effective by a factor of approximately 2. For example, if 6 Gyt (600 rad) is a lethal dose to a mouse, then in the presence of a radioprotective agent, 12 Gyt (1200 rad) would be required to produce lethality.
Radioprotective agents have not found human application because, to be effective, they must be administered at toxic levels. The protective agent can be worse than the radiation!
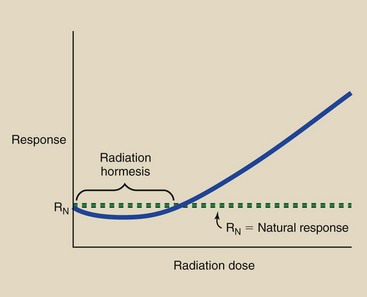
Hormesis
A separate and small body of radiobiologic evidence suggests that a little bit of radiation is good for you. Some studies have shown that animals given low radiation doses live longer than controls. The prevailing explanation is that a little radiation stimulates hormonal and immune responses to other toxic environmental agents.
Many nonradiation examples of hormesis can be found. In large quantities, fluoride is deadly. In small quantities, it is a known tooth preservative.
Regardless of radiation hormesis, we continue to practice ALARA (“as low as reasonably achievable”) vigorously as a known safe approach to radiation management.
Radiation Dose-Response Relationships
Although some scientists were working with animals to observe the effects of radiation a few years after the discovery of x-rays, these studies were not experimentally sound, nor were their results applied. With the advent of the age of the atomic bomb in the 1940s, however, interest in radiobiology increased enormously.
The object of nearly all radiobiologic research is the establishment of radiation dose-response relationships. A radiation dose-response relationship is a mathematical relationship between various radiation dose levels and magnitude of the observed response.
Radiation dose-response relationships have two important applications in radiology. First, these experimentally determined relationships are used to design therapeutic treatment routines for patients with cancer.
Radiobiologic studies also have been designed to yield information on the effects of low-dose irradiation. These studies and the dose-response relationships revealed provide the basis for radiation management activities and are particularly significant for diagnostic radiology.
Human responses to radiation exposure fall into two types: early or late, high dose or low dose, and deterministic or stochastic. Deterministic radiation responses usually follow high-dose exposure and an early response. Radiation-induced skin burns represent a deterministic response.
Stochastic responses are cancer, leukemia, or genetic effects. Such responses usually follow low radiation exposure and appear as a late radiation response.
Every radiation dose-response relationship has two characteristics. It is either linear or nonlinear, and it is either threshold or nonthreshold. These characteristics can be described mathematically or graphically. The following discussion avoids the math.
Linear Dose-Response Relationships
Figure 30-4 shows examples of the linear dose-response relationship, which is so named because the response is directly proportionate to the radiation dose. When the radiation dose is doubled, the response to radiation likewise is doubled.
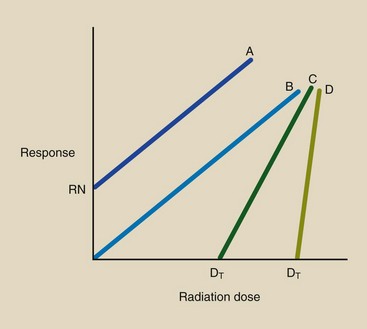
FIGURE 30-4 Linear dose-response relationships A and B are nonthreshold types; C and D are threshold types. RN is the normal incidence or response with no radiation exposure.
Dose-response relationships A and B intersect the dose axis at zero or below (see Figure 30-4). These relationships are therefore the linear, nonthreshold type. In a nonthreshold dose-response relationship, any dose, regardless of its size, is expected to produce a response.
At zero dose, relationship A exhibits a measurable response, RN. The level RN, called the natural response level, indicates that even without radiation exposure, that type of response, such as cancer, occurs.
Dose-response relationships C and D are identified as linear, threshold because they intercept the dose axis at some value greater than zero. The threshold dose for C and D is DT.
At radiation doses below DT, no response is observed. Relationship D has a steeper slope than C; therefore, above the threshold dose, any increment of dose produces a larger response if that response follows relationship D rather than C.
Nonlinear Dose-Response Relationships
All other radiation dose-response relationships are nonlinear (Figure 30-5). Curves A and B are nonlinear, nonthreshold. Curve A shows that a large response results from a very small radiation dose. At high dose levels, radiation is not so efficient because an incremental dose at high levels results in less relative damage than the same incremental dose at low levels.
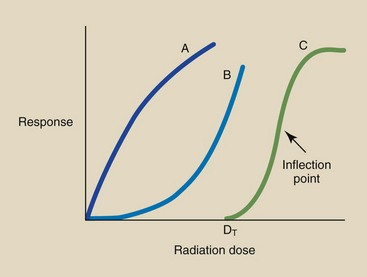
FIGURE 30-5 Nonlinear dose-response relationships can assume several shapes. Curves A and B are nonthreshold. Curve C is nonlinear, threshold. DT, Threshold dose.
The dose-response relationship represented by curve B is just the opposite. Incremental doses in the low dose range produce very little response. At high doses, however, the same increment of dose produces a much larger response.
Curve C is a nonlinear, threshold relationship. At doses below DT, no response is measured. As the dose is increased to above DT, it becomes increasingly effective per increment of dose until the dose that corresponds to the inflection point of the curve is reached. This type of dose-response relationship is characteristic of a deterministic response.
The inflection point occurs when the curve stops bending up and begins bending down. Above this level, incremental doses become less effective. Relationship C is sometimes called an S-type, or sigmoid type, radiation dose-response relationship.
We shall refer to these general types of radiation dose-response relationships when discussing the type and degree of human radiation injury. Diagnostic radiology is concerned almost exclusively with the late effects of radiation exposure and therefore with linear, nonthreshold dose-response relationships. For completeness, however, Chapter 33 briefly discusses early radiation damage.
Constructing a Dose-Response Relationship
Determining the radiation dose-response relationship for a whole-body response is tricky. It is very difficult to determine the degree of response, even that of early effects, because the number of experimental animals that can be used is usually small. It is nearly impossible to measure low-dose, stochastic effects—the area of greatest interest in diagnostic imaging.
Therefore, we resort to irradiating a limited number of animals to very large doses of radiation in the hope of observing a statistically significant response. Figure 30-6 shows the results of such an experiment in which four groups of animals were irradiated to a different dose. The observations on each group result in an ordered pair of data: a radiation dose and the associated biologic response.
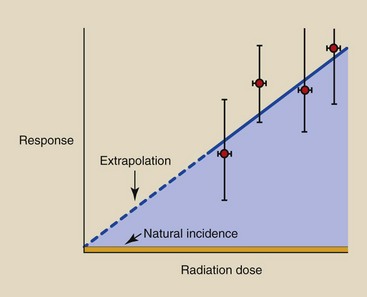
FIGURE 30-6 A dose-response relationship is produced when high-dose experimental data are extrapolated to low doses.
The error bars in each ordered pair indicate the confidence associated with each data point. Error bars on the dose measurements are very narrow; thus, we can measure radiation dose very accurately. Error bars on the response, however, are very wide because of biologic variability and the limited number of observations at each dose.
The principal interest in diagnostic imaging is to estimate response at very low radiation doses. Because this cannot be done directly, we extrapolate the dose-response relationship from the high-dose, known region into the low-dose, unknown region.
This extrapolation invariably results in a linear, nonthreshold dose-response relationship. Such an extrapolation, however, may not be correct because of the many qualifying conditions on the experiment.
The radiation dose-response relationship that demonstrates radiation hormesis appears as in Figure 30-7. At very low doses, irradiated subjects experience less response than control participants. The existence of radiation hormesis is a highly controversial topic in radiologic science. Regardless of its existence, no human radiation responses have been observed after radiation doses less than 100 mGyt (10 rad).
Summary
In 1906, two French scientists first theorized that radiosensitivity was a function of the metabolic state of tissue being irradiated. Their theories, known as the law of Bergonie and Tribondeau, state the following: (1) Stem cells are radiosensitive, and mature cells are less so; (2) young tissue is more radiosensitive than older tissue; (3) high metabolic activity is radiosensitive, and low metabolic rate is radioresistant; and (4) increases in proliferation and growth rates of cells make them more radiosensitive.
Physical and biologic factors affect tissue radiosensitivity. Physical factors include LET, RBE, fractionation, and protraction. Biologic factors that affect radiosensitivity include the oxygen effect, the age-related effect, and the recovery effect.
Some chemicals can modify cell response. These are called radiosensitizers and radioprotectors.
Radiobiologic research concentrates on radiation dose-response relationships. In linear dose-response relationships, the response is directly proportional to the dose. In nonlinear dose-response relationships, varied doses produce varied responses.
The threshold dose is the level below which there is no response. The nonthreshold dose-response relationship means that any dose is expected to produce a response. For establishing radiation protection guidelines for diagnostic imaging, the linear, nonthreshold dose-response model is used.
1. Define or otherwise identify the following:
2. Write the formula for relative biologic effectiveness.
3. Give an example of fractionated radiation.
4. Why is high-pressure (hyperbaric) oxygen used in radiation oncology?
5. Write the formula for the oxygen enhancement ratio.
6. How does age affect the radiosensitivity of tissue?
7. When a radiobiologic experiment is conducted in vitro, what does this mean?
8. Name three agents that enhance the effects of radiation.
9. Name three radioprotective agents.
10. Are radioprotective agents used for human application?
11. Explain the meaning of a radiation dose-response relationship.
12. What occurs in a nonlinear radiation dose-response relationship?
13. Explain why the linear, nonthreshold dose-response relationship is used as a model for diagnostic imaging radiation management.
14. State two of the corollaries to the law of Bergonie and Tribondeau.
15. Approximately 8 Gyt of 220 kVp x-rays is necessary to produce death in an armadillo. Cobalt-60 gamma rays have a lower LET than 220 kVp x-rays; therefore, 9.4 Gyt is required for armadillo lethality. What is the RBE of 60CO compared with 220 kVp?
16. Under fully oxygenated conditions, 90% of human cells in culture will be killed by 1.5 Gyt x-rays. If cells are made anoxic, the dose required for 90% lethality is 4 Gyt . What is the OER?
17. What are the units of LET?
18. Describe how RBE and LET are related.
19. Is occupational radiation exposure fractionated, protracted, or continuous?
The answers to the Challenge Questions can be found by logging on to our website at http://evolve.elsevier.com.