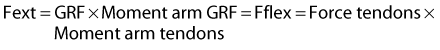Chapter 26 The Biomechanics of the Equine Limb and Its Effect on Lameness
Biological structures (and sometimes those engineered by man) break, as a result of either a one-off (single event) load that exceeds their mechanical capacity or, more commonly, chronic fatigue overload, in which repeat microfailures over time lead to failure of the whole structure. Biological tissue has the unique ability to adapt to mechanical demands and to repair itself given an appropriate mechanical stimulus and sufficient time. Complete failure of a structure happens only if the damage over time exceeds adaptation and repair.
Like man-made structures (e.g., elevators, bridges), biological designs have an inherent safety factor, defined as the ratio of the maximum stress a structure could withstand until breakage and the stress it is most likely to undergo during its lifetime. It is rather comforting that most engineered devices have a safety factor of up to 10 (so next time you read that an elevator has a maximum capacity of 18 people, know that it would actually hold 180!). Unfortunately, the safety factors1 of equine bones and tendons are approximately 1.5 to 2.
Box 26-1 provides short definitions of biomechanical terms used in this chapter.
BOX 26-1 Definition of Common Terms in Biomechanics
When Do Musculoskeletal Structures Fail?
The parameters that influence failure of a musculoskeletal element are the force (magnitude, frequency and number of cycles, speed and duration of loading) the structure experiences and its ability to withstand it. The force on an individual part is related to the force that the whole limb experiences. Force is determined by body mass, speed of locomotion, and the leverage that force has on the specific part. A structure’s ability to withstand force is determined by its structural properties, which in turn depend on its material properties and its dimensions. These reflect the magnitude and direction of the forces acting on it. Forces causing deformation include tension, compression, bending, and shear. Most structures are subjected to and are optimized for one predominant force, but they also have to be able to withstand other forces in normal use and even more so in exceptional circumstances. Tendons experience predominantly tensile forces, whereas joints are subjected to mainly compressive and some shear forces. Bones experience bending, with compressive forces on the concave side and tensile forces on the convex side. Bones have to withstand not only compressive forces from the horse’s weight, but also the forces exerted by muscles and tendons that attach to them.
Failure in a live horse is much more complex than simple mechanics, because adaptation, repair, and compensatory mechanisms must be considered. Lameness may be not only a response to pain but also a compensatory mechanism, because it often results in an unloading of the affected limb or structure.
Elements of the musculoskeletal system have to fulfill four main requirements: force transmission without excessive deformation and fracture; use of the least amount of material to keep the metabolic costs for maintenance, transport, and regeneration down; and enough reserve of strength to cope with overload in the case of an accident.2 Thus there is a trade-off between safety factors and energy costs. In horses the balance is shifted in favor of keeping the energy costs low while accepting a relatively high risk of musculoskeletal injury. Tendons (such as the equine digital flexor tendons or the human Achilles tendon) need to stretch to store energy in locomotion; to perform this role they need to reach high strains, which places them at a high risk for mechanical overload and damage.
In the following sections we describe the functional anatomy of the horse’s limb and the material properties of its components. We discuss the influence of locomotion and the effects of conformation and farriery intervention on the loads acting on the musculoskeletal elements, such as bones, tendons, and joints. We also consider how the loads acting on the musculoskeletal system are changed with certain musculoskeletal disorders.
Functional Anatomy of the Horse Limb
Horses have the ability to run fast over short distances (racing speeds reach 21 m/sec [75 km/hr]) and also to cover long distances at slower speeds with a low energy cost of locomotion. This was of evolutionary advantage because it enabled them not only to outrun predators but also to migrate to forage on the rather sparsely vegetated prairie land they originally inhabited. To achieve two diverse locomotive requirements, the horse developed anatomical features that promoted energy efficiency (after all, it would not do the horse any good if it had to spend more energy to get to the food than could be gained by eating the food, or to get eaten in the process).
Although most veterinarians are familiar with some energy-saving mechanisms, such as the unguligrade stance of the horse, the patellar locking mechanism, and the stay (reciprocal) apparatus, from standard textbooks, there are many more features that play a major role in ensuring energy-efficient locomotion. This section concentrates on the musculoskeletal adaptations of the equine limb; however, a more comprehensive overview of general anatomical features is given elsewhere.3
Horse Limbs Function Like Pogo Sticks
If you tried to build a horse limb with children’s blocks, the limb would collapse, because it would be impossible to build the fetlock joint in a hyperextended position. However, in a live limb the digital flexor tendons and ligaments on the flexor side of the limb prevent failure. Tendons have elastic properties and act like rubber bands or springs, providing resistance against which the limb presses when it comes under load, thus resisting further hyperextension and preventing collapse (Figure 26-1). The tendons are stretched at the same time, thus storing elastic strain energy, which can be returned in elastic recoil. During each step energy is stored, and it is returned when the limb leaves the ground. Energy is carried forward from one step to the next, thus reducing work the muscles have to do and saving metabolic energy. Indeed, the muscles associated with the main contributors of this system—the suspensory ligament (SL), deep digital flexor tendon (DDFT), and superficial digital flexor tendon (SDFT)—either are not present at all (the SL and the accessory ligament of the DDFT [ALDDFT]) or are very short in relation to the tendons (e.g., the average length of the deep digital flexor muscle-tendon unit in a Thoroughbred is 77 ± 5 cm, more than 60% of which is tendon. The flexor muscles, being highly pennate and having short muscle fibers (1 cm in length), have limited capacity to change the length of the muscle-tendon unit when contracting. Approximately 7% of the energy stored in the tendons is released as heat, and during gallop the tendons of a galloping horse reach about 45°C.4 We have reasoned that increase in temperature may account for core lesions in equine SDFTs but found that although 45°C resulted in death of some cells, tendon cells may be resistant.5 Core lesions may result from hyperthermic damage of matrix components.5
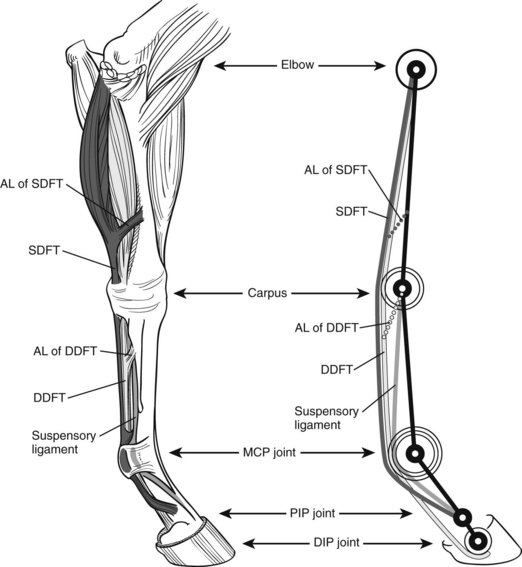
Fig. 26-1 Anatomical drawing of an equine forelimb (left) and the equine forelimb modeled as a spring-system (right); superficial digital flexor tendon (SDFT); deep digital flexor tendon (DDFT); accessory ligament (AL) of the DDFT; and AL of the SDFT. Limbs function like pogo sticks: the hyperextended fetlock joint is kept from collapsing by the springlike digital flexor tendons on the palmar aspect of the limb. When the limb comes under load during the stance phase of the stride, it compresses by further extending the fetlock joint while stretching the digital flexor tendons. This enables the digital flexor tendons to store elastic energy, which is released for propelling the limb into the swing phase. MCP, Metacarpophalangeal; PIP, proximal interphalangeal; DIP, distal interphalangeal.
Like any springlike structure, the limb itself has a certain stiffness, which is a measure of how much it shortens for a given load. A whole equine limb changes length mainly as a result of fetlock extension and length changes in the digital flexor tendons.6 People can adjust their leg stiffness by muscle contraction to suit the softness or hardness of the ground on which they are walking or running.7 Horses cannot adjust their leg stiffness because of the limited ability of the flexor muscles/tendons to change length, and this may be the reason why some horses cope better than others on different goings (footings). The flexor muscles do, however, damp vibrations, which otherwise would be likely to cause injury to musculoskeletal tissues.8
Bones
To enable a pogo-stick design, the bones in the equine limb are reduced compared with other animals: the radius and ulna are fused, and the horse bears weight only on the third metacarpal bone (McIII) or third metatarsal bone and the digit. Fewer bones allow lengthening of the limb and tendons and reduction of the mass of the distal aspect of the limb. This increases the energy storage capabilities of the digital flexor tendons and also results in a lighter limb that can be swung more rapidly and with less energetic cost, which is of benefit in locomotion. Fewer bones is thus an adaptation for maximum strength with minimum weight, because the bending strength is much higher for one large bone than for the same amount (and hence weight) of material arranged as several smaller bones.2 However, a reduction in bone mass for energy efficiency results in an increase in fracture risk, and this is reflected in the fact that the distal limb bones are at higher risk for fracture than the proximal limb bones.9
Synovial Joints
Joints fulfill two main mechanical functions: they allow the movement of limb segments in relation to each other, and they act as shock absorbers. Limb movement is limited to the sagittal plane by anatomical adaptations of the phalanges and the fusion of bones, and only small, out-of-plane movements, such as adduction and abduction or rotation, are possible. Movement is further limited by the anatomical features of some of the articular surfaces, such as the interlocking configuration of trochlear and sagittal ridges and matching grooves, and is enforced by collateral ligaments. Without the need for muscular control, these features restrict joint movement to the sagittal plane, thus further decreasing metabolic costs.
Although all joints provide movement and shock absorption to a certain degree, some joints allow only a small range of movement and have the primary function of shock absorption, whereas other joints have a large range of movement and a primary function of movement. These joints can be functionally classified as low-motion or high-motion joints, respectively. The fetlock joint, a good example of a high-motion joint, goes through 90 degrees of movement during the stance phase of gallop, whereas the proximal interphalangeal joint has a range of motion of only 5 to 10 degrees. In complex joints such as the carpus and tarsus, there is a division in function: both the antebrachiocarpal and tarsocrural joints are high-motion joints, but in the more distal joints of the carpus and tarsus there is less movement; the least movement is in the carpometacarpal and tarsometatarsal joints. There is also a difference in occurrence and clinical severity of skeletal disorders between high- and low-motion joints. Osteochrondrosis is much more common in high-motion joints, and osteoarthritis (OA) is usually of greater clinical significance than in low-motion joints.
The Foot as Interface to the Ground
The foot provides the interface between the horse and the ground. It is a complex modification of integument surrounding, supporting, and protecting structures in the distal limb of the horse. The hoof capsule encases within a confined space three bones, a series of ligaments and tendons, two synovial structures, a digital cushion, cartilages of the foot, blood vessels, and nerves. Although the horny hoof capsule provides protection of the internal structures, it does not allow for expansion through swelling; therefore any swelling that does occur as a result of injury leads to an increase in pressure and thus stimulation of pain receptors. Mechanically the foot has three main functions: shock absorption when the foot comes into contact with the ground, support and grip when the limb is bearing weight, and propulsion when the limb leaves the ground. It must also resist excessive abrasion and protect sensitive structures lying internally, while, in wild horses, allowing sufficient natural wear of the wall to maintain hoof shape.10
The foot has a series of “built-in” protective mechanisms that absorb part of the concussive forces and damp vibrations during impact (Figure 26-2):
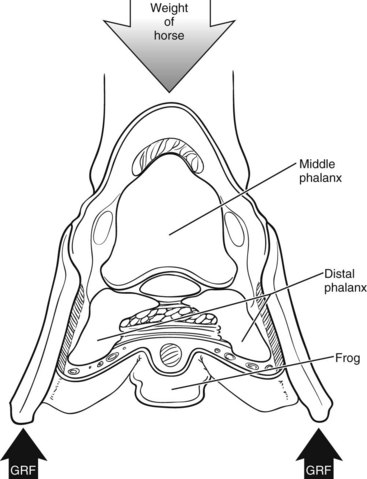
Fig. 26-2 Schematic drawing illustrating two of the shock-absorbing features of the equine foot. First, the shape of the solar surface with the frog in the middle and the frog grooves on either side allows the heels to move sideways and distally on ground contact, while the toe retracts. Second, the suspension of the distal phalanx within the horn capsule allows forces to be transferred from the distal phalanx across the laminar junction to the hoof and to the ground via the distal border of the hoof wall. GRF, Ground reaction force.
Ability of Structures to Cope with Mechanical Demands
Structural and Material Properties
When a force is applied to a structure, the structure usually responds by deforming. The greater the force applied to a structure, the greater the deformation. The ability of a structure to resist deformation is expressed as stiffness and represents the slope of a structure’s force-length relationship. The force-deformation relationship of biological structures behaves in a roughly linear elastic manner until the applied load causes nonreversible deformation and ends in failure. The force-deformation relationship describes the structural properties and depends on the material properties of a tendon and on its dimensions. Larger structures are able to cope with larger forces: imagine two ropes made of the same material, but double the cross-sectional area (approximately 1.41 times the diameter): the thicker rope will be able to withstand double the force of the thinner one.
It is often of interest to know about the properties of the material per se, independent of size. This is achieved by dividing the force acting on a structure by its cross-sectional area. When normalized for cross-sectional area, a force is called stress (σ; common units would be mega Newtons per square meter [MN/m2] or Newtons per square millimeter [N/mm2]). The resulting deformation of an applied stress is expressed as strain (ε), the ratio of the change in size to the original size. Being a ratio, strain does not have a dimension; however, it is often expressed as a percentage—for example, ε = 0.1 = 10%. If we are interested in the property of a material rather than structure, we can express this relationship as a stress-strain curve. The slope of this curve is the ratio between the tensile stress and strain and is called the elastic modulus or Young’s modulus (E). The elastic modulus defines whether a material is “rigid” or “compliant.” Rigid materials have a very high elastic modulus and deform very little under load, whereas compliant materials have a low elastic modulus and require less load to deform. Bone, for example, is relatively rigid, whereas articular cartilage is more compliant and thus is able to act as an excellent shock absorber by undergoing considerable deformation when under load. Figure 68-1 shows the stress-strain curves for the digital flexor tendons of a Thoroughbred racehorse.
The ability of structures to deform when loaded and return to their original length when the load is removed allows them to store energy. The amount of energy per unit volume is the area under the linear portion of the stress-strain curve. The capacity of a material to absorb and release energy is often referred to as elastic resilience. The energy a material can absorb before failure defines whether it is “brittle” or “tough”: tough materials are able to absorb considerable elastic energy before failing, whereas brittle materials absorb very little. The digital flexor tendons of a horse are able to store and return a considerable amount of energy during locomotion. Load-deformation curves of tendons are different between loading and unloading, forming a “hysteresis” loop. The area of the loop presents the loss of energy, largely in the form of heat, that occurs during stretch and release (see Figure 68-2). It has been shown that the heat produced by repetition of this mechanism leads to an increase in core temperature, which may contribute to the pathogenesis of tendon injury through thermal damage.4 A detailed description of the pathobiology of tendon injuries is given in Chapter 68.
From an injury perspective, stress is probably the most informative mechanical measure in addition to strain. Equine digital flexor tendons, for example, have different elastic moduli and experience different strain rates in vivo, but they also have different cross-sectional areas. Both the SL and the SDFT experience high strains (up to 16%) during locomotion, but the stress in the SDFT is much higher than in the SL because its cross-sectional area is only about a third of that of the SL.11 This corresponds to the fact that the SDFT is the most commonly injured tendon or ligament (see Chapter 68).
Changes in Structural Properties
Structural properties change constantly (within limits) either through changes in dimensions or material properties, and this is likely to have an effect on the risk of musculoskeletal injury. Structural properties change with age, in response to loading, and through pathological processes. Changes in dimensions are most obvious for muscle, where exercise leads to an increase in muscle volume. Change in the external dimensions of bones, tendons, and ligaments is limited. These tissues, especially bone, respond predominantly by modifying internal structure. Most biological materials have a variety of components, each of different stiffness—for example, in the case of bone, collagen fibers, and minerals. Mechanical properties can be altered by changing the relative quantity of the components. For example, bone becomes stiffer with higher mineral content, which makes it stronger but diminishes its capacity to absorb energy on impact, making it more brittle. This suggests that there is a trade-off among stiffness, strength, and energy absorption. Chapter 68 summarizes how an equine digital flexor tendon responds to external stimuli.
Not all biological tissues react to stimuli in the same way. Tissue-specific responses play a role both in the pathogenesis of musculoskeletal injury and in how training and rehabilitation programs are designed. Problems can develop when a regimen designed to increase, for example, bone strength may be counterproductive for tendons or joints.
Locomotion and Its Effect on Musculoskeletal Tissues
For quantification purposes, locomotion can be divided into strides: a complete cycle of footfalls (e.g., from the time the left front foot hits the ground to the next time it hits the ground). Each stride can be subdivided into the time the foot spends on the ground (stance phase) and the time the foot is in the air (protraction or swing phase). The ratio between these two is often calculated as a dimensionless parameter for gait characterization and is called the duty factor. In relation to (distal-limb–related) lameness, the stance phase is of more interest than the swing phase because the load on the limb is highest during that time. The stance phase can be divided into three main parts: impact, loading, and propulsion.
When the limb is on the ground it experiences a force, the ground reaction force (GRF) (Figures 26-3 and 26-4). The GRF is a function of mass and gravitational force (F = mass × acceleration), has a magnitude and direction, and is usually described as a vector. The point underneath the foot where the force is applied is called the point of zero moment (PZM). The PZM and the direction and magnitude of the force vector change during the period of the stance phase. Depending on the PZM and the direction of the GRF vector, the force vector does not necessarily go straight through the center of rotation of the joints but might be located dorsally or cranially to it. This creates a lever for the GRF (commonly referred to as the moment arm) acting on the joint. The resulting rotational force (also called torque) causes the joints in the distal aspect of the limb to extend. This extension moment is counteracted by a flexor moment created by the digital flexor tendons and their moment arms on the palmar or plantar aspect of the limb (Figure 26-5). To prevent the limb from collapsing, the extensor moment has to equal the flexor moment:
Fig. 26-3 Ground reaction forces (GRFs) for subsequent forelimb (left “humps”) and hindlimb (right “humps”) stance phases in walk (A) and trot (B) for a 420-kg horse. Solid lines represent vertical force, short-dashed lines craniocaudal force, and long-dashed lines mediolateral force. For walk and trot, vertical peak force and impulse (area under the curve) are higher in the forelimb than in the hindlimb. Craniocaudal force shows the typical sinusoidal shape with decelerative (negative) force in the first half of stance and accelerative (positive) force in the second half. Mediolateral force is generally low in value and often more variable than the other two components of GRF. A, Walk: typical double-humped shape of the vertical force can be seen in both limbs. Here, vertical force reaches a maximum of approximately 62% body weight in the forelimb and approximately 45% body weight in the hindlimb. B, Trot: typical single-humped shape of the vertical force can be seen in both limbs. Here vertical force reaches a maximum of approximately 100% body weight in the forelimb and approximately 75% body weight in the hindlimb.
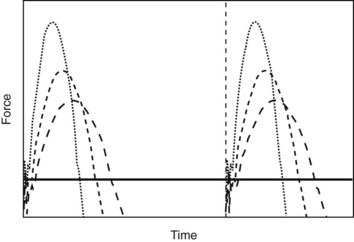
Fig. 26-4 Schematic drawing of vertical ground reaction force (y-axis) over time (x-axis) of an individual limb in a trotting horse. Each of the three graphs represents a first stance phase followed by a swing phase and a second stance phase of the same limb. Different lines indicate different speeds (long dashes, slow; short dashes, medium; dotted line, fast) and thus different stance times (for simplification purposes, stride time (indicated by the vertical line at the beginning of the second stance phase) is assumed to be constant. With increasing speed, a decrease in stance time is observed, which results in an increase in peak vertical force (the maximum force achieved during midstance) that is inversely proportional to duty factor (ratio of stance time over stride time). The black horizontal line represents the average vertical force produced by the limb, which needs to be sufficiently large to support the body of the horse against the effect of gravity (i.e., approximately 30% body weight for each individual forelimb or approximately 20% body weight for each individual hindlimb).
Fig. 26-5 Schematic drawing of the equine forelimb with the direction of the ground reaction force (GRF) vector and its moment arms around the metacarpophalangeal (MCP) joint. To prevent the limb from collapsing, the extension moment is counteracted by a flexor moment created by the digital flexor tendons (here limited to the deep digital flexor tendon) and their moment arm (MA) on the palmar aspect of the limb. As the limb comes under load, the GRF moment arm around the MCP joint increases (shaded arrow). Changes in moment arms of the flexor tendons around the MCP joint are largely determined by the size of the proximal sesamoid bones and remain relatively constant (MA tendon). Hence an increase in extensor moment results in an increase in the force in the digital flexor tendons. This holds true for static conditions, but the situation during movement is more complex.
where Fext is force of the extension moment and Fflex is force of the flexion moment. The moment arm of the digital flexor tendons is the distance from the center of rotation of the joint to the line of action of the tendons. The length of the tendon moment arm is largely determined by the size of the proximal sesamoid bones at the level of the fetlock joint and the distal sesamoid bone at the level of the DIP joint. Because the size of these bones remains constant, any change in the magnitude and/or direction of the GRF will have an effect on the force the flexor tendons experience. As the DDFT wraps around the distal sesamoid (navicular) bone, it exerts a compressive force on the bone that is proportional not only to the force the tendon experiences but also to the angle of the path of the DDFT.12,13
Impact
The foot of a galloping horse hits the ground at about 5 m/sec. On first contact with the ground the leg decelerates rapidly, which is reflected in the early increase in GRF (see Figures 26-3 and 26-4).14 This energy is dissipated by the foot sliding through and penetrating into the surface and by muscles within the limb. The forces at impact are lower than those experienced in the rest of the stride, but the load is applied very quickly, which appears to be important in eliciting musculoskeletal injury. The impact “shock” also causes the limb to vibrate at about 35 Hz, somewhat like the plucking of a violin string. This vibration is predominantly in a horizontal direction and is caused by the large amount of elastic tendon tissue contained in the equine limb and the pogo stick–like lever system. Vibration is apparent in both forelimbs and hindlimbs, but the vibration amplitude and duration are greater in the forelimbs. The vibration may, in itself, cause damage through increasing loading rate and the number of loading cycles experienced by the tendons. It also has a potent remodeling stimulus on bone and perhaps other tissues.
The magnitude of the vibration is dependent on several factors. Surfaces that allow the foot to slip at impact (or on hard surfaces, a shoe that slips at contact) dissipate the impact energy and reduce the impulse that causes the vibration. Surfaces with good damping characteristics absorb the vibration energy rapidly. This feature is different from the stiffness of a surface, and it is possible to have a surface that is relatively stiff (firm) but has good damping characteristics. The foot as the interface between the body and the ground has several built-in damping mechanisms (see earlier), but the other important damping system is the muscles. Active muscles absorb energy during small-amplitude, high-frequency oscillations. The digital flexor muscles have extremely short fibers and a large physiological cross-sectional area, which means that they can develop high forces but only over a length change of a few millimeters. This arrangement makes them ideal for absorbing the energy associated with a small-amplitude vibration.8
Impact characteristics differ among gaits, speeds, surfaces, and shoes.14-17 The absolute length of the hoof-braking period is 30 to 50 milliseconds, independent of speed,14 but is affected by the type of surface. In a comparison of all-weather waxed tracks to crushed-sand tracks, the former was found to reduce the amplitude of the shock at impact and the associated vibrations in French trotters.18
Peak Force
After initial ground contact the limb is loaded in a distoproximal manner,19 with the whole limb shortening toward the ground, largely because of further extension of the fetlock joint6 but aided by rotation and translation of other segments. This prolongs the impact time and extends the period of braking, which makes the limb an effective shock absorber.20
The peak GRF increases with the body mass of the horse. The damage a force can cause depends not only on its magnitude, but also on how quickly it is applied. Force over time is called impulse and represents the area under the force/time curve (see Figure 26-4). The shape of the force/time curve is different between forelimbs and hindlimbs and varies for different gaits (see Figure 26-3) and speeds (see Figure 26-4). Impulses are highest during gallop and increase with speed within a gait. At top speed a racehorse’s front foot is on the ground for only about 80 milliseconds or 17% of the stride, and the limb experiences a peak force of about 2.5 times body weight. This load is applied in only 40 milliseconds. The load on a hindlimb is considerably lower at about 1.5 times body weight. This difference in peak load may explain, in part, why hindlimbs experience a lower incidence of tendon and ligament injuries.
Speed is a function of stride frequency and stride length. An increase in speed can be achieved by increasing either of these factors; however, neither of these can be increased endlessly. Maximum running speed is constrained by the speed at which the limbs can be moved and by the GRF they can withstand. People sprinting bends change the duration of foot contact to spread the time over which the load is applied to keep limb force constant. Racing greyhounds do not change their foot-contact timings, and so have to withstand a 65% increase in limb forces; thus in this species limb force does not limit running speed.21 It is currently not known if limb force limits running speed in horses as in people or if horses are more like greyhounds.
It is known that individual horses adopt different locomotor strategies to achieve the same speed—for example, horses with longer limbs have lower stride frequencies than horses with shorter limbs.22 An increase in stride frequency can be achieved by reducing the time that either the foot is off the ground (protraction time) or the limb is on the ground (stance time). Protraction time accounts for approximately 80% of the stride time and remains relatively constant during gallop.23 Changes in stride frequency must be largely achieved through minimizing stance time. It has been shown in people that the forces a limb experiences increase with decreasing stance time, and it is reasonable to assume that the same is true in horses. This may suggest that horses that increase speed by reducing stance time are at higher risk of musculoskeletal injury. However, with an increased stance time comes an increase in the angle a limb sweeps through while the limb is on the ground and the body continues moving over it. This is probably related to an increase in the moments acting on musculoskeletal structures. However, the potential effect of this on musculoskeletal injury has not yet been investigated.
The tissues of the distal aspect of the limb function within a narrow safety margin; this is partly the result of minimizing distal limb mass but also a prerequisite of having tendons that function as elastic energy stores (because energy stored is a direct function of the square of the elongation of a tendon). The force acting through the limb is multiplied by the lever system of the distal limb to impose much higher forces on the bones and tendons of the distal aspect of the limb. These forces approach the mechanical capacity of these tissues, and a small increase in peak load results in a substantial reduction in the number of cycles to failure for the tissue. The relative load distribution between the individual digital flexor tendons also varies by, for example, the angle of the foot to the ground (resulting from either shoe design or the way the foot penetrates into the surface). Elevation of the heel results in a transfer of load from the DDFT to the SDFT and the SL (Figure 26-6).
Fig. 26-6 A, Calculation of mean digital flexor tendon and suspensory ligament (SL) forces in the affected (top) and contralateral (bottom) forelimb of five trotting horses before (solid line) and after (dashed line) experimentally induced unilateral superficial digital flexor (SDF) tendonitis. B, Calculation of mean digital flexor tendon and SL forces in the affected (top) and contralateral (bottom) forelimb of five trotting horses with experimentally induced unilateral SDF tendonitis before (dashed lines) and after (dotted lines) bilateral application of heel wedges. DDF, Deep digital flexor, including accessory ligament of the DDF tendon (ALDDFT); SDF, superficial digital flexor.
(From Meershoek LS, Lanovaz JL, Schamhardt HC, Clayton HM: Calculated forelimb digital flexor tendon forces in horses with experimentally induced superficial digital flexor tendinitis and the effects of application of heel wedges, Am J Vet Res 63:432, 2002.)
Number of Loading Cycles
Large volumes of high-speed exercise may exceed the fatigue life of the high-stress tendons and bones. The fatigue life of these tissues (in number of cycles to failure) depends on the peak strain (deformation) experienced; a small increment in strain results in a substantial reduction in the fatigue life of a tissue. The volume of high-speed exercise applied to a horse is therefore critical. High-speed exercise is also the most potent stimulus for eliciting changes in structural properties, so there is a trade-off between providing this stimulus and exceeding the mechanical capacity of these tissues. A galloping horse imposes about 220 loading cycles per mile (strides) on its bones and tendons at a fast gallop and about 360 strides per mile at a canter. These structures have been estimated to have a fatigue life of as little as 10,000 cycles. The relationship between speed and number of cycles to failure is of interest in the development of appropriate training programs. The time course of structural adaptations may be as long as 6 months, and there is the potential for a training program to accumulate damage (because of the exercise volume) before such protective responses occur.
What Happens to the Individual Musculoskeletal Element during Locomotion?
Foot
On contact with the ground the foot must withstand the high forces at impact. During locomotion a forelimb of a horse experiences forces of one half of body weight at a walk, approximately 1 times body weight at a trot, and up to 2.5 times body weight at a canter.
Forces act on the foot primarily in two ways: the GRF acts on the solar surface of the hoof, and tensile forces are applied by the DDFT to its insertion site on the distal phalanx. Forces acting on the foot are transferred between the distal phalanx and the hoof capsule through the laminar junction (see Figure 26-2). In effect the limb force is transferred to the distal phalanx, and it is “hung” from the hoof wall by the laminae. This is why in laminitis, with disruption of the dorsal laminae, the dorsal aspect of the distal phalanx drops. Movement of the distal phalanx and deformation of the hoof wall have secondary effects on vascularization, the whole process being termed the hoof mechanism.10
As the hoof capsule comes under load, the main force moves from the palmar or plantar aspect of the hoof dorsally to the toe,24 and the dorsal hoof capsule compresses. The heel expands during the first three quarters of the stance phase and contracts for a short time just before the foot leaves the ground. Heel expansion is greater in trot than in walk, but the timings are similar. Initially the middle phalanx rotates palmad or plantad, causing the heel, frog, and wall to deform under pressure. There is a direct relationship between hoof pressure, particularly in the frog, and heel expansion. However, heel expansion occurs even without ground contact with the frog, and there is no direct pressure from the ground acting on the sole or frog.25
The strain patterns and peak strains of the hoof capsule are complex and are influenced by numerous factors such as gait, hoof shape, shoeing, and surface and pathological conditions.10,26,27 Generally strains are lower in walk than in trot and gallop; turning increases the strain on the medial hoof quarter.
Tendons
Accurate measurement of tendon strain is a challenge, especially in live horses, and numerous in vitro and in vivo experiments using a variety of invasive and noninvasive techniques have been conducted to assess tendon strain in horses.
The time-related pattern of loading and the magnitude differ between the digital flexor tendons (see Figure 26-6) and are influenced by surface, conformation, farriery, and pathology.28-32 Tendon strain in vivo increases significantly from walk to trot for all digital flexor tendons with the exception of the ALDDFT. The highest strains are experienced by the SL (3.4% at walk, 5.8% at trot), followed by the SDFT (2.2% at walk, 4.2% at trot) and DDFT (1.2%, 1.7%). Strains in the ALDDFT and SL were significantly higher on pavement than on sand, but this was not found for the SDFT and DDFT.31 At a gallop, tendon strain can reach 12% to 16%,33 a level close to failure strain found experimentally (see Figure 68-1), suggesting that a narrow safety margin exists for tendon tissue. A similar distribution of tendon forces has been seen during landing after fences.34 Peak forces were highest in the SL, lower in the SDFT and lowest in the DDFT. Increase in fence height resulted in a substantial increase in SDFT force, whereas forces in the SL increased only slightly, and forces in the DDFT and ALDDFT remained the same. The loading pattern of the digital flexor tendons over time differs between tendons. Force in the SL increases in the first 30% of the stance phase, remains nearly constant at 30% to 70%, and decreases between 70% of stance and foot-off. Force in the DDFT and ALDDFT increases more gradually until its peak at 75% of the stance phase and decreases rapidly thereafter, whereas the SDFT starts loading at 10% of stance and reaches its peak at midstance.
Surface characteristics were related to the incidence of tendon injuries in epidemiological studies35,36 and had a significant influence on tendon load in two French trotters: when an all-weather track was compared with a crushed-sand track, the maximum force experienced by the SDFT was higher and was reached earlier in the stance phase on the crushed-sand track than on the all-weather track.37 This corresponds to differences in joint kinematics and foot-surface interaction between the two surfaces. However, more studies are necessary comparing the effect of surfaces on other tendons, bones, and joints before recommendations regarding the most suitable surface can be made.
Bones
The McIII is one of the most commonly fractured bones in racehorses. The stress and strain patterns this bone experiences during locomotion33,38,39 are complex, involving compression, shearing, bending, and twisting. Strains exceeding 3000 microstrain have been recorded for the dorsal cortex of the McIII during fast exercise, and the peak compressive strain of this bone at a speed of 16 m/sec was found to be around 4800 microstrain.40 These high strain values are thought to stimulate bone modeling, but they can also cause simultaneous bone damage. However, the peak axial load may be unlikely to cause a fracture in this bone.41 Axial stress, about 90 N/mm2, can be calculated from the measured strain values by taking into account the material properties and average cross-sectional area of the McIII.42 This corresponds to about 50% of the ultimate strength.43 It has been shown that the force required to break a bone through bending is only about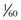 
of the force required to fracture a bone in compression.44 Therefore the bending forces are much more likely to cause overload in the McIII. Horizontally directed accelerations and hence the bending forces acting on the McIII are highest during impact, and it has been suggested that any measures interfering with this phase have an effect on the McIII stress.41 This is supported by the fact that a shorter period of hoof braking after foot contact has been shown to result in higher amplitudes and more rapid oscillation transmitted to the McIII in horses at trot than a longer period of braking.16
A more detailed description of bone loading is given in Chapter 102.
Joints
Joints are mainly subjected to compressive and shear forces. Direction and magnitude of the force follows the GRF and is influenced by joint angle and conformation of the joints and limb segments. Stress relates to the size and shape of the articular surfaces and therefore differs among joints, but also within a joint. In the metacarpophalangeal (MCP) joint, for example, the stress follows the biphasic GRF pattern during walk at most articular sites, but not the sagittal groove of the proximal phalanx, where stress has been shown to continue to rise after midstance in a majority of horses.45 This may contribute to the pathobiology of this specific area. In this joint the stress experienced by the medial part of the joint was significantly higher than the stress acting on the lateral part, which corresponds to the progression of osteoarthritic changes from medial to lateral in this joint.46
The Effects of Conformation on Equine Distal Limb Mechanics
The effect of conformation, especially with regard to the relationship among heel height, toe length, and angulation of the phalanges, is commonly discussed by veterinarians and farriers; however, scientific evidence is scarce.
Effect of Toe Length and Angle
Toe length and angle influence the point of force application and hence the moment arm of the GRF around the joints, but also the relative timing of events during the stance phase.
A change in dorsal hoof wall angle of 3.5 degrees over an 8-week shoeing interval resulted in a shifting of the point of force in a dorsal direction and an increase in the moment around the DIP joint, which leads to an increase in stress exerted by the DDFT on the navicular bone.47,48 This, however, was lower than expected from predictive calculations, and a compensatory mechanism involving a decrease in extension of the fetlock joint and hence an unloading of the DDFT has been suggested.49 An additional compensatory mechanism has been suggested in the hindlimb, where a shift of the point of force laterally has been observed in late stance, resulting in a shortening of the GRF moment arm around the DIP joint.
When the heel leaves the ground, the body weight acts at the toe, producing a long lever arm on the DIP joint and hence loading the DDFT and the navicular bone. Attempts to reduce the length of this lever arm have been made by fitting a shoe with quarter clips rather than a toe clip and a shoe designed along the lines of the four-point trim (natural balance shoe). Comparing toe clip, quarter clip, and natural balance shoes, pulling the toe back made breakover (heel off to toe off) start earlier and shortened the duration of breakover. The moment arm of the GRF on the DIP joint during breakover was reduced, but because breakover started earlier and hence at a higher GRF, the peak moment and force on the navicular bone were similar with the three shoe types.50
Effect of Mediolateral Imbalance
The horse’s limb has evolved to function in the sagittal plane, with the GRF vector ideally going through the middle of the limb column to ensure even load distribution in a mediolateral plane. Any out-of-plane conformation results in a change in direction of the GRF vector and its moment arm in relation to the musculoskeletal structure, thus resulting in their uneven loading and hence potential overloading of structures that have low safety factors. Mediolateral imbalance leads to an increase in joint pressure, as well as changes in articular contact area, as demonstrated for the DIP joint after application of medial or lateral wedges.51 Six-degree lateral or medial wedges resulted in a significant increase in joint pressure and moved the articular contact area toward the elevated side.
One aim of veterinary and farriery intervention is to ensure mediolateral balance through foot trimming or addition of extensions. The effect of such treatments on limb mechanics in sound horses and in horses with OA of the distal hock joints (bone spavin) has been demonstrated. In one study a 6-mm–thick wedge shoe was applied to alter mediolateral foot balance in sound horses of good conformation.24 This wedge moved the PZM toward the elevated side of the foot by about 5 to 10 mm. In a second study a 20-mm-wide lateral extension was applied to the front and separately to the hind feet of sound horses. These extensions had no apparent effect on the position of the PZM. This lack of an effect may demonstrate, however, that “if it ain’t broke, you can’t fix it.” In addition, on soft ground an extension sinks into the ground less than the narrow side of a shoe, creating a wedge effect. In a separate study lateral extensions and trailer shoes were applied to the hind feet of horses with OA of the distal hock joints. These horses attempted to unload the dorsomedial aspect of the distal tarsal joints by redistributing their weight to the plantarolateral aspect of the foot. The lateral extensions (20 mm wide) and trailers (20 mm long on lateral heel) are assumed to act by helping the horse to redistribute its weight in a more comfortable manner either by rotating the foot or by helping the horse bear weight on the lateral side of the foot. An alternative explanation is that the corrective farriery forces the horse to move “normally” and prevents it from unloading the painful tissues and eliciting the repair process. Both extension and trailer shoes had little consistent effect on the position of the PZM through stance or on the clinical lameness score of these horses, questioning their efficacy as a treatment technique. The Editors question the assumption that pain is focused dorsomedially.
Effect of Heel Height
It is common to change heel height through the application of heel wedges to manage orthopedic disease in horses. The effect of wedges on joint angles, tendon strains, and joint pressure has been the subject of numerous studies and the mechanical effects in the following sections have been described.
Joint Angles, Tendon Strain, and Navicular Force
Heel wedges move the PZM toward the heel and therefore reduce the moment arm of the GRF at the DIP joint and unload the DDFT. The DDFT passes around the navicular bone and exerts a compressive force on the navicular bone. When the DIP joint is flexed, the angle of tendon deviation around the bone is reduced. Angular change and a reduced force in the tendon (because it has shortened) mean that the compressive force on the bone is reduced. Force on the navicular bone is reduced nearly 24% for a 6-degree heel wedge and double that for a 21-degree wedge.12
When the heel is unloaded toward the end of stance, there is leverage on the DIP joint, the DDFT, and the navicular bone. With wedge elevation the heel is supported until later in the stride. Vertical force on the limb is reduced when forward displacement occurs, and in turn the moment on the DIP joint should be lower.12
These changes are supported by another study in horses with experimentally induced superficial digital flexor (SDF) tendonitis. After bilateral application of 6-degree heel wedges, ALDDFT and DDFT force decreased in both limbs; SDFT force stayed the same in the affected limb, but increased in the contralateral limb. These findings suggest that heel wedges may not be beneficial in horses with SDF tendonitis and in fact may contribute to the high secondary injury rate in contralateral forelimbs.34
Experiments using heel wedges have concentrated on the immediate effects of changes in heel height, but there are long-term, repetitive effects and possible compensatory mechanisms that may be important. In a study investigating foot conformation in sound horses there was a strong negative correlation between DDFT strain and navicular bone stress and the ratio of heel and toe height. With elevation of the toe, there is an increase of the GRF moment arm around the DIP joint because of movement of the PZM toward the toe. To counteract the increased extensor moment of the GRF on the DIP joint, the flexor moment has to increase accordingly, which leads to an increase in force in the DDFT. As the DDFT wraps around the navicular bone it exerts a force on the navicular bone, and any increase in DDFT force leads to an increase in the force acting on the navicular bone.13 The results of this study support the findings seen after heel wedge application as discussed earlier.
Joint Pressure and Articular Contact
Elevating the heel by 5 degrees has been shown to significantly increase DIP joint pressure, and lowering the heel had the opposite effect. Articular contact area shifted dorsally with elevation of the heel and palmarly when the heel was lowered.51 An increase in intraarticular pressure may directly cause pain, and indirectly could change both vascularity of the synovium and cartilage function, triggering a cascade of detrimental events.
Hoof Capsule
The horn of the hoof capsule is arranged in tubules, which is the ideal design to withstand high compressive forces, but which can be highly susceptible to excessive bending forces (comparable to a drinking straw, which is almost impossible to squash by compressing straight from either end but is very easy to bend). The compression strength of a material diminishes rapidly with increasing length, because the buckling limit of a material is proportional to the square of the length. This is why it is a mechanical necessity to maintain tubule length by natural wear or trimming. In horses with a collapsed or underrun heel, the tubules have started to bend once they have grown distal to the distal phalanx. This impairs hoof deformation and associated blood flow to and from the hoof. Application of thin, flexible carbon fiber patches to the medial and lateral sides of the heel is beneficial in maintaining horizontal loading of hoof tubules by preventing bending and restoring hoof deformation and blood flow to more physiological levels.52
Effect of Shoeing
Application of a Shoe
Application of a shoe changes the mass of the distal limb, alters hoof deformation, and influences foot-surface interaction.
A shoe changes the reaction of the distal limb to forces by increasing mass and changing inertia. This has numerous effects, mainly noticeable in the protraction phase of the stride.53 Of more importance with regard to injury are the effects of shoes on the stance phase of the horse, such as a slight increase in loading of the limb, slightly faster rotation of the hoof, less vertical lifting of the hoof,54 and an increase of up to 14% in force exerted on the navicular bone by the DDFT.12 Shod horses also show less heel expansion during stance and more contraction of the heel at the end of stance than unshod horses.25 There is evidence that shoes change ground contact area and load distribution.55 These and other mechanisms may account for observed changes in shock-absorbing capabilities observed with shoes,56,57 resulting in an increase of load during impact. This increase in impact, however, does not extend much beyond the distal phalanx, and changes between shod and unshod horses are minimal at the fetlock level.12
The Influence of Shoe Material
There is anecdotal evidence that some horses are “more comfortable” or “go better” in plastic or rubber shoes. This has been attributed to reduction of “jarring” after impact. Shoe grip varies among shoe types, and various techniques are commonly used to enhance shoe grip, such as studs or high-friction material such as rubber. Time and slide distance of a foot at impact are not significantly altered by shoe application regardless of the material used (steel, plastic, rubber). However, decelerating forces after impact and dynamic friction are significantly lower with plastic shoes compared with rubber or steel shoes.58 Horses may compensate for different shoe-ground interaction by altering gait to maintain a constant slip time and distance.
The Influence of Shoe Type
Egg bar shoes have been shown to have no effect on the force on the navicular bone in sound horses12 but have had a significant unloading effect in some horses with navicular disease, particularly those with a collapsed heel.59 Clinical experience is similar: egg bar shoes may be beneficial in some horses but not others. The mechanism of action is unclear. Egg bar shoes may redistribute load over a larger area of the heel, reinforce or couple the flexible palmar regions of the foot, and/or reduce heel pain. Redistribution of load to make a horse more comfortable also results in a reduced force on the navicular bone. Why egg bar shoes help some horses more than others is unclear but may relate to the exact location of pain, the type of pathology, and/or the degree of heel collapse.
Shoes with toe clips, shoes with quarter clips, and natural balance shoes were compared. Pulling the toe back made breakover (heel off to toe off) start earlier and shortened the duration of breakover. The moment arm of the GRF on the DIP joint during breakover was reduced, but because breakover started earlier and hence at a higher GRF, the peak moment and force on the navicular bone were similar in the three shoe types.50
Alterations in Mechanics with Specific Orthopedic Disorders
Changes in kinematics and kinetics are mainly pain induced and rarely pathognomonic in horses. Chapter 22 provides an overview of locomotor changes and compensatory mechanisms associated with lameness in horses and how these can be assessed objectively.
Studies on changes in mechanics with specific orthopedic disorders are rare. These studies are scientifically challenging for a variety of reasons, not the least of which is difficulty in standardizing subjects.
Mechanics of Palmar Foot Pain and Navicular Syndrome
In a study investigating the mechanics of the distal limb in normal horses and horses with palmar foot pain, there was a significant difference in the load distribution through the stride. A combination of force plate analysis, motion analysis, and radiography was used to determine the limb forces, the weight distribution under the foot, the force in the DDFT, and the compressive stress on the navicular bone during the stance phase of trot. These data show that in normal horses the force on the navicular bone rises through stance to a peak at around 85% of stance just before the heel leaves the ground.59 This force profile is caused by passive loading of the DDFT via its accessory ligament: as the DIP joint extends in late stance the tendon is stretched, increasing the force in the tendon and hence the compressive force it exerts on the navicular bone. In horses with palmar foot pain, the force on the navicular bone peaks early in stance and again just before the heel leaves the ground. The late peak is similar in magnitude in normal and diseased horses, but the early peak, present only in horses with navicular disease, results in a much higher loading rate on the bone, which may be responsible for the pathological remodeling observed in horses with the disease.8 After palmar digital analgesia the tendon force and hence the force on the navicular bone dropped in early stance and midstance.60 The observed changes were thought to be caused by the phenomena discussed in the following paragraphs.
The horse perceives general pain in the navicular or heel region rather than pain specific to the navicular bone. This pain could be the result of a variety of pathologies. The horse compensates for this pain in the heel region by landing toe first. The heel is unloaded at the beginning of stance to reduce concussion. After landing the PZM is moved dorsally, increasing the GRF moment arm on the DIP joint, hence increasing force in the DDFT and increasing the force exerted by the DDFT on the navicular bone. Palmar digital analgesia reverses this response to some extent, and the load on the navicular bone is reduced.59 These data suggest there may be a positive feedback mechanism in which navicular region pain elicits a compensatory mechanism that increases the compressive force on the navicular bone. This may explain why some horses with chronic heel pain develop radiological changes in the navicular bones. Whether such an increase in loading would actually cause navicular disease is unproven. This mechanism can also provide an explanation for the reported susceptibility of horses with a broken-back hoof-pastern axis to the development of navicular disease and the tendency of some horses with long-standing navicular disease to develop boxy, upright feet. A horse with collapsed heels will tend to exert a higher force on its navicular bones (because the DDFT is stretched further; see earlier) so it will be more susceptible to develop navicular disease. A long toe increases the moment arm on the DIP joint and thus the force on the navicular bone during toe-first landing and possibly also at breakover. Some horses that are attempting to unload their heels are presumably so successful that they will develop contracted heels and upright feet.
Changes in Mechanics in Horses with Laminitis
A change in foot mechanics is also apparent in horses with laminitis. The laminar junction is weakened, and the normal force transfer from the hoof wall to the distal phalanx via the laminar junction is disrupted. In sound horses the laminae deform elastically under load; in a laminitic horse the laminae change plastically, which, together with detachment of the laminae, results in rotation and/or sinking of the distal phalanx within the hoof capsule, which further disrupts the normal mechanical behavior of the hoof with subsequent consequences to its vascularization.
Laminitic horses land heel first, which is assumed to be to protect the painful dorsal laminae (laminar detachment occurs predominantly in the dorsal region of the foot). Laminar detachment destabilizes the distal phalanx and results in rotation and/or sinking of the distal phalanx, depending on the extent of detachment with respect to the position of the PZM. Rotation occurs when there is weakening of the laminae in the dorsal region, yet the laminae at the heel remain mechanically competent. The distal phalanx pivots about this point so that the toe moves palmad and distad following the “pull” of the DDFT. Rotation of the distal phalanx causes shortening of the DDFT and reduction of the force in the DDFT. The reduction in DDFT force results in a reduced flexor moment in the DIP joint during stance. Because the moments on the DIP joint must balance, this reduces the extensor moment created by the GRF. This reduction in moment is reflected in the PZM moving toward the heel. The dorsal laminae are unloaded and the proportion of the load transferred through the intact palmar laminae is increased.61 Rotation can thus be regarded as a self-limiting event, the magnitude (angle) of which depends on the degree of laminar detachment. If extensive laminar detachment occurs, then the forces exerted on the remaining laminae will exceed their mechanical capacity, and the distal phalanx will sink rather than rotate further.
Changes in Mechanics in Horses with Osteoarthritis of the Distal Hock Joints
Horses with OA of the distal hook joints (bone spavin) are described as having a characteristic gait. The gait is characterized by a shortened cranial phase of the stride; the limb is moved medially during the flight phase and then swung laterally just before ground impact (“stabbing”). This gait is believed to be the result of the horse attempting to reduce the load on the painful medial aspect of the tarsus. In a study comparing normal horses and horses with bone spavin and the position of the PZM in the hind feet, the PZM was found to be more plantar and lateral than in normal horses, confirming that they change their gait to unload the painful medial aspect of the tarsus.62 The Editors have observed a similar gait associated with many other sources of hindlimb pain and debate the existence of pain on only the dorsomedial aspect of the distal hook joints.
Changes in Mechanics in Horses with Superficial Digital Flexor Tendonitis
In horses with experimentally induced SDF tendonitis, trotting speed slowed and therefore forces decreased. In the affected limb, however, force in the SL decreased more than that in the SDFT and DDFT, thus changing load distribution between the flexor structures (see Figure 26-6).34 More information about the role of mechanics in the pathobiology of tendon injury is given in Chapter 68.
Conclusion
Biomechanics is an ever-changing field, the progress of which is closely linked to the evolution of new techniques and computational power. Horses do not get injured standing still, and musculoskeletal injury is strongly related to exercise. The quantification of locomotor parameters at high speed under field conditions is relatively new and will lead to more insights in the future. The horse’s musculoskeletal system is finely tuned by millions of years of evolution, and changes in one structure inevitably lead to changes in others. Understanding the complex interactions among the individual musculoskeletal structures, how they are influenced by the surface, and how these interactions vary among individual horses is a prerequisite to understanding not only the development of musculoskeletal disorders, but also how to best treat them and, even better, how to prevent them.