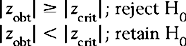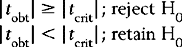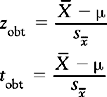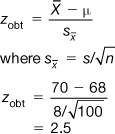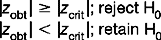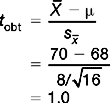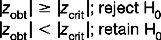Chapter Eighteen Hypothesis testing
Introduction
In the previous chapter we introduced the use of inferential statistics for estimating population parameters from sample statistics. In the case of some non-experimental research projects, such as surveys and descriptive statistics, parameter estimation is adequate for analysing the data. After all, these investigations aim at describing the characteristics of specific populations. However, other research strategies involve data collection for the purpose of testing hypotheses. Here the investigator has to establish if the data support or refute the hypotheses being investigated. The key issue is that hypotheses are generalizations addressing differences in patterns and associations in populations. Inferential statistics enables us to calculate the probability (level of significance) for asserting that what we are seeing in our sample data is generalizable to the population. This probability is related to the statistical significance of the sample data.
The aim of this chapter is to introduce the logical steps involved in hypothesis testing in quantitative research. Given that hypothesis testing is probabilistic, special attention must be paid to the possibility of making erroneous decisions, and to the implications of making such errors.
A simple illustration of hypothesis testing
One of the simplest forms of gambling is betting on the fall of a coin. Let us play a little game. We, the authors, will toss a coin. If it comes out heads (H) you will give us £1; if tails (T) we will give you £1. To make things interesting, let us have 10 tosses. The results are:
Oh dear, you seem to have lost. Never mind, we were just lucky, so send along your cheque for £10. What is that, you are a little hesitant? Are you saying that we ‘fixed’ the game? There is a systematic procedure for demonstrating the probable truth of your allegations:
The probability of calculating the truth of H0 depended on the number of tosses (n = the sample size). For instance, the probabilities of obtaining all heads with up to five tosses, according to the binomial theorem (Ch. 17), are shown in Table 18.1. The table shows that, as the sample size (n) becomes larger, the probability at which it is possible to reject H0 becomes smaller. With only a few tosses we really cannot be sure if the game is fixed or not: without sufficient information it becomes hard to reject H0 at a reasonable level of probability.
Table 18.1 Probability of obtaining all heads in coin tosses
| n (number of tosses) | p (all heads) |
|---|---|
| 1 | 0.5000 |
| 2 | 0.2500 |
| 3 | 0.1250 |
| 4 | 0.0625 |
| 5 | 0.0313 |
A question emerges: ‘What is a reasonable level of probability for rejecting H0?’ As we shall see, there are conventions for specifying these probabilities. One way to proceed, however, is to set the appropriate probability for rejecting H0 on the basis of the implications of erroneous decisions.
Obviously, any decision made on a probabilistic basis might be erroneous. Two types of elementary decision errors are identified in statistics as Type I and Type II errors. A Type I error involves mistakenly rejecting H0, while a Type II error involves mistakenly retaining H0.
In the above example, a Type I error would involve deciding that the outcome was not due to chance when in fact it was. The practical outcome of this would be to accuse the authors falsely of fixing the game. A Type II error would represent the decision that the outcome was due to chance, when in fact it was due to a ‘fix’. The practical outcome of this would be to send your hard-earned £10 to a couple of crooks. Clearly, in a situation like this, a Type II error would be more odious than a Type I error, and you would set a fairly high probability for rejecting H0. However, if you were gambling with a villain, who had a loaded revolver handy, you would tend to set a very low probability for rejecting H0. We will examine these ideas more formally in subsequent parts of this chapter.
The logic of hypothesis testing
Hypothesis testing is the process of deciding statistically whether the findings of an investigation reflect chance or real effects at a given level of probability. If the results do not represent chance effects then we say that the results are statistically significant. That is, when we say that our results are statistically significant we mean that the patterns or differences seen in the sample data are generalizable to the population.
The mathematical procedures for hypothesis testing are based on the application of probability theory and sampling, as discussed previously. Because of the probabilistic nature of the process, decision errors in hypothesis testing cannot be entirely eliminated. However, the procedures outlined in this section enable us to specify the probability level at which we can claim that the data obtained in an investigation support experimental hypotheses. This procedure is fundamental for determining the statistical significance of the data as well as being relevant to the logic of clinical decision making.
Steps in hypothesis testing
The following steps are conventionally followed in hypothesis testing:
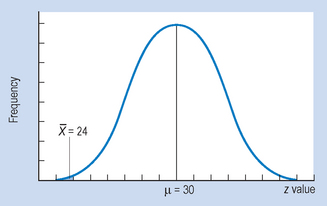
Let us look at an example. A rehabilitation therapist devises an exercise programme which is expected to reduce the time taken for people to leave hospital following orthopaedic surgery. Previous records show that the recovery time for patients has been μ = 30 days, with σ = 8 days. A sample of 64 patients are treated with the exercise programme, and their mean recovery time is found to be 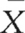 = 24 days. Do these results show that patients who had the treatment recovered significantly faster than previous patients? We can apply the steps for hypothesis testing to make our decision.
= 24 days. Do these results show that patients who had the treatment recovered significantly faster than previous patients? We can apply the steps for hypothesis testing to make our decision.
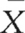 = 24, and n = 64 is in fact a random sample from the population μ = 30, σ = 8. Any difference between
= 24, and n = 64 is in fact a random sample from the population μ = 30, σ = 8. Any difference between 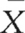 and μ can be attributed to sampling error.
and μ can be attributed to sampling error.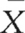 = 24 is a random sample from the population with μ = 30, σ = 8. How probable is it that this statement is true? To calculate this probability, we must generate an appropriate sampling distribution. As we have seen in Chapter 17, the sampling distribution of the mean will enable us to calculate the probability of obtaining a sample mean of
= 24 is a random sample from the population with μ = 30, σ = 8. How probable is it that this statement is true? To calculate this probability, we must generate an appropriate sampling distribution. As we have seen in Chapter 17, the sampling distribution of the mean will enable us to calculate the probability of obtaining a sample mean of 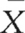 = 24 or more extreme from a population with known parameters. As shown in Figure 18.1, we can calculate the probability of drawing a sample mean of
= 24 or more extreme from a population with known parameters. As shown in Figure 18.1, we can calculate the probability of drawing a sample mean of 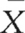 = 24 or less. Using the table of normal curves (Appendix A), as outlined previously, we find that the probability of randomly selecting a sample mean of
= 24 or less. Using the table of normal curves (Appendix A), as outlined previously, we find that the probability of randomly selecting a sample mean of 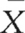 = 24 (or less) is extremely small. In terms of our table, which only shows the exact probability of up to z = 4.00, we can see that the present probability is less than 0.00003. Therefore, the probability that H0 is true is less than 0.00003.
= 24 (or less) is extremely small. In terms of our table, which only shows the exact probability of up to z = 4.00, we can see that the present probability is less than 0.00003. Therefore, the probability that H0 is true is less than 0.00003.Directional and non-directional hypotheses and corresponding critical values of statistics
In the previous example, HA was directional in that we asserted that the difference between the mean of the treated sample and the population mean was expected to be in a particular direction. If we state that there was some effect due to the dependent variable, but do not specify which way, then HA is called non-directional. In the previous example, if the investigator stated HA as ‘The exercise programme changes the time taken to recover following surgery’ then HA would have been non-directional.
In general, an alternative hypothesis is directional if it predicts a specific outcome concerning the direction of the findings by stating that one group mean will be higher or lower than the other(s). An alternative hypothesis is non-directional if it predicts a difference, without specifying which group mean is expected to be higher or lower than the others.
If we propose a directional HA, it is understood that we have reasonable information on the basis of pilot studies or previously published research for predicting the direction of the outcome. The advantage of a directional HA is that it increases the probability of rejecting H0. However, the decision of the directionality of HA must be decided before the data are collected and analysed.
Let us now examine the concept of the ‘critical’ value of a statistic. The critical value of a statistic is the value of the statistic which bounds the proportion of the sampling distribution specified by α. The critical value of the statistic is influenced by whether HA is directional or non-directional.
Figures 18.2 and 18.3 represent the sampling distributions of the mean where n is large; that is, the sampling distribution for the statistic 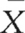 .
.

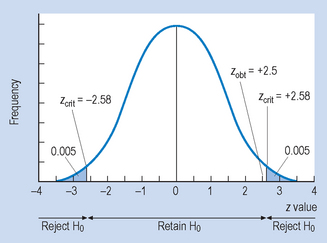
Figure 18.3 Two examples of statistical decision making with non-directional (two-tail) hypothesis, HA.
As we have seen in Chapter 17, these are the sampling distributions for 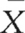 we would expect by the random selection of samples, as specified by H0. Therefore, we can estimate from the distributions the probability of selecting any sample mean,
we would expect by the random selection of samples, as specified by H0. Therefore, we can estimate from the distributions the probability of selecting any sample mean, 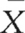 , by chance alone. The α value (the level of significance) specifies the criterion for rejecting H0. We can see that the critical value for the statistic (in this case zcrit) cuts off an area of the distribution corresponding to α (p = 0.05 or p = 0.01).
, by chance alone. The α value (the level of significance) specifies the criterion for rejecting H0. We can see that the critical value for the statistic (in this case zcrit) cuts off an area of the distribution corresponding to α (p = 0.05 or p = 0.01).
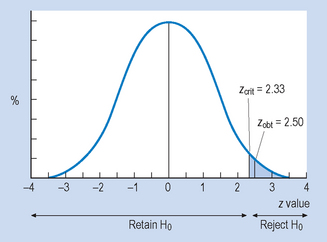
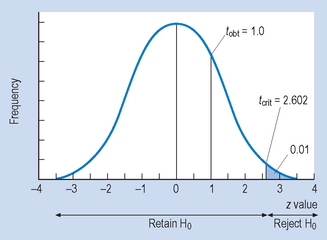
In Figure 18.2, we can see that zcrit = 1.65 (for α = 0.05) and zcrit = 2.33 (for α = 0.01). (These values are obtained from Appendix A.) Therefore, for any sample mean, 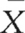 , where the transformed (z) value is greater than or equal to zcrit, we will reject H0 (that the sample mean was a random sample). However, if the absolute value of the transformed statistic is less than zcrit, then we must retain H0. Note that when α = 0.01, the zcrit is greater than when α = 0.05. Clearly, the higher the level of significance set for rejecting H0, the greater the absolute critical value of the statistic. Figure 18.2 shows statistical decision making with a directional HA, where the probabilities associated with only one of the tails of the distribution are used.
, where the transformed (z) value is greater than or equal to zcrit, we will reject H0 (that the sample mean was a random sample). However, if the absolute value of the transformed statistic is less than zcrit, then we must retain H0. Note that when α = 0.01, the zcrit is greater than when α = 0.05. Clearly, the higher the level of significance set for rejecting H0, the greater the absolute critical value of the statistic. Figure 18.2 shows statistical decision making with a directional HA, where the probabilities associated with only one of the tails of the distribution are used.
Figure 18.3 shows the critical values for z with a non-directional HA. Here, the probabilities associated with α (0.05 or 0.01) are divided between the two tails of the distribution. That is, where α = 0.05, half (0.025) goes into each tail, and where α = 0.01, half (0.005) also goes into each tail. This changes the values of zcrit, which becomes ± 1.96 or ± 2.58, respectively, as shown in Figure 18.3. Here, we reject H0 if the calculated transformed z value of 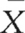 falls beyond the values of zcrit. When we compare the values of zcrit for the one-tail and two-tail decisions, we find that the critical values are greater for the two-tail decisions. This implies that it is more difficult to reject H0 if we are making two-tail decisions on the basis of a non-directional HA.
falls beyond the values of zcrit. When we compare the values of zcrit for the one-tail and two-tail decisions, we find that the critical values are greater for the two-tail decisions. This implies that it is more difficult to reject H0 if we are making two-tail decisions on the basis of a non-directional HA.
Decision rules
In general, Figures 18.2 and 18.3 illustrate the decision rules for statistical decision making for hypotheses concerning sample means. These rules are:
The same decision rules hold for the t distributions associated with the sampling distribution of the mean when n (the sample size) is small (see Ch. 17).
zobt and tobt refer to the calculated value of the statistic, based on the data:
zcrit and tcrit are the critical values of the statistic obtained from the tables in Appendices A and B. As we have seen, the values of these depend on α and the directionality of HA. | | is the symbol for modulus, implying that we should look at the absolute value of a statistic. Of course, the sign is important when considering if 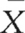 is greater or smaller than μ. However we can ignore the sign (+ or −) when making statistical decisions. In effect, the greater zobt or tobt, the more deviant or improbable the particular sample mean,
is greater or smaller than μ. However we can ignore the sign (+ or −) when making statistical decisions. In effect, the greater zobt or tobt, the more deviant or improbable the particular sample mean, 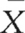 , is under the sampling distribution specified by H0.
, is under the sampling distribution specified by H0.
Statistical decisions with single sample means
The following examples illustrate the use of statistical decision making concerning a single sample mean, 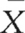 . Such decisions are relevant when our data consist of a single sample and we are to decide if the
. Such decisions are relevant when our data consist of a single sample and we are to decide if the 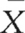 of the sample is significantly different to a given population, with a mean of μ.
of the sample is significantly different to a given population, with a mean of μ.
A statistical test is a procedure appropriate for making decisions concerning the significance of the data. The z test and the t test are procedures appropriate for making decisions concerning the probability that sample means refiect population differences. (As shown in Ch. 19, there is a variety of statistical tests available for hypothesis testing.)
Example 1
A researcher hypothesizes that males now weigh more than in previous years. To investigate this hypothesis he randomly selects 100 adult males and records their weights. The measurements for the sample have a mean of 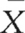 = 70 kg. In a census taken several years ago, the mean weight of males was μ = 68 kg, with a standard deviation of 8 kg.
= 70 kg. In a census taken several years ago, the mean weight of males was μ = 68 kg, with a standard deviation of 8 kg.
Example 2
A researcher hypothesized that men today have different weights (either more or less) than in previous years (assume the same information as for Example 1).
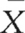 = 70 is not a random sample from population μ = 68.
= 70 is not a random sample from population μ = 68.Example 3
The previous two examples involved sample sizes of n > 30. However, as we saw in Chapter 17, if n < 30, the distribution of sample means is not a normal, but a t distribution. This point must be taken into account when we calculate the probability of H0 being true. That is, for small samples, we use the t test to evaluate the significance of our data.
Assume exactly the same information as in Example 1, except that sample size is n = 16.
Conclusion
The above examples demonstrate the following points about statistical decision making:
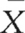 were the same, where n was small we had to retain H0. Also, when n is small, (n < 30), we must use the t test to analyse the significance of our sample mean being different.
were the same, where n was small we had to retain H0. Also, when n is small, (n < 30), we must use the t test to analyse the significance of our sample mean being different.Errors in inference
When we say our results are statistically significant, we are making the inference that the results for our sample are true for the population. It should be evident from the previous discussion that statistical decision making can result in incorrect decisions. There are two main types of inferential error: Type I and Type II.
A Type I error occurs when we mistakenly reject H0; that is, when we claim that our experimental hypothesis was supported when it is, in fact, false. The probability of a Type I error occurring is less than or equal to α. For instance, in the previous Example 1 we set α = 0.01. The probability of making a Type I error is less than or equal to 0.01; the chances are equal to or less than 1/100 that our decision in rejecting H0 was mistaken. Therefore, the smaller α, the less the chance of making a Type I error. We can set α as low as possible, but by convention it must be less than or equal to 0.05.
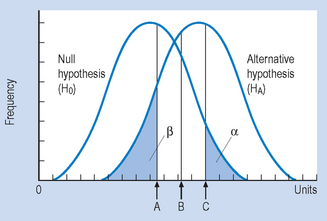
A Type II error occurs when we mistakenly retain H0; that is, when we falsely conclude that the experimental hypothesis was not supported by our data. The probability of a Type II error occurring is denoted by β (beta). In Example 3 we retained H0, perhaps falsely. If n was larger, we might well have rejected H0, as in Example 1. Type I errors represent a ‘false alarm’ and Type II errors represent a ‘miss’. Table 18.2 illustrates this.
| Reality | Decision: reject H0 | Decision: retain H0 |
|---|---|---|
| H0 correct (no difference or effect) | ‘False alarm’ Type I error | Correct decision |
| H0 incorrect (real difference or effect) | Correct decision | ‘Miss’ Type II error |
Table 18.2 illustrates that, if we reject H0, we are making either a correct decision or a Type I error. If we retain H0, we are making either a correct decision or a Type II error. While we cannot, in principle, eliminate these from scientific decision making, we can take steps to minimize their occurrence.
We minimize the occurrence of Type I error by setting an acceptable level for α. In scientific research, editors of most scientific journals require that α should be set at 0.05 or less. This convention helps to reduce false alarms to a rate of less than 1/20. Replication of the findings by other independent investigators provides important evidence that the original decision to reject H0 was correct.
How do we minimize the probability of Type II error?
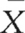 , either by increasing accuracy (Ch. 12) or by using samples that are not highly variable for the measurement producing the data).
, either by increasing accuracy (Ch. 12) or by using samples that are not highly variable for the measurement producing the data).Summary
The problem addressed in the previous two chapters was that, although our hypotheses are general statements concerning populations, the evidence for verifying or supporting our hypotheses is based on sample data. We solve this problem through the use of inferential statistics.
It was argued in this chapter that, once the sample data have been collected and summarized, the investigator must analyse the findings to demonstrate their statistical significance. Significant results for an investigation mean that differences or changes demonstrated were real, rather than just the outcome of random sampling error.
The general steps in using tests of significance were explained, and several illustrative examples using the z and t tests for single sample designs were presented. A critical value is set for the statistic (in this case zcrit, tcrit) as specified by α. If the magnitude of the obtained value of the statistic (zobt, tobt) exceeds the critical value, H0 is rejected. In this case, the investigator concludes that the data supported the differences predicted by the alternative hypothesis (at the level of significance specified by α). However, if the obtained value of the statistic is calculated to be less than the critical value, then the investigator must conclude that the data did not support the hypothesis. It was noted that following these steps does not guarantee the absolute truth of decisions made about the rejection or acceptance of the alternative hypotheses, but rather specifies the probability of the decisions being correct.
Two types of erroneous decisions were specified, Type I and Type II errors. A Type I error involves falsely concluding that differences or changes found in a study were real, that is, concluding that the data supported a hypothesis which is, in fact, false. A Type II error involves falsely concluding that no differences or changes exist, that is, concluding that the data did not support a hypothesis which is, in fact, true. It was demonstrated that the probability of these errors depends on factors such as the size of n, the directionality of HA and the variability of the data.
The procedures of hypothesis testing and error were related to the logic of clinical decision making. The probabilities (α and β) of making Type I and Type II errors are interrelated. In this way, both researchers and clinicians must take into account the implications of possible error when setting levels of significance for interpreting the data.
Self-assessment
Explain the meaning of the following terms: