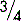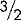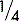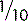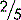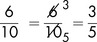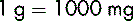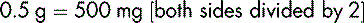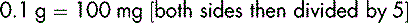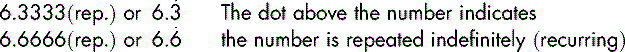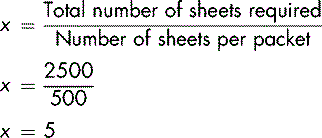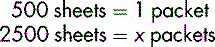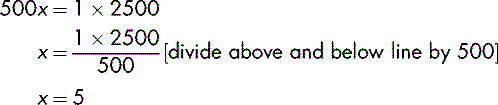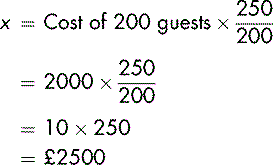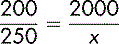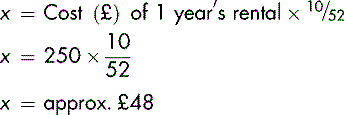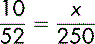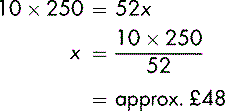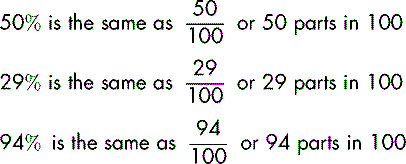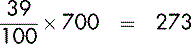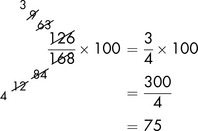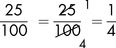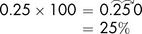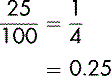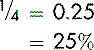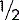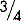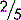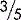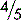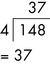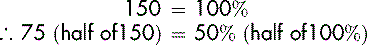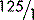CHAPTER 2 Arithmetic
Numerical skills
Numbers are an essential part of everyday life. When shopping at the supermarket for milk or fruit juice, for example, how do we know the best value for money between containers of different volumes? In order to accurately calculate drug doses and interpret data in healthcare situations, it is necessary to have certain arithmetical skills. On most occasions, the skills required are not complex; in fact, they are relatively straightforward. The skills routinely needed, either singly or in combination, are as follows:
Basic arithmetical principles
Numbers
Expressing figures
When undertaking any type of calculation, there may be times when you need to express a number in a way that will assist you. Take any number, let’s say 6.
The figure 6 can be expressed as 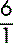 without altering the fact that it is 6.
without altering the fact that it is 6.
The figure 6 can also be expressed as 6.000 without altering the fact that it is 6. Any number of zeros can be placed after the decimal point; the number will still be valued as 6.
Great care is needed when working with very large numbers (e.g. 100 000; 250 000). It is no longer common to see in print the use of commas to signify thousands (e.g. 100,000; 250,000). It is advisable, however, to use commas when working on paper to ensure you have the right number of zeros.
Explaining fractions and decimals
The word fraction means a ‘fragment of something’.
The word decimal means ‘based on the number ten’.
Fractions may be expressed in two ways:
‘Fractions’ and ‘decimals’ are two ways of expressing a part of something. There will of course be times when the fraction or the decimal will be added to a whole number, e.g. 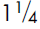 , 1.25.
, 1.25.
Fractions
‘Fractions’ are commonly used in everyday life, e.g.,
but are less often used for precise measurement.
A fraction for our purposes is formed when a number is placed above another number and the two numbers are separated by a dividing line, e.g.,
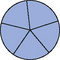
The number above the line is known as the numerator; the number below the line is the denominator. If the two numbers are the same, they will cancel each other out to become one. So,
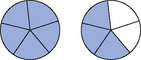
If the number above the line is less than the number below the line, the fraction is always less than one. So,
If the number above the line is more than the number below the line, the fraction must be more than one. So,
Decimals
‘Decimals’ are used in the metric system (see p. 10) and are measured in tenths, e.g.,
The decimal point is placed before the decimal fraction.
Quantities that are less than one should normally be written as a whole number of the next unit down, e.g.,
Never start a figure with a decimal point. For example, always write 0.6 and not .6. In this case, no doubt you can detect the decimal point but there may be times when the ‘decimal point’ is a blob of ink on the page!
When a fraction is expressed in decimal form:
These figures can be illustrated on a scale, as in Fig. 2.1.
Simplifying fractions (cancelling down)
When using fractions, it is always best to simplify them as far as possible, since it is easier (and safer) to work with smaller figures than with bigger ones. For example, 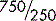 could be immediately simplified by removing the zeros (dividing by 10) to give
could be immediately simplified by removing the zeros (dividing by 10) to give 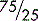 , making sure of course to delete the same number of zeros above and below the line. The fraction could then be simplified by dividing the numbers above and below the line by 25 (or in two stages by 5) to give
, making sure of course to delete the same number of zeros above and below the line. The fraction could then be simplified by dividing the numbers above and below the line by 25 (or in two stages by 5) to give  . Whatever you do above the line, you must do the same below the line. Also, simplifying a fraction does not change its value.
. Whatever you do above the line, you must do the same below the line. Also, simplifying a fraction does not change its value. 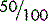 (fifty over a hundred) has exactly the same value as ½ (one over two).
(fifty over a hundred) has exactly the same value as ½ (one over two).
Some exercises are given throughout the next piece of text. Answers are on pp. 193–194.
Exercise 2.1
Here are some fractions for you to simplify:
Taking another example of a calculation which involves a fraction,
The 15 is to be divided by the 20. Another way of putting this is to say ‘20 into 15’. The result is then to be multiplied by 2.
However, it could be made easier if we were to simplify this fraction first by saying
It does not matter which of these options you use or in what order. The 15 and the 1 cannot be further simplified.
Let’s start by cancelling above and directly below the line. Both the 15 and the 20 can be divided by 5, so
Then we can simplify again by cancelling above and diagonally below the line. Both the 2 and the 4 can be divided by 2, so
Changing fractions to decimals
At times, it may be necessary to change your answer from a fraction to a decimal, e.g. prior to drawing up a volume of drug into a syringe. To convert a fraction to a decimal, divide the top number (numerator) by the bottom number (denominator).
Changing decimals to fractions
As part of the process of working out a drug calculation, you will at times want to change a decimal into a fraction.
Manipulation of numbers
When you have a fraction, for example 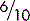 , you can divide the figure above the line and the figure below the line by the same number without fundamentally altering the fraction. Since both 6 and 10 are divisible by 2,
, you can divide the figure above the line and the figure below the line by the same number without fundamentally altering the fraction. Since both 6 and 10 are divisible by 2,
The fraction 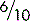 has been simplified, but the relationship between the two figures has not changed.
has been simplified, but the relationship between the two figures has not changed.
If the fraction is made up of numbers that contain a decimal point, such as 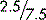 , it is acceptable to move the decimal points, provided you move them the same number of places in the same direction, above the line and below the line. It is always better to create a whole number wherever possible anyway. This can only ever be done by moving the decimal point to the right. So, to take the example of
, it is acceptable to move the decimal points, provided you move them the same number of places in the same direction, above the line and below the line. It is always better to create a whole number wherever possible anyway. This can only ever be done by moving the decimal point to the right. So, to take the example of 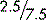 , if we move both points one place to the right (multiplying by 10), we get
, if we move both points one place to the right (multiplying by 10), we get
If you want to change one side of an equation you must do exactly the same to the other side, e.g.,
Sometimes you arrive at an answer that you cannot finish because the last digit repeats itself, e.g.:
Simple proportion
‘Proportion’ means the relation of one thing to another in magnitude. In arithmetic, it is referred to as simple proportion.
For example, you need 2500 sheets of photocopying paper, which is supplied in packets of 500 sheets.
From the above information, it is clear that more than one packet is required.
There is a direct numerical (proportional) relationship between the number of sheets required and the number of packets required. This can be expressed as a simple equation. If x is the number of packets required:
The proportions of sheets and packets will be equal:
Cross multiply (i.e. top left x bottom right = top right x bottom left)
A more complex example: you are organising a fundraising party. 250 people wish to attend. Your budget indicates that 200 guests would cost £2000. You need to know what it would cost to cater for 250 people.
Since 200 guests cost £2000 and more than 200 guests will attend, the cost will therefore be more than £2000.
There is a direct numerical (proportional) relationship between the cost of 200 guests and the cost of 250 guests. This can be expressed as a simple equation. If x is the cost (£) of 250 guests:
Or, because the proportions of guests and costs will be equal:
In the previous examples, we wanted to find quantities greater than the basic number given (one packet of paper in the first example and £2000 in the second). Now we will apply the same approach to find a quantity that is less than the basic number given.
The cost of renting an audio/visual system is £250 a year. You want to work out the cost for a 10-week period.
The cost for a 10-week period will be less than £250 since £250 is the cost for 52 weeks (one year). If x is the cost of renting for a 10-week period:
Or, because the proportions of weeks and costs will be equal:
Simple proportion is the basis from which the formula used to calculate a drug dose is derived (see p. 46).
Percentages
A percentage is written as 50%, 29%, 94%, etc. The term percentage means ‘parts per 100’ and for the purpose of a calculation can be expressed as the number preceding the % sign divided by 100, i.e. its value expressed in hundredths. So,
If 50% of a group of workers carry a packed lunch, that means 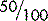 do so, which is half the group. We do not know the size of the group but we know that half of them carry a packed lunch.
do so, which is half the group. We do not know the size of the group but we know that half of them carry a packed lunch.
To take another example, if 39% out of a group of 700 patients were said to be in favour of open visiting, the actual number of patients in favour could be calculated as follows:
That means that 273 patients are said to be in favour of open visiting.
As a final example, you know that out of a class of 168 students, 126 carry a mobile phone. That may be expressed as 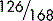 . To obtain the percentage who carry a mobile phone,
. To obtain the percentage who carry a mobile phone, 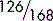 must be multiplied by 100:
must be multiplied by 100:
75% of the class carry a mobile phone.
What percentage do not carry a mobile phone?
Since 75% carry a mobile phone, the remainder don’t carry a mobile phone which is 100 – 75 = 25% don’t carry a mobile phone.
The excessive consumption of alcohol is a major public health problem and a cause of much personal ill health and misery. Guidelines have been issued on safe levels of drinking for men and women.
These levels are 2–3 units per day for women and 3–4 units per day for men. One unit is equivalent to 10 mL ethanol (ethyl alcohol).
The alcoholic strength of common drinks is as follows:
Percentages, fractions and decimals
We have already worked out how to change fractions to decimals (p. 18) and how to change decimals to fractions (p. 19). Let us now look at how to change fractions or decimals to percentages and also changing percentages to fractions and decimals.
Changing fractions to percentages
In order to change a fraction to a percentage, we multiply the fraction by 100.
Changing percentages to fractions
In order to change a percentage to a fraction, we divide the number by 100.
Changing decimals to percentages
In order to change a decimal to a percentage, we multiply the decimal by 100.
Changing percentages to decimals
In order to change a percentage to a decimal, we divide by 100.
What is 25% expressed as a decimal?
To convert fractions and decimals to percentages, we multiply by 100.
To convert percentages to fractions and decimals, we divide by 100.
Calculating percentages
We may require to calculate the percentage of a particular quantity, e.g.:
We know that 148 is the total number or in other words 100% and we need to calculate 25% of this number.
Exercise 2.9
We may also require to calculate what percentage is one number of another number, e.g., If a salesman needs to sell 150 IPods and in the first week he sells 75, what percentage has he sold?
We know that 150 is the total number or in other words 100% and we need to calculate what percentage of this is 75.
Summary
There are a number of ways of working out arithmetical problems. It does not matter a bit which method you use; use the one you are most comfortable with. What does matter is that your method helps you reach the right answer every time.
Arithmetic is an exact science. A careless arithmetical slip could have disastrous consequences. The secret is to take your time and stick to the rules. Because of their critical importance, the key points highlighted in this chapter are listed below.
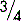 is less than
is less than 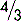
If you have forgotten your multiplication tables, now is the time to brush them up. Leave your calculator aside and pull out a piece of paper and a pencil. With guidance, many students succeed in carrying out quite intricate manoeuvres when calculating drug dosages. What often lets them down is whether or not they know ‘2 twos are 4; 2 threes are 6; 2 fours are 8’, etc. No amount of training in drug calculations will suffice unless these basic skills are learned and practised.
The next chapter describes how to do a drug calculation, where arithmetical skills will be brought to bear on this vitally important aspect of patient care.
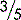 , often simply referred to as a ‘fraction’)
, often simply referred to as a ‘fraction’)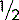 the class
the class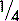 of an apple
of an apple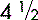 working days (whole number plus a fraction)
working days (whole number plus a fraction)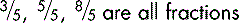
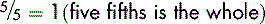
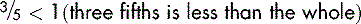


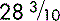 g)
g)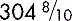 mm)
mm)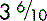 kg)
kg)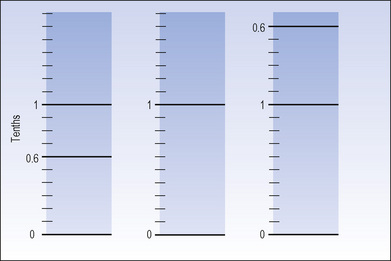
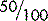
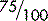
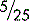
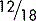
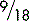
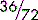

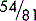


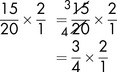
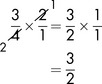
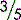 is the same as saying 3 is to be divided by 5. This may be represented as
is the same as saying 3 is to be divided by 5. This may be represented as