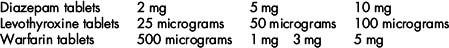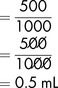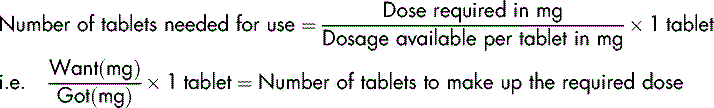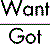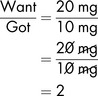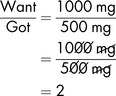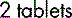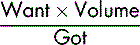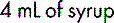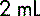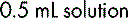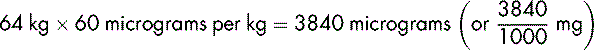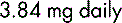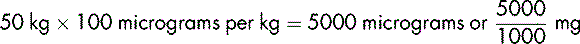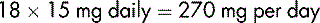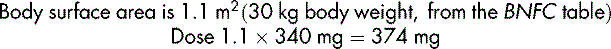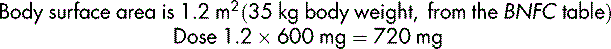CHAPTER 3 Drug calculations explained
Introduction
Having studied the theoretical components of a drug calculation, guidance is now given in their application to clinical practice.
The methods of making a calculation are considered first followed by a demonstration of how to calculate both oral and other non-parenteral doses, and parenteral doses.
The principles of how to do a drug calculation are the same whether for an adult or for a child and are considered in this chapter. Chapters 4, 5 and 6 include examples mainly for adults; Chapter 8 deals specifically with calculating in paediatrics. Ample opportunity is given to practise a range of examples which are likely to be met in the clinical area.
The examples used to illustrate the calculation methods in this text have been chosen widely to give a cross-section of current practice. It is important to note the following:
Relating details on the label to the prescription
Every time (except in an extreme emergency) a medicine is to be administered, no matter who is involved, there is a recognised procedure to be followed. The steps of this process are:
In this way, the details on the one are being compared with the details on the other and thus it can be established whether the correct strength (or combination of strengths) of preparation has been selected and whether a calculation is required.
Particular points to note when examining the details on the label and starting to work out what the patient will be given are as follows:
Select the strength(s) which will result in the patient receiving the correct dose with the minimum number of tablets
Is a calculation necessary?
Prior to the administration of a medicine, it is always important to understand fully how the information on the label of the medicine container relates to the prescription. In some cases, an actual calculation may not be necessary. In such situations, there is nevertheless always the need to correctly correlate (and understand) the quantitative information on both the prescription and the label on the medicine. Although you may find that a calculation of the dose the patient is to receive is not required, you must fully appreciate the numbers involved.
In deciding whether or not there is a need to make a calculation, the following steps should be taken prior to administering the medicine:
It is reassuring to know too that, wherever possible, the pharmacist will supply the medicine in the most appropriate form, thus reducing the need for a calculation.
If the strength of the available product exactly matches the prescribed dose, there is no need to make a calculation. The level of calculation (see p. 42) may therefore be classed as Level 0. The examples that follow are given to illustrate four situations where no calculation is required.
Where a calculation is required
Decide on a method for making the calculation with which you are comfortable (see pp. 43–50).
Medicine label
In this example, since the dose prescribed is less than the amount available, the answer must be less than 2 mL.
“As a professional, you are personally accountable for actions and omissions in your practice………….” (NMC 2008b)
With experience, you will find that it is unnecessary to go painstakingly through the steps outlined above prior to each medicine administration since, with practice, they will come naturally.
It is of the utmost importance that the principles of the calculation involved are fully understood and upheld at all times. The principles of the metric system and arithmetic are discussed in Chapters 1 and 2.
Levels of calculation
Most calculations may be considered to be at one of four levels. These levels are based on the complexity of the arithmetic and the risk involved. The more complex the calculation, the greater the risk of a drug error occurring. The concept of levels, as outlined below, has been designed by the authors, not as a rigid structure but to enable the demonstrations and exercises to be presented in a logical way, from simple to complex. The levels are:
By far the majority of calculations are at Levels I and II. Whatever the level of the calculation, care is essential. It may be necessary to slow down, to check your answer and to ask a colleague to make an independent calculation, if possible by another method, so that you are quite certain before proceeding. Calculation errors can be prevented by independent cross-checking especially in departments such as paediatrics, care of the elderly, oncology and critical care (Cohen 2007). Indeed, this may be a stipulated requirement in these areas. Normally, such action is not needed but, when it is required, it should be considered as a safe and sensible precaution and in no sense a sign of inadequacy or cause for embarrassment.
Methods used to calculate drug doses
All drug calculations are based on a clear understanding of arithmetic and a sound working knowledge of the metric system.
Two possible approaches may be used when making a calculation; the method used is often a matter of personal choice. It is important to use a method with which you are comfortable. Both methods described below can be used for all levels of calculations (see p. 42) and one method can be used to check the other.
Method 1: using the given information
This method does not require the use of a formula but is based on using the information regarding the dose of the drug on the prescription and the strength of the drug as given by the label on the medicine container. It does require a logical, stepwise approach. A number of examples of the use of this method are given below. Examples drawn from clinical practice are given in Chapters 4, 5 and 8.
In most cases, drug calculations pose the same question for the nurse, i.e. how to obtain the dose prescribed from the particular dosage form (tablet, capsule, liquid) in the strength available.
In many cases, the required calculation can be carried out mentally, but it is important to understand the principles involved since these form the basis of more complex calculations.
Example 3.5
The number of tablets needed to make up the dose is calculated by comparing the dose prescribed (i.e. 20 mg) with the strength of the available tablet (i.e. 10 mg). This can be expressed simply, as a fraction:
The prescribed dose is contained in 2 tablets.
i.e. The patient would be given:
Example 3.6
Again, a comparison is made between the dose prescribed (1 g) and the strength of the available tablet (500 mg). Each strength must be expressed in the same units, in this case milligrams, when making the calculation.
So, as 1 g = 1000 mg, the comparison is expressed as a fraction:
The prescribed dose is contained in 2 tablets.
i.e. The patient would be given:
Example 3.7
In this example, and examples 3.8 and 3.9, the medicine available is in the form of a liquid and it is necessary to take this into account when making the calculation.
In order to make a comparison between the prescribed dose and the strength of the available product, it is useful to begin by calculating the amount of drug contained in 1 mL (of syrup).
So, if 100 mg is contained in 1 mL, then there must be 400 mg in 4 mL
The prescribed dose is contained in 4 mL of syrup
Example 3.8
This example involves the use of micrograms.
To make the comparison, first calculate the amount of drug contained in 1 mL of liquid.
If there are 7 micrograms in 1 mL then there must be 14 micrograms in 2 mL
The prescribed dose is contained in 2 mL
Example 3.9
The drug is available as a 1 in 1000 solution. This is the same as saying that 1 gram of the drug is contained in 1000 mL of solution, i.e.
Dividing by 1000 to give mg/mL,
Converting 1 mg to micrograms,
The volume required for the prescribed dose (in mL) is obtained by making a comparison between the dose required and the strength of available product:
The prescribed dose is contained in 0.5 mL of the available solution.
Method 2: using the given information in a formula
The second approach to drug calculations is based on the use of a formula which is based on proportion (see pp. 20–22). Essentially, this method is similar to Method 1 but it may be preferred because of ease of use.
If the required dose is a simple multiple of the strength of the dosage form (as in Examples 3.10 and 3.11), there is no need to use a formula. The required calculation can be done mentally, although a formula may be used if preferred. Again the approach is essentially a comparison between the dose required (Want) and the strength of the available product (Got).
As an aide memoire, this can be expressed as:
Using the aide memoire for the same examples as Method 1:
Example 3.11
The prescribed dose is contained in 2 tablets.
In the case of a liquid medicine (as in Examples 3.12, 3.13 and 3.14), as well as the strength required being divided by the strength available, the strength of the available product must be expressed within a given volume (Volume).
Example 3.12
This example involves the use of a liquid medicine and therefore it is necessary to take this into account in the calculation. The formula now includes the volume of product containing the dosage available.
The prescribed dose is contained in 4 mL of syrup.
Example 3.13
This example involves the use of micrograms.
Applying the formula, with micrograms replacing mg as the units to be used:
The prescribed dose is contained in 2 mL.
Example 3.14
This example again involves the use of micrograms but the route of administration is by injection. The fact that this is a parenteral medicine does not affect the method used to calculate the dose.
Since the strength of the solution is expressed as ‘1 in 1000’ it is necessary to convert this into micrograms per 1 mL in order that the formula can be applied.
1 in 1000 is the same as saying 1 g of drug is contained in 1000 mL of solution, i.e.
Dividing by 1000 to give mg/mL,
The prescribed dose is contained in 0.5 mL solution.
Wright (2008a, 2008b) discusses the different methods in common use. The advantages and disadvantages of each calculation method used here are summarised in Table 3.1.
Table 3.1 Advantages and disadvantages of two methods of calculating doses
| Method 1: Using given information | Method 2: Using given information in a formula |
|---|---|
| Advantages | Advantages |
| Logical and stepwise | Easy to apply in busy working situation |
| Disadvantages | Disadvantages |
| More time-consuming than formula method | Incorrect figures may be inserted into the formula, leading to errors |
| A number of lines of working could introduce errors | May lead to complacency and lack of understanding of basic principles |
| Nurses may be put off by the idea of a formula |
Either method may be used for any calculation. Calculating doses of solid medicines such as tablets and capsules can often be done using Method 1. Method 2 is especially useful when working out doses of liquid medicines, either oral or injectable.
Drug doses based on body weight
Drug doses based on body weight (adults)
A number of drugs are given in doses which are calculated according to body weight. This method of dosage determination has advantages over more empirical (from experience) methods. Where the drug has a potential to damage normal tissues, e.g. cytotoxic drugs, a method based on body surface area is often used (see pp. 51–54).
Drug doses based on body weight (children)
This method of dosage determination is widely used but it has disadvantages in some situations. Young children have a high metabolic rate and may require higher doses than those determined by a body weight calculation. Obese children (determined according to body mass index (BMI)) may be given too high a dose using body weight as a basis. Where the drug has a potential to damage normal tissues, e.g. cytotoxic drugs, a method based on body surface area is often used (see p. 54). Calculations based on body weight of a child are carried out as shown above for adults.
Drug doses based on body surface area
Methods of determination of body surface area
Most physical measurements required in clinical practice can be readily obtained by simple procedures. However, body surface area (BSA) determination presents obvious practical problems. In 1916, Du Bois and Du Bois described a formula from which the BSA of a patient would be determined in square metres (m2) using the patient’s height (in centimetres (cm)) and weight (in kilograms (kg)). Since the publication of the formula, there has been much debate about the accuracy of the Du Bois and Du Bois method. Other workers have proposed ‘improved’ methods (Haycock et al 1978, Mosteller 1987, Wang et al 1992) of BSA determination.
In the following examples, a number of options are given for BSA determination. In practice, local protocols should be adhered to.
Drug doses based on body surface area (adult)
Body surface area estimates are a more accurate basis on which to calculate drug doses for both adults and children, since BSA is a better indicator of metabolic processes than body weight. Body surface areas may be determined by a nomogram, by reference to tables or by the use of a formula (not discussed here).
A nomogram is a chart which relates body weight and height to body surface area in square metres (m2). A nomogram for adults is used (Fig. 3.1).

Figure 3.1 Nomogram for adults. [As Fig. 19.4, p. 389, Pharmacology and medicines management for nurses 4E]
If the patient’s weight and height are known, the patient’s surface area can be determined. A ruler is placed across the nomogram joining the patient’s height with the patient’s weight. Where the ruler crosses the central scale, the patient’s BSA is given.
Example 3.19
Dose of doxorubicin prescribed is 60 mg/m2
The required dose should normally be prepared in a controlled environment in the pharmacy and presented in a ready-to-use form.
Taking the last example, doxorubicin injection is available as 2 mg in 1 mL solution in 100 mL vials, i.e. each vial contains:
The dose required according to BSA is 96 mg.
The required dose is contained in 48 mL of the injection solution.
The determination of a dose for an adult patient is normally straightforward. However, account must be taken of key clinical factors including liver disease or renal impairment.
Drug doses based on body surface area (children)
Children and especially neonates have less well developed pathways of metabolism and excretion of drugs than adults. The doses of many antineoplastic and immunosuppressant drugs administered to children are based on the patient’s BSA, which is generally felt to be a more accurate indicator of metabolism than body weight or age. It is essential to reduce the likelihood of toxicity to normal tissues when administering antineoplastic and immunosuppressant drugs. Dosage calculations based on BSA help to achieve this objective.
The BNF for Children (BNFC) (BMA and RPSGB 2009) gives detailed guidance on prescribing for children including the use of body surface area. It is important to have an appreciation of scale in all calculations, especially when dealing with small doses for neonates and children. In order to illustrate this, a theoretical example is offered:
A dose of 500 mg in a 70 kg man is equivalent to approximately 7 mg per kg. The same dose given to a premature baby weighing 700 g is equivalent to approximately 700 mg/kg.
The BNFC includes tables linking weight to BSA using the Boyd equation. The values for BSA may be used to calculate doses. Height is not required but it is emphasised that the body weight should always be the current value. A nomogram may also be used.
Example 3.21
A dose of mycophenolate mofetil of 600 mg/m2 twice daily is prescribed.
When calculating for neonates or young children, the doses may be very small and rounding up or down may not be appropriate as this may result in an overdose or underdose. In these cases, the exact dose must be given which may require special (extemporaneous) preparations to be made by pharmacy.
The BNFC makes many references to the use of local protocols in chemotherapy regimes. The reader may wish to access these protocols in order to gain insights into current clinical practice.
Dilution of solutions
There are occasions when a concentrated solution of a medicinal product must be diluted before use. In order to avoid calculation errors and possible contamination, it is preferable to use a ready-prepared solution of the required strength rather than make a dilution in the clinical area. It is recognised, however, that this may not always be possible.
Dilution of solutions for topical application may be required in a few instances. It is quite common for parenteral products to be diluted to a specific concentration before use. Some injections must be reconstituted and then diluted before use.
Use of calculators
Calculators should only be used to check the answer to a calculation or for making complex calculations. They may improve accuracy but they do not eliminate the need for independent practitioner review of calculations (Cohen 2007).
Nurses need not only to be fully competent in carrying out calculations but also understand the underlying principles they are using. The use of calculators to determine the volume or quantity of a medicine ‘should not act as a substitute for arithmetical knowledge and skill’ (NMC 2008a).
Over-reliance on a calculator can create a false sense of security. It should be remembered that the calculator will work on whatever figures are keyed in. If a mistake is made with a digit or the wrong sequence is entered, clearly the answer will be incorrect. Greater confidence will be reached in knowing you are able to calculate independently whether or not a calculator is available.
Drug calculations in perspective
The need to avoid errors associated with calculations is every bit as important as preventing errors in medicine administration from other causes (Downie et al 2008). Clearly, it is essential that the patient is given the intended dose on every occasion. Those who have difficulties with calculations have a professional responsibility to address the problem by seeking help, practising repeatedly until competent and, perhaps more than anything, developing a willingness to be up front about any difficulties. There is no substitute for being observant at all times. Attention to detail is vital.
It is neither helpful nor necessary for anyone teaching this subject to create a climate of fear about drug calculations. Increasingly, medicines are being dispensed in unit doses, which may reduce the need for a calculation to be made in the clinical area. Therein lies the danger of deskilling nurses in this field, with resultant problems when a complex calculation arises. Overcoming the fears that surround calculations is as much to do with keeping the subject in perspective by providing realistic examples to practise, by not making the subject unnecessarily complicated and by instilling confidence. Those who already have mastery of the subject may be used to assist those who have not. Indeed, nurses and nursing students may learn more effectively from their peers than in a more formal setting. For guidance on advanced drug calculations, the input of experienced nurse practitioners can be invaluable.
Safety in the administration of medicines requires a sound understanding of how to make a calculation where it is needed. There is no place for rote learning. Calculating the dose of a medicine is an exact science; the answer is either right or it is wrong. Everyone knows which of these it must be.
BMA (British Medical Association) and RPSGB (Royal Pharmaceutical Society of Great Britain). British National Formulary for Children (BNFC). London: BMJ Group and RPS Publishing, 2009.
Cohen M.R., editor. Medication errors, second ed, Washington, D.C: American Pharmacists Association, 2007.
Downie G., Mackenzie J., Williams A. Pharmacology and medicines management for nurses, fourth ed, Edinburgh: Churchill Livingstone; 2008:73-77.
Haycock G.B., Schwartz G.J., Wisotsky D.H. Geometric method for measuring BSA: a height/weight formula validated in infants, children and adults. J. Paediatr.. 1978;93:62-66.
Mosteller R.D. Simplified calculation of BSA. Letter. N. Engl. J. Med.. 1987;317(17):1098.
NMC. Standards for medicines management. London: Nursing and Midwifery Council, 2008.
NMC. The code: standards of conduct, performance and ethics for nurses and midwives. London: Nursing and Midwifery Council, 2008.
Wang Y., Moss J., Thisted R. Predictors of BSA. J. Clin. Anesth.. 1992;4(1):4-10.
Wright K. Drug calculations part 1: a critique of the formula used by nurses. Nurs. Stand.. 2008;22(36):40-42.
Wright K. Drug calculations part 2: alternative strategies to the formula. Nurs. Stand.. 2008;22(37):42-44.