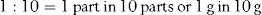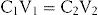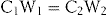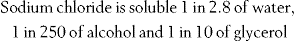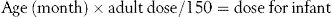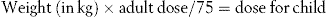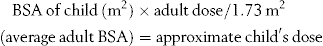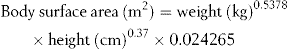Chapter 26 Pharmaceutical calculations
There are examples and self-assessment questions and answers provided to help you assess your progress.
Introduction
Many pharmacy students approach the calculations involved in dispensing and manufacturing with trepidation. There is no need. Most calculations are simple arithmetic. It is true that there are many steps in the dispensing process where things can go wrong and calculating quantities is one of them. However, careful, methodical working will minimize the risk of errors. Always try to relate the calculation to practice, visualize what you are doing and double-check everything.
How to minimize errors
As in all dispensing procedures, an organized, methodical approach is essential:
Expressions of concentration
The metric system is the International System of Units (SI Units) for weight, volume and length. The basic unit for weight is the kilogram (kg) while the basic unit for volume is the litre (L) and the basic unit of length is the metre (m). Appendix 3 gives information about the weights and measures commonly used in pharmacy. The prefix ‘milli’ indicates one-thousandth (10−3) and ‘micro’ one-millionth (10−6).
In some countries, the avoirdupois (or imperial) system (pounds and ounces) is still used in commerce and daily life. The imperial system of volume (pints and gallons) is still a common system for commerce and household measurement. Pharmacists need to know about these systems in order to avoid serious errors in interpretation of prescriptions. It is important to be able to change between the systems. Some conversion factors for the metric, avoirdupois and apothecary systems are shown in Box 26.1 (Examples 26.1-26.3).
Example 26.1
A prescription is received for a dose of 30 grains of a drug. How many grams is the dose?
Example 26.2
If 60 minims make 1 fluid drachm, and 8 fluid drachms make 1 fluid ounce, what is the volume of 1 minim in the metric system?
1 minim = 30/480 mL
Example 26.3
Sulfacetamide eye drops contain 200 drops in a 10 mL bottle. Calculate the volume of 1 drop.
Expressions of strength
Ratio is the relative magnitude of two like quantities. Thus:
If 1 g of sucrose is in 10 g of solution, the ratio is 1 : 10. Therefore, 10 g of sucrose is in 100 g of solution. This can be expressed as a percentage, so it is equivalent to a 10% w/w (weight in weight) solution.
Ratio strength is the expression of a concentration by means of a ratio, e.g. 1 : 10. Percentage strength is a ratio of parts per hundred, e.g. 10% (Examples 26.4-26.6).
Percentage weight in weight (w/w)
Percentage weight in weight (w/w) is the number of grams of an active ingredient in 100 grams (solid or liquid) (Example 26.7).
Percentage weight in volume (w/v)
Percentage weight in volume (w/v) is the number of grams of an active ingredient in 100 mL of liquid (Example 26.8).
Percentage volume in volume (v/v)
Percentage volume in volume (v/v) indicates the number of millilitres (mL) of an active ingredient in 100 mL of liquid (Example 26.9).
Miscellaneous examples
Example 26.10
Express 30 g of dextrose in 600 mL of solution as a percentage, indicating w/w, w/v or v/v.
Example 26.11
What is the percentage of magnesium carbonate in the following syrup?
| Magnesium carbonate | 15 g |
| Sucrose | 820 g |
| Water, q.s. | to 1000 mL |
Percentage is the number of grams of magnesium carbonate in 100 mL of syrup.
Example 26.12
Calculate the amount of drug in 5 mL of cough syrup if 100 mL contains 300 mg of drug.
Example 26.13
Compute the percentage of the ingredients in the following ointment (to 2 decimal places):
| Liquid paraffin | 14 g |
| Soft paraffin | 38 g |
| Hard paraffin | 12 g |
To find the amounts of the ingredients in 100 g of ointment, each figure will be multiplied by 100/64:
It is useful to double-check that these numbers add up to 100% (allowing for the rounding off to 2 decimal places).
Moles and molarity
Concentrations can also be expressed in moles or millimoles (see also Ch. 38). When a mixture contains the molecular weight of a drug in grams in 1 litre of solution, the concentration is defined as a 1 molar solution (1 mol). It has a molarity of 1. Thus, for example, the molecular weight of potassium hydroxide (KOH) is the sum of the atomic weights of its elements, i.e. KOH = 39 + 16 + 1 = 56. Therefore a 1 molar solution (1 mol) of KOH contains 56 g of KOH in 1 litre of solution.
A 1 millimole (mmol) solution of KOH contains one-thousandth of a mole in 1 litre = 56 mg (Examples 26.14-26.16).
Example 26.14
Calculate the number of moles (molarity) of a solution if it contains 117 g of sodium chloride (NaCl) in 1 L of solution (atomic weights: Na = 23, Cl = 35.5).
Calculating quantities from a master formula
In extemporaneous dispensing, a list of the ingredients is provided on the prescription or is obtained from a recognized reference source where the quantities of each ingredient are indicated. It may be that this ‘formula’ is for the quantity requested, but more often the quantities provided by the master formula have to be scaled up or down, depending on the quantity of the product required. This can be achieved using proportion or by deriving a ‘multiplying factor’. The latter is the ratio of the required quantity divided by the formula quantity. The following examples illustrate this process (Examples 26.17 and 26.18).
Example 26.17
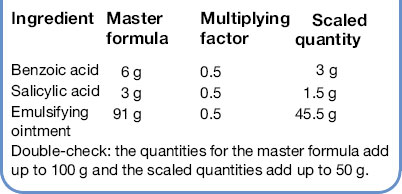
Calculate the quantities to prepare the following prescription:
The master formula is for 100 g, the prescription is for 50 g, therefore the multiplying factor is 50/100, i.e. each quantity in the master formula is multiplied by 50/100 = 0.5 to give the scaled quantity.
Double-check: the quantities for the master formula add up to 100 g and the scaled quantities add up to 50 g.
Example 26.18
You are requested to dispense 200 mL of Ammonium Chloride Mixture BPC. The formula can be found in a variety of reference books such as Martindale. In this example the master formula gives quantities sufficient for 10 mL. As the prescription is for 200 mL, the multiplying factor is 200/10. Thus the quantity of each ingredient in the master formula has to be multiplied by 20 to provide the required amount.
| Ingredient | Master formula | Scaled quantity |
| Ammonium chloride | 1 g | 20 g |
| Aromatic solution of ammonia | 0.5 mL | 10 mL |
| Liquorice liquid extract | 1 mL | 20 mL |
| Water | to 10 mL | to 200 mL |
Because this formula contains a mixture of volumes and weights it is not possible to calculate the exact quantity of water which is required. However, it is always good practice to have an idea of what the approximate quantity will be. The liquid ingredients of the preparation, other than the water, add up to 30 mL and there is 20 g of ammonium chloride. The volume of water required will therefore be between 150 mL and 170 mL.
In most formulae where a combination of weights and volumes is required, the formula will indicate that the preparation is to be made up to the required weight or volume with the designated vehicle. However, occasionally, as can be seen in the next example, a combination of stated weights and volumes is used and it is not possible to indicate what the exact final weight or volume of the preparation will be. In these instances an excess quantity is normally calculated for and the required amount measured (Example 26.19).
Example 26.19
Calculate the quantities required to produce 300 mL Turpentine Liniment BP 1988.
| Ingredient | Master formula |
| Soft soap | 75 g |
| Camphor | 50 g |
| Turpentine oil | 650 mL |
| Water | 225 mL |
When the total number of units is added up for this formula it comes to 1000. However, because it is a combination of solids and liquids, it will not produce 1000 mL. The prescription is for 300 mL and experience shows that calculating for 340 units will provide slightly more than 300 mL. The required amount can then be measured.
| Ingredient | Master formula | Scaled quantity for 340 units |
| Soft soap | 75 g | 25.5 g |
| Camphor | 50 g | 17 g |
| Turpentine oil | 650 mL | 221 mL |
| Water | 225 mL | 76.5 mL |
Calculations involving parts
In the following example the quantities are expressed as parts of the whole. The number of parts is added up and the quantity of each ingredient calculated by proportion or multiplying factor, to provide the correct amounts (Example 26.20).
Example 26.20
The quantity which is to be prepared of the following formula is 60 g.
| Ingredient | Master formula | Quantity for 60 g |
| Zinc oxide | 12.5 parts | 7.5 g |
| Calamine | 15 parts | 9 g |
| Hydrous wool fat | 25 parts | 15 g |
| White soft paraffin | 47.5 parts | 28.5 g |
The total number of parts adds up to 100 so the proportions of each ingredient will be 12.5/100 of zinc oxide, 15/100 of calamine and so on. The required quantity of each ingredient can then be calculated. Zinc oxide 12.5/100 of 60 g, calamine 15/100 of 60 g, etc. as indicated above.
There are some situations when extra care is necessary in reading the prescription (Example 26.21).
Example 26.21
Two products are to be dispensed:
| Betnovate® cream | 1 part |
| Aqueous cream | to 4 parts |
| Prepare 50 g | |
| Haelan® ointment | 1 part |
| White soft paraffin | 4 parts |
| Prepare 50 g | |
At first glance these calculations look similar but the quantities required for each are different. In the Betnovate prescription the total number of parts is 4, i.e. 1 part of Betnovate and 3 parts of aqueous cream to produce a total of 4 parts. However, in the Haelan prescription the total number of parts is 5, i.e. 1 part of Haelan ointment and 4 parts of white soft paraffin.
The quantities required for the prescriptions are as follows:
| Betnovate® cream | 12.5 g |
| Aqueous cream | 37.5 g |
| Haelan® ointment | 10 g |
| White soft paraffin | 40 g |
Calculations involving percentages
There are conventions which apply when dealing with formulae which include percentages:
In the following example a liquid ingredient, the coal tar solution, is stated as a percentage and a weight in grams of final product is requested. The convention of % w/w is applied (Example 26.23).
Example 26.22
Prepare 500 g of the following ointment
| Ingredient | Master formula | Quantity for 500 g |
| Sulphur 2% | 0.2 g | 10 g |
| Salicylic acid 1% | 0.1 g | 5 g |
| White soft paraffin to 10 g | to 10 g | 485 g (to 500 g) |
The master formula is for a total of 10 g. To calculate the quantities required for 500 g the multiplying factor for each ingredient is 500/10 = 50. Remember do not multiply the percentage figure. This always remains the same no matter how much is being prepared.
Example 26.23
The quantity to be made is 30 g.
| Ingredient | Master formula | Quantity for 30 g |
| Coal tar solution 3% | 3 g | 0.9 g |
| Zinc oxide 5 g | 5 g | 1.5 g |
| Yellow soft paraffin to 100 g | 92 g | 27.6 g |
When dealing with preparations where ingredients are expressed as a percentage concentration it is important to check that the standard conventions apply because there are some situations where they do not apply. Two examples are given below:
This means that when preparing Syrup BP the appropriate weight of sucrose is weighed out and water is added to the required weight, not volume.Changing concentrations
Sometimes it is necessary to increase or decrease the concentration of a medicine by the addition of more drug or a diluent. On other occasions, instructions have to be provided to prepare a dilution for use. These problems can be solved by the dilution equation:
where C1 and V1 are the initial concentration and initial volume respectively; and C2 and V2 are the final concentration and final quantity of the mixture respectively.
When three terms of the equation are known, the fourth term can be made the subject of the formula, and solved (Examples 26.24-26.27).
Example 26.24
What is the final concentration if 60 mL of a 12% w/v chlorhexidine solution is diluted to 120 mL with water?
Example 26.25
What concentration is produced when 400 mL of a 2.5% w/v solution is diluted to 1500 mL (answer to 2 decimal places)?
Example 26.27
What percentage of atropine is produced when 200 mg of atropine powder is made up to 50 g with lactose as a diluent?
The atropine powder is a pure drug, so its concentration (C1) is 100% w/w. The initial weight of the atropine powder (W1) = 200 mg = 0.2 g. Therefore, we can modify the dilution equation to read:
where C2 and W2 are the final concentration and final weight respectively, of the diluted drug. The diluting medium is the lactose.
Alligation
Alligation is a method for solving the number of parts of two or more components of known concentration to be mixed when the final desired concentration is known. When the relative amounts of components must be calculated for making a mixture of a desired concentration, the problem is most easily solved by alligation (Examples 26.28 and 26.29).
Example 26.28
Calculate the amounts of a 2% w/w metronidazole cream and of metronidazole powder required to produce 150 g of 6% w/w metronidazole cream (to 2 decimal places).
In alligation, the two starting material concentrations are placed above each other on the left hand side of the calculation. The target concentration is placed in the centre. The arithmetic difference between the starting material and the target is calculated and the answer recorded on the right hand end of the diagonal. The proportions of the two starting materials are then given by reading horizontally across the diagram.
As shown above, the difference between the concentration of the pure drug powder (100%, recorded top left) and the desired concentration (6%) is 94 (recorded bottom right). This is equivalent to the number of parts of 2% cream required (read horizontally across the bottom). Similarly, the difference between the concentration of 2% cream (recorded bottom left) and the desired concentration (6%) is 4 (recorded top right). This is equivalent to the number of parts of 100% drug (metronidazole powder) needed for the mixture (read horizontally across the top).
The total amount (4 parts + 94 parts = 98 parts) is 150 g.
Therefore, the amount of 2% cream required = 94 parts × 150/98 g = 143.88 g.
The amount of pure metronidazole (100%) required = 4 parts × 150/98 = 6.12 g.
Example 26.29
Promazine oral syrup is available as 25 mg/5 mL and 50 mg/5 mL. Calculate the quantities to use to prepare 150 mL of 40 mg/5 mL of the oral syrup.
Convert all the concentrations to percentages.
Therefore, 25 mg/5 mL is equivalent to 0.025 g in 5 mL = 0.500 g in 100 mL = 0.5% w/v.
Similarly, 50 mg/5 mL = 1% w/v; and 40 mg/5 mL = 0.8% w/v.
Total number of parts
Amount of 50 mg/5 mL (1.0% w/v) oral syrup needed Amount of 25 mg/5 mL (0.5% w/v) oral syrup neededCalculations where quantity of ingredients is too small to weigh or measure accurately
When preparing medicines by extemporaneous dispensing, the quantity of active ingredient required may be too small to weigh or measure with the equipment available. In these situations a measurable quantity has to be diluted with an inert diluent. The process is called ‘trituration’ (see Ch. 35).
Small quantities in powders
The method for preparing divided powders is described in Chapter 35 (Example 26.30).
Example 26.30
Calculate the quantities required to make 10 powders each containing 200 micrograms of digoxin.
Assume that the balance available has a minimum weighable quantity of 100 mg. An inert diluent, in this case lactose, will be used for the trituration. The convenient weight of each divided powder is 120 mg.
The total weight of powder mixture required will be 10 × 120 = 1200 milligrams = 1.2 g.
| Digoxin | 2 mg |
| Lactose | 1198 mg |
| Total | 1200 mg |
The weight of digoxin is too small to weigh. The minimum weighable quantity of 100 mg is weighed and used in the triturate. A 1 in 10 dilution is produced.
Trituration A
| Digoxin | 100 mg |
| Lactose | 900 mg |
| Total | 1000 mg |
Each 100 mg of this mixture (A) contains 10 mg of digoxin.
Small quantities in liquids
If the quantity of a solid to be incorporated into a solution is too small to weigh, again dilutions are used. In this case a solution is prepared, so the solubility of the substance needs to be considered. Normally a 1 in 10 or 1 in 100 dilution is used (Example 26.31).
Example 26.31
Calculate the quantities required to prepare 100 mL of a solution containing 2.5 mg morphine hydrochloride/5 mL.
| Morphine hydrochloride | 50 mg |
| Chloroform water | to 100 mL |
The solubility of morphine hydrochloride is 1 in 24 of water.
The minimum quantity of 100 mg of morphine hydrochloride is weighed and made up to 10 mL with chloroform water (this weight of morphine hydrochloride will dissolve in 2.4 mL).
5 mL of this solution (A) provides the 50 mg of morphine hydrochloride required.Take 5 mL of solution A and make up to 100 mL with chloroform water.
Solubilities
When preparing pharmaceutical products, the solubility of any solid ingredients should be checked. This will give useful information on how the product should be prepared. Examples of the calculations are given in Chapters 25 and 30. The objective of this section is to clarify the terminology used when solubilities are stated.
The solubility of a drug can be found in reference sources such as the drug monograph in Martindale. The method of stating solubilities is as follows:
This means that 1 g of sodium chloride requires 2.8 mL of water, 250 mL of alcohol or 10 mL of glycerol to dissolve it. An example of how knowledge of a substance’s solubility can help in extemporaneous dispensing can be found in Chapter 25. Some examples of calculating quantities of liquids required to dissolve solids are found in the self-assessment section (questions 6.1–6.4) at the end of this chapter.
Calculations involving doses
A simple calculation which pharmacists sometimes have to make while dispensing is to calculate the number of tablets or capsules or volume of a liquid medicine to be dispensed (Examples 26.32 and 26.33).
Example 26.32
The doctor prescribes orphenadrine tablets, 100 mg to be taken every 8 hours for 28 days. Orphenadrine is available as 50 mg tablets. How many tablets should be supplied?
For each dose, 2 tablets are required. Every eight hours means 3 doses per day.
Therefore, the total number of tablets required is 2 × 3 × 28 = 168 tablets.
Example 26.33
The following prescription is received:
Sodium valproate oral solution:
100 mg to be given twice daily for 2 weeks.
Sodium valproate oral solution contains sodium valproate 200 mg/5 mL.
This prescription is therefore translated as:
2.5 mL to be given twice daily for 2 weeks.
Calculating doses
An overdose of a drug, if given to a patient, can have very serious consequences and may be fatal. It is the responsibility of everyone involved in supplying or administering drugs to ensure that the accuracy and suitability of the dose are checked. The following are some examples of areas where errors can occur.
The standard way to check whether a drug dose is appropriate is to consult a recognized reference book. One of the commonest used for this purpose is the British National Formulary (BNF). When first using any reference source it is important to be aware of the terminology used, to avoid misinterpreting the entries, especially where doses are quoted as ‘x milligrams daily, in divided doses’. An explanation of the terminology will usually be given in the introduction to the book (Example 26.34).
Example 26.34
The following prescription is received:
There are a variety of doses quoted for verapamil in the BNF depending on the condition being treated. They are as follows for oral administration:
The dose given for hypertension is stated in a significantly different way. Whereas the other doses can be given three times daily, indicating a maximum of 360 mg in any one day, the hypertension dose is the total to be given in any one day and is divided up and given at the stated frequencies, i.e. a maximum of 240 mg, given twice daily or a maximum of 160 mg, given three times daily.
The prescription is for a dose higher than recommended, so consultation with the prescriber would be required. Be alert – variation in terminology and a lack of awareness could have very serious consequences.
Calculations of children’s doses
Children often require different doses from those of adults. Ideally these should be arrived at as a result of extensive clinical studies, although this is often not possible. When this is the case an estimate of the dose has to be made. This is best carried out using body weight (see next section), but where this is not available, there are three formulas which relate the child’s dose to the adult dose.
Calculation of doses by weight and surface area
For some drugs the amount of drug has to be calculated accurately for the particular patient. This is normally carried out using either body weight or body surface area. When body weight is being used, the dose will be expressed as mg/kg. In countries which still use pounds, it will be necessary to convert the patient’s weight in pounds into kilograms by dividing by 2.2. The total dose required is then obtained by multiplying the weight of the patient by the dose per kilogram.
Body surface area is a more accurate method for calculating doses and is used where extreme accuracy is required. This is necessary where there is a very narrow range of plasma concentration between the desired therapeutic effect and severe toxicity, such as with the drugs used to treat cancer. The body surface area can be calculated from body weight and height using the equation given below, but it is more usual to use a nomogram for its determination. The actual nomogram is published in many reference sources.
Reconstitution and infusion
Some drugs are not chemically stable in solution and so are supplied as dry powders for reconstitution just before use. Many of these are antibiotics, but there is also a range of chemotherapeutic agents used in cancer treatment. The antibiotics may be for oral use or for injection. An oral antibiotic for reconstitution comes as a powder in a bottle with sufficient space to add the water. The powder itself will remain stable for up to 2 years when dry. When reconstituted, a shelf life of 10–14 days is normal, depending on whether it is refrigerated or not. Those for injection are equally stable when dry, but are intended to be used within hours of reconstitution. Because they are for injection they are sterile powders and are dissolved in sterile water aseptically (see Ch. 29). There are a number of calculations which may be required around the reconstitution processes (Example 26.35).
Example 26.35
What dose of antibiotic will be contained in a 5 mL spoonful when a bottle containing 5 g of penicillin V is reconstituted to give 200 mL of syrup?
For this type of calculation, the simple proportion equation can be used:
Sometimes, the doctor may request a more or less concentrated syrup to be produced which requires altering the amount of water added from that indicated by the manufacturer (Example 26.36).
Example 26.36
We have an ampicillin product for reconstitution. It contains 2.5 g of ampicillin to be made up to 100 mL. To what volume should it be made to give 100 mg per 5 mL dose?
The normal mixture will give a dose of:
To calculate the amount of water to add, the same equation is used:
However, this type of oral mixture is likely to have other ingredients – thickeners, colours, flavours, etc. – which will occupy some of the final volume. So this may not be correct and we need to be able to calculate exactly how much water to add (Examples 26.37 and 26.38).
Example 26.37
The label on an ampicillin bottle indicates that 78 mL of water must be added to produce 100 mL of final syrup. How much water must be added to give the 125 mL final volume?
Therefore, the volume to add to give 125 mL is:Example 26.38
A child weighing 60 lb requires a dose of 8 mg/kg of ampicillin. Given that a 5 mL dose is to be given, what volume of water must be added when the powder is reconstituted? Instructions on the label indicate that dilution to 150 mL (by adding 111 mL) gives 250 mg ampicillin per 5 mL.
Therefore, volume to be added:
Drugs for injection solutions do not normally contain ingredients other than the drug (or they make an insignificant contribution to the final volume). However, they are usually packed as a quantity of drug with the final volume left to be calculated by the pharmacist (Example 26.39).
Example 26.39
Calculate the amount of sterile water to be added to a vial containing 200 000 units of penicillin G in order to produce a solution containing 40 000 units per millilitre.Again, simple proportion is used:
Calculation of infusion rates
Drugs may be given to patients intravenously by adding them to an intravenous (IV) infusion (see Ch. 38). Calculations involve working out how much drug solution should be added, working out how fast, in terms of mL/min, the infusion should be administered, and calculating what this means in terms of ‘drops per minute’ through the giving set. When an infusion pump is used, this can be set to deliver a specified number of mL/min. The final stage of drops/min is only required for traditional IV ‘drips’ (see Ch. 38) (Example 26.40).
Example 26.40
An ampoule of flucloxacillin contains 250 mg of powder with instructions to dissolve it in 5 mL of water for injections. What volume of this solution should be added to 500 mL of saline infusion to provide a dose of 175 mg?
Therefore, we require: 175 mg/50 mg/mL = 3.5 mL.
When administering intravenous infusions, the rate of addition is first calculated in terms of millilitres per minute (Example 26.41).
Example 26.41
100 mg of phenylephrine hydrochloride are added to 500 mL of saline infusion. What should be the rate of infusion to give a dose of 1 mg per minute? How long will the infusion take?
Using simple proportion: 100 mg/1 mg = 500 mL/y mL
y = 5 mL and contains the required amount of drug
The infusion rate should be 5 mL per minute.
The total volume is 500 mL, therefore the time taken at 5 mL/min is:
Most infusions are administered using a giving set with a dropping device on the tube (called venoclysis set; see Ch. 38). Partial clamping of the tube can be used to adjust the rate of dropping. Depending on the drop size – that is the number of drops per millilitre – it is then possible to convert a rate of millilitres per minute into drops per minute which the nurse can adjust (Example 26.42).
Example 26.42
A doctor requires an infusion of 1000 mL of 5% dextrose to be administered over an 8 hour period. Using an IV giving set which delivers 10 drops/mL, how many drops per minute should be delivered to the patient?
First convert the time into minutes:
A variation on this is when the doctor wishes a drug solution to be added to the infusion (Example 26.43).
Example 26.43
20 mL of a drug solution is added to a 500 mL infusion solution. It has to be administered to the patient over a 5 hour period. Using a set giving 15 drops per millilitre, how many drops per minute are required?
Then calculate the number of drops which will be administered in total: The duration of the infusion is to be: Calculate how many drops are required per minute:Self-assessment questions
(Express answers to 2 decimal places where appropriate.)
| Hydrocortisone | 10 g |
| Oxytetracycline | 30 g |
| Wool fat | 100 g |
| White soft paraffin | 860 g |
| a | White beeswax | 20 g |
| Hard paraffin | 30 g | |
| Cetostearyl alcohol | 50 g | |
| Soft paraffin | 900 g | |
| Prepare | 150 g | |
| b | Light magnesium carbonate | 3 g |
| Sodium bicarbonate | 5 g | |
| Aromatic cardamom tincture | 3 mL | |
| Chloroform water, double strength | 50 mL | |
| Water | to 100 mL | |
| Send | 120 mL | |
| a | Ichthammol | 5 parts |
| Cetostearyl alcohol | 3 parts | |
| Wool fat | 10 parts | |
| Zinc cream | to 100 parts | |
| Send | 120 g | |
| b | Chlorhexidine gluconate 20% solution | 5 parts |
| Cetomacrogol emulsifying wax | 25 parts | |
| Liquid paraffin | 10 parts | |
| Water | to 100 parts | |
| Send | 30 g | |
| c | Zinc oxide | 6 parts |
| Arachis oil | 7 parts | |
| Wool fat | 2 parts | |
| Water | to 20 parts | |
| Send | 60 g | |
| d | Wool alcohols | 6% |
| Soft paraffin | 10% | |
| Hard paraffin | 24% | |
| Liquid paraffin | 60% | |
| Send | 30 g | |
| e | Menthol | 2% |
| Eucalyptus oil | 10% | |
| Light magnesium carbonate | 7% | |
| Water | to 100% | |
| Send | 150 mL | |
| f | Cetrimide | 3% |
| Cetostearyl alcohol | 13.5 g | |
| White soft paraffin | 25 g | |
| Liquid paraffin | to 50 g | |
| Send | 150 g | |
| g | Starch | 7 parts |
| Zinc oxide | 8 parts | |
| Olive oil | 2 parts | |
| Wool fat | 3 parts | |
| Send | 30 g | |
| h | Cetomacrogol emulsifying wax | 60 g |
| Benzyl alcohol | 3 g | |
| Methyl paraben | 2.3% | |
| Water | to 200 g | |
| Send | 40 g | |
| i | Cetrimide | 3% |
| Cetostearyl alcohol | 13.5 g | |
| White soft paraffin | 25 g | |
| Liquid paraffin | to 50 g | |
| Send | 40 g | |
Self-assessment answers
| 3.1 | Hydrocortisone | 0.5 g |
| Oxytetracycline | 1.5 g | |
| Wool fat | 5 g | |
| White soft paraffin | 43 g |
| 3.2a | White beeswax | 3 g |
| Hard paraffin | 4.5 g | |
| Cetostearyl alcohol | 7.5 g | |
| Soft paraffin | 135 g |
| 3.2b | Light magnesium carbonate | 3.6 g |
| Sodium bicarbonate | 6.0 g | |
| Aromatic cardamom tincture | 3.6 mL | |
| Chloroform water, double strength | 60 mL | |
| Water | to 120 mL |
| 3.3a | Ichthammol | 6 g |
| Cetostearyl alcohol | 3.6 g | |
| Wool fat | 12 g | |
| Zinc cream | to 120 g |
| 3.3.b | Chlorhexidine gluconate 20% solution | 1.5 g |
| Cetomacrogol emulsifying wax | 7.5 g | |
| Liquid paraffin | 3 g | |
| Water | to 30 g |
| 3.3c | Zinc oxide | 18 g |
| Arachis oil | 21 g | |
| Wool fat | 6 g | |
| Water | to 60 g |
3.3dWool alcohols1.8 gSoft paraffin3 gHard paraffin7.2 gLiquid paraffin18 g
| 3.3e | Menthol | 3 g |
| Eucalyptus oil | 15 mL | |
| Light magnesium carbonate | 10.5 g | |
| Water | to 150 mL |
| 3.3f | Cetrimide | 4.5 g |
| Cetostearyl alcohol | 40.5 g | |
| White soft paraffin | 75 g | |
| Liquid paraffin | 30 g |
| 3.3g | Starch | 10.5 g |
| Zinc oxide | 12 g | |
| Olive oil | 3 g | |
| Wool fat | 4.5 g |
| 3.3h | Cetomacrogol emulsifying wax | 12 g |
| Benzyl alcohol | 0.6 g | |
| Methyl paraben | 0.92 g | |
| Water | 26.48 g |
| 3.3i | Cetrimide | 1.2 g |
| Cetostearyl alcohol | 10.8 g | |
| White soft paraffin | 20 g | |
| Liquid paraffin | 8 g |