Introduction to: Inferential statistics
The statistical analysis of the data is an essential stage in the process of quantitative research. The principles of inferential statistics, as introduced in this section, are applied for deciding if the obtained sample data show the differences and patterns we set out to demonstrate in the population. This is the case for all types of research where we are using sample data to make inferences concerning populations.
Quantitative research in the health sciences mostly involves working with samples drawn from populations. In order to generalize our findings, we must draw generalizations and inferences from sample statistics (e.g. X–, s) to the population parameters (e.g. μ, σ). Inferences are always probabilistic, because even with random samples there is always the chance of sampling error. The finite probability of sampling error implies that the differences or patterns identified in our sample data could represent random variations or chance patterns rather than ‘real’ ones which are true for the population as a whole.
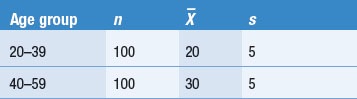
As an illustration, imagine that we have collected data in a study aimed at identifying age-related differences in the use of sedatives and tranquillizers in a given population. Our participants (n = 200) kept diaries over a period of 1 year, recording each time they had taken a sedative or tranquillizer. The research question is: is there a difference between sedative or tranquillizer use in older and younger people? Assume that the following hypothetical data were obtained:
Three important and interrelated questions are examined in Section 6 concerning the evidence provided by sample data such as those shown in the above table.
? For example, is it true that the mean tranquillizer intake for the 20–39 age group is μ = 20?The key issue here is that we are using sample data for decision making. Sampling error refers to the difference between sample statistics and the actual state of the population.
We cannot eliminate sampling error even with large and well-chosen samples. Rather, as outlined in Section 6, we can apply the principles of inferential statistics to calculate the probability of error. We then use this information to minimize the probability of making errors when we generalize from sample statistics to population parameters.
In Chapter 17 we examine how sampling distributions are derived and used for calculating the probability of obtaining a given sample statistic. This information can be applied to the calculation of confidence intervals, which represent a range of scores which contain the true population parameter at a given level or probability.
In Chapter 18 we outline the logic of hypothesis testing, using single sample z and t tests as exemplars. Hypothesis testing is a procedure used to decide if a difference or pattern identified in our sample data is statistically significant. If the outcome of our analysis is significant, then we are in a position to decide that the patterns or differences found in our data may be generalized to the populations from which the samples were drawn.
There are numerous statistical tests available for analysing the significance of our data. In Chapter 19 we discuss basic criteria for selecting an appropriate statistical test, including (i) scale of measurement used to collect the data, (ii) the number of groups being compared and (iii) the dependence or independence of measurements. We will use the χ2 (chi-squared) test to demonstrate how statistical tests are selected and used to analyse the data.
Ultimately, statistical decision making is probabilistic, implying that the possibility of making decision errors cannot be eliminated. Decisions may be correct, or involve what are called Type I and Type II errors. In Chapter 20, we examine how these errors may influence our interpretation of the obtained data in relation to the aims or hypotheses guiding our research, and we will examine strategies which can be employed to reduce the probability of making such errors. In this chapter we outline the relationship between effect size and the clinical or practical significance of research findings.